[技術解説]
確率・統計による真値推定技術「カルマン・フィルタ」


図2　［VOD/KIT］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門のサンプル動画 図3　プログラミング実習キット「カルマン倒立振子」

物理法則にもとづくモデルをマイコンに組み込んで操縦させる

1969年，アメリカ航空宇宙局 NASAは38万kmのかなたにある月に宇宙船「アポロ11号(写真1)」をコンピュータで誘導し，無事に着陸させることに成功しました．

アポロ11号のコンピュータ(写真2)は， わずか70行程度のプログラム を利用して宇宙船の位置や姿勢を正確に算出していました． 「数理モデル」と「実測値」を利用して確率統計処理によって雑音(誤差)を最小化し， 最も確からしい値を短時間で推定する「カルマン・フィルタ」です．

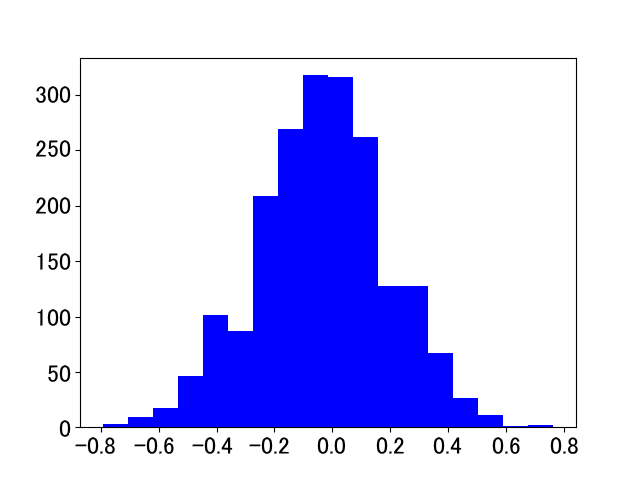
どんなセンサの値にも，「誤差」や「ゆらぎ」といった不要な成分が含まれています． センサの出力値の統計をとると，おおよそ図1のような「正規分布」が得られます． この正規分布の中心が「本当の値」すなわち「真値」であると考えられます．

たくさんのデータの平均をとれば「正規分布の中心」を求められそうですが， 実際のリアルタイム処理では図1のように大量のデータを実測するのは困難です． そこで確率・統計の考え方を利用して「真値」にアプローチしようというのが，カルマン・フィルタのアイディアです． カルマン・フィルタを利用すれば，少ないデータをもとにして短時間で「真値」を推定することができます．

アポロ11号が搭載したアルゴリズムは，いわゆるAI（人工知能）の原型ともいえるものです． 最近のAIには様々なアルゴリズムがありますが，その中でも教師データを読み込ませてニューラル・ネットワーク上に一種のモデルを構築するという方法がよく知られています． アポロ11号で用いられたカルマン・フィルタにも「計算モデル」は搭載されていましたが， それは自動的な学習によって生成されたものではなく，科学者が自ら用意した「物理モデル」でした． 宇宙船に組み込まれたカルマン・フィルタは，「手作業で作ったモデルにもとづいて確率的にもっとも正しそうな値を探すアルゴリズム」ということになります．

1969年当時のコンピュータは何億円もした大がかりなものでしたが，現在は数百円で遥かに高性能なワンチップ・マイコンが手に入ります． 今のワンチップ・マイコンを使えば，カルマン・フィルタの処理を十分高速に処理することができます． このキットはカルマン・フィルタによる処理を体験し，その動作原理を理解するために大いに役立ちます．

写真1: 1969年，NASAは，コンピュータ誘導によって，有人宇宙船「アポロ11号」38万km先にある月まで正確に誘導し着陸させた 写真2: アポロ11号に搭載された誘導用コンピュータ“AGC(Apollo Guidance Computer)” 図1: センサによる測定を何度も繰り返すと正規分布が得られる

カルマン・フィルタのアルゴリズム

カルマン・フィルタのアルゴリズムは，基本的に4本の数式で表されます． 本キットでは，この計算をマイコン上で実行してロボットの姿勢推定を行っています． 具体的なプログラム例は 本ページの末尾 に掲載しています． また，数学的な内容については ［VOD/KIT］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門にて詳しく解説しています．

（1）共分散行列の更新

\begin{equation} P_0 = \left(P_{0}^{\prime -1} -C^{T}W^{-1}C \right)^{-1} \end{equation}

（2）真値の推定値の計算

\begin{equation} \hat{\bm{x}}_0 = \tilde{\bm{x}}_0 + P_0 C^{T} W^{-1} \left( \bm{y}_0 -C \tilde{\bm{x}}_0 \right) \end{equation}

（3）1ステップ先の共分散行列の予測

\begin{equation} P_1^{\prime} = AP_0 A^{T} + BUB^{T} \end{equation}

（4）1ステップ先の予測値の計算

\begin{equation} \tilde{\bm{x}}_1 = A\hat{\bm{x}}_0 + B \bm{u}_0 \end{equation}

下記のソース・コードは，カルマン・フィルタの中核部分の抜粋です（ここでは全体としての計算量を減らすために「カルマン・ゲイン」を経由した計算を採用しています）． 本キットのマイコンでは，この計算を10 msecの周期（100回/秒）で実行しています． 

//---------------------------------------
//Kalman Filter (all system)
//---------------------------------------
//calculate Kalman gain: G = P'C^T(W+CP'C^T)^-1
mat_tran(C_x[0], tran_C_x[0], 4, 4);//C^T
mat_mul(P_x_predict[0], tran_C_x[0], P_CT[0], 4, 4, 4, 4);//P'C^T
mat_mul(C_x[0], P_CT[0], G_temp1[0], 4, 4, 4, 4);//CPC^T
mat_add(G_temp1[0], measure_variance_mat[0], G_temp2[0], 4, 4);//W+CP'C^T
mat_inv(G_temp2[0], G_temp2_inv[0], 4, 4);//(W+CP'C^T)^-1
mat_mul(P_CT[0], G_temp2_inv[0], G[0], 4, 4, 4, 4); //P'C^T(W+CP'C^T)^-1

//x_data estimation: x = x'+G(y-Cx')
mat_mul(C_x[0], x_data_predict[0], C_x_x[0], 4, 4, 4, 1);//Cx'
mat_sub(y[0], C_x_x[0], delta_y[0], 4, 1);//y-Cx'
mat_mul(G[0], delta_y[0], delta_x[0], 4, 4, 4, 1);//G(y-Cx')
mat_add(x_data_predict[0], delta_x[0], x_data[0], 4, 1);//x'+G(y-Cx')

//calculate covariance matrix: P=(I-GC)P'
mat_mul(G[0], C_x[0], GC[0], 4, 4, 4, 4);//GC
mat_sub(I4[0], GC[0], I4_GC[0], 4, 4);//I-GC
mat_mul(I4_GC[0], P_x_predict[0], P_x[0], 4, 4, 4, 4);//(I-GC)P'

//predict the next step data: x'=Ax+Bu
Vin = motor_value;
if(motor_value > vdd_voltage)

{
    Vin = vdd_voltage;
}
if(motor_value < -vdd_voltage)
{
    Vin = -vdd_voltage;    
}
mat_mul(A_x[0], x_data[0], A_x_x[0], 4, 4, 4, 1);//Ax_hat
mat_mul_const(B_x[0], Vin , B_x_Vin[0], 4, 1);//Bu
mat_add(A_x_x[0], B_x_Vin[0], x_data_predict[0], 4, 1);//Ax+Bu 

//predict covariance matrix: P'=APA^T + BUB^T
mat_tran(A_x[0], tran_A_x[0], 4, 4);//A^T
mat_mul(A_x[0], P_x[0], AP[0], 4, 4, 4, 4);//AP
mat_mul(AP[0], tran_A_x[0], APAT[0], 4, 4, 4, 4);//APA^T
mat_tran(B_x[0], tran_B_x[0], 4, 1);//B^T
mat_mul(B_x[0], tran_B_x[0], BBT[0], 4, 1, 1, 4);//BB^T
mat_mul_const(BBT[0], voltage_variance, BUBT[0], 4, 4);//BUB^T
mat_add(APAT[0], BUBT[0], P_x_predict[0], 4, 4);//APA^T+BUB^T

カルマン・フィルタの応用

カルマン・フィルタの有名な応用先としては，GPSを利用したナビゲーション・システムが挙げられます． さらに，自動車，船舶，飛行機など，自動運転(ADAS)の機能をもつほとんどの装置にはカルマン・フィルタが使われています． また，金融の分野における株価の予測や，土木の分野における自然災害の予測，天気予報などにも使われています．

最近は，「真値を推定する」という機能を利用して「手元の実測データから，実際には取得できないデータを求める」という使い方もされているようです． これは，いわゆるデータ・サイエンスや人工知能と呼ばれる分野と深い関わりがあります．

カルマン・フィルタはわれわれの生活のいたるところで利用されており，ほとんどすべての人が何らかの形でその恩恵を受けています．