故障推定から画像認識まで！
「主成分分析」による最高性能AIエッジ開発

R/Pythonで誰でもできるビッグ・データ処理

• 著者・講師：別府 伸耕/Nobuyasu Beppu (リニア・テック)
• 企画編集・主催： ZEPエンジニアリング株式会社


• 関連製品：［VOD］故障推定から画像認識まで！「主成分分析」による最高性能AIエッジ 開発入門
• 関連製品：［VOD/KIT］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門
• 関連記事：Pythonではじめる 数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
• 関連記事：Pythonではじめる 数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]

複雑かつ膨大なデータを一瞬で見抜く！ 「主成分分析」入門！

アメリカ大統領選挙のデータを題材にして主成分分析の威力を解説

「主成分分析」（principal component analysis: PCA）は，「多次元のデータを低次元に落とし込むテクニック」です．この解析手法を利用すれば，ビッグ・データの解析やパターン認識といったAI/IoT分野で重要となるデータ処理を簡単に実装することができます．

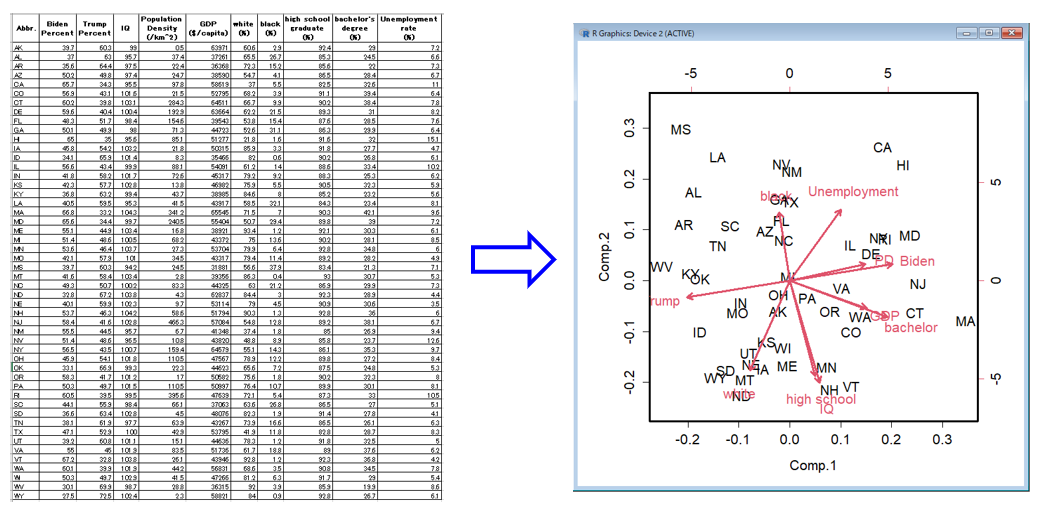
本セミナでは図1に示す「2020年アメリカ大統領選挙」のデータを題材にして主成分分析について解説します．解析の対象は，アメリカの50個の州に関する「大統領選挙の候補者の支持率」，「平均IQ」，「人口密度」，「1人あたりGDP」，「白人率」，「黒人率」，「学歴」，「失業率」といったデータです．このデータは膨大な情報を含むため，一見した限りではその内容を読み取れません．ところが，「主成分分析」によって図1のようなグラフを作れば，各項目どうしの関係性や各州の位置づけなどを瞬時に把握することができます．

エンジニアリングの分野でも強力なツールになる

主成分分析は先述のような統計的な社会調査に加えて，マーケティングなどにも大いに活用されています．さらには，各種信号処理やパターン認識といったエンジニアリングの分野とも非常に高い親和性をもちます．

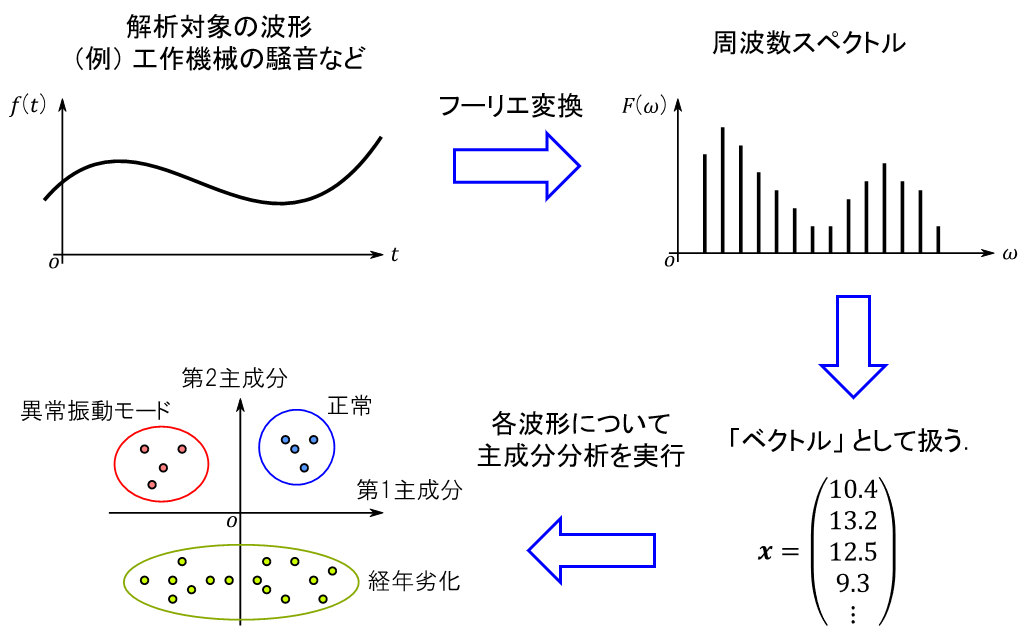
図2に示すのは，機器の振動などの測定波形にもとづいた「異常検出」に主成分分析を活用した例です．オシロスコープやデータ・ロガーなどで取得した波形に対してそのまま，あるいはフーリエ変換などを行って周波数領域に変換してから，主成分分析を実行します．主成分分析の結果は波形の特徴ごとにカテゴリライズされるので，あらかじめ「正常時」や「異常時」などのデータをとっておけば，今とった測定データの位置づけをもとにして状況を判断できます．

パターン認識にも応用できる

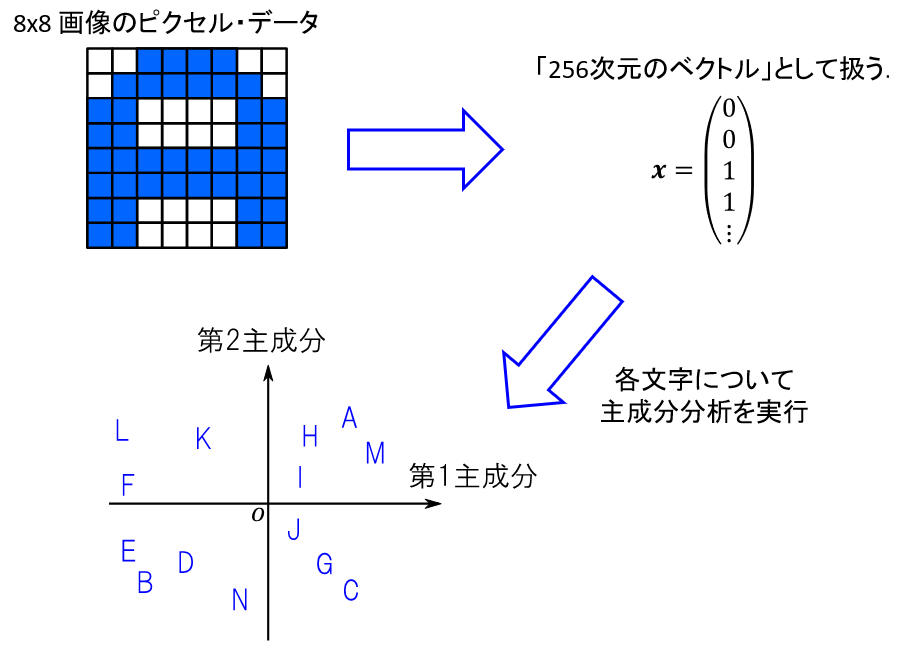
主成分分析は「データをカテゴライズする」ための手段として有用です．この特徴を活かせば，図3のような「パターン認識」を行うこともできます．実際にはパターン認識のためにいくつかのアルゴリズムを組み合わせる必要がありますが，主成分分析はその「前処理」として広く使われています．

入門編： お手軽な統計解析ツール“R”で主成分分析をやってみよう

本セミナでは2日間にわたって主成分分析の原理から応用までを解説します．内容をわかりやすくお伝えするために，「入門編」，「応用編」，「原理解説編」の3ステップに分けて説明を行います．

最初の「入門編」では，統計解析の実行環境である“R”を使って，とにかく主成分分析の威力を体感する目指します(図4)．Rにおける基本的なコマンド入力の方法から，主成分分析の実行方法，できあがったグラフの読み取り方などを解説します．

応用編： Pythonを使って自分でプログラムを書いてみよう

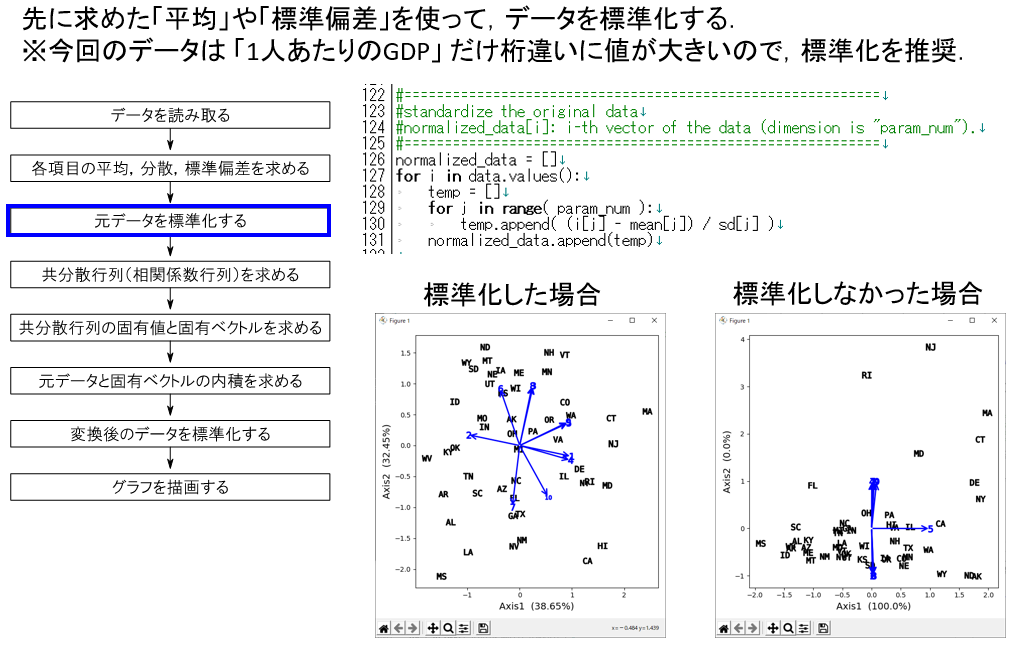
「応用編」では，主成分分析の具体的な計算手順（アルゴリズム）を解説します(図5)．“R”は手軽で良いのですが，具体的なアルゴリズムに対してはブラック・ボックスである感が否めません．細部まで計算処理を把握して統計解析を実行したいならば，やはり自分でプログラムを書いてしまうのが近道です．今回はプログラミング言語“Python”を利用した主成分分析のプログラム例を紹介します．

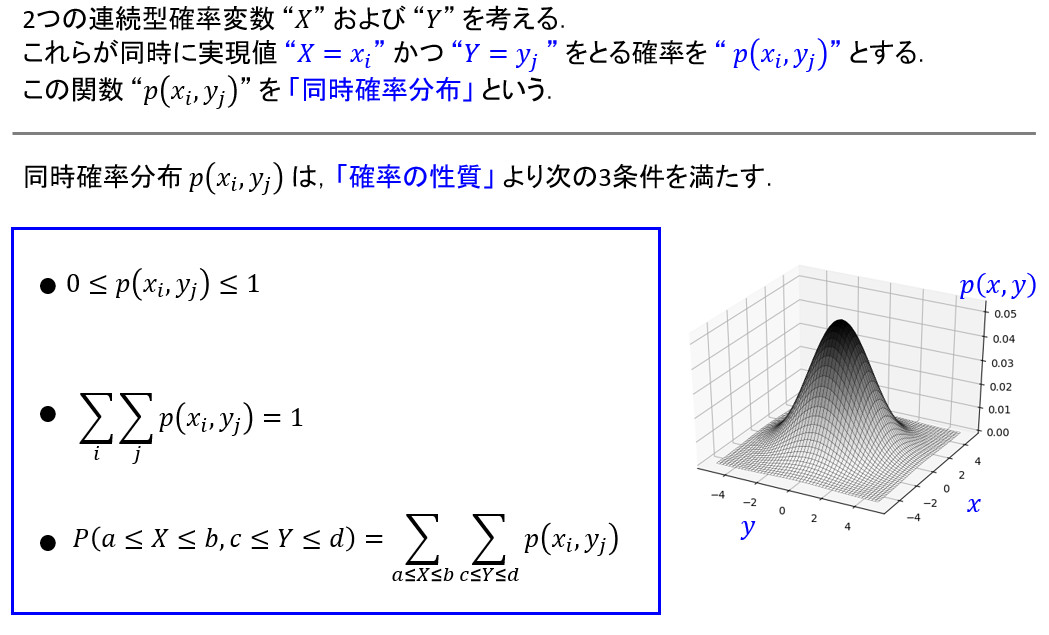
また，主成分分析のプログラムを書くためには，「期待値」や「共分散行列」といった用語を理解しておく必要があります．これらの用語は数学の「確率・統計」のものです．そこで，「応用編」では主成分分析を理解するために必要となる確率・統計の知識についても解説します(図6)．

原理解説編： 主成分分析のアルゴリズムを導出する

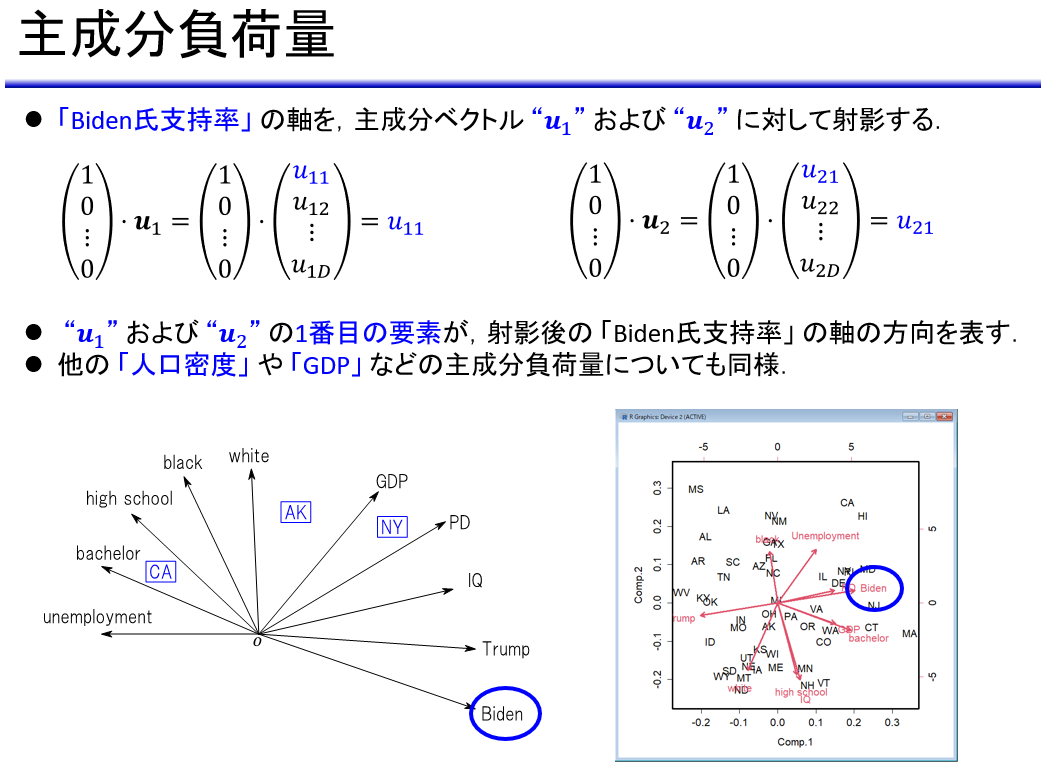
「原理解説編」では，主成分分析というアルゴリズムがどのようにして出来上がったのか，その原理的な部分まで踏み込んで解説します(図7)．

主成分分析のアルゴリズムを導出するためには，応用編で扱った「確率・統計」に加えて「微分・積分」および「線形代数」の知識が必要となります．これらの数学の知識は主成分分析にとどまらず，あらゆるエンジニアリングや統計解析の分野で必要となります．「原理解説編」ではそのための「基礎固め」をすべく，数学をとことんわかりやすく解説します．

「微分・積分」の内容としては，主に以下の内容を解説します．

• 微分・積分の使い道
• 1変数関数の微分
• 1変数関数の積分
• テイラー展開
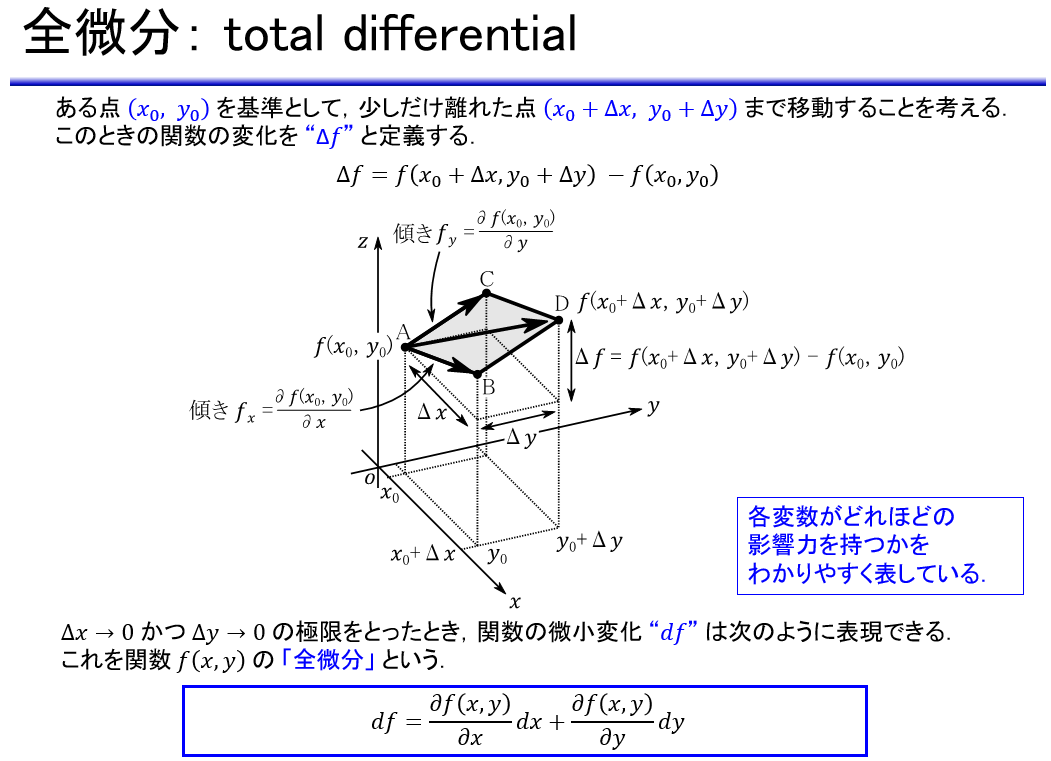
• 2変数関数の微分
• ラグランジュの未定乗数法

「線形代数」の内容としては，主に以下の内容を解説します(図8)．

• ベクトル
• 行列
• 固有値と固有ベクトル