パソコンでEMC対策！3大電磁界シミュレータの選び方

（1）有限要素法 FEM（2）モーメント法 MoM（3）有限差分時間領域法 FDTD

［Webinar/Book/data］AI×電磁界シミュレータによる高速&RF回路基板スピード設計（LIVE配信：7月28日，録画受講：7月29日～8月3日）

プリント基板設計や放射電磁界対策には，電磁界シミュレータは必須の存在です．設計検証や設計最適化に広く利用されています．

電磁界シミュレータと一口に言っても種類があり，長所と短所があります．電磁界シミュレータを賢く使うために，電磁界シミュレータの特徴を簡単に説明します．

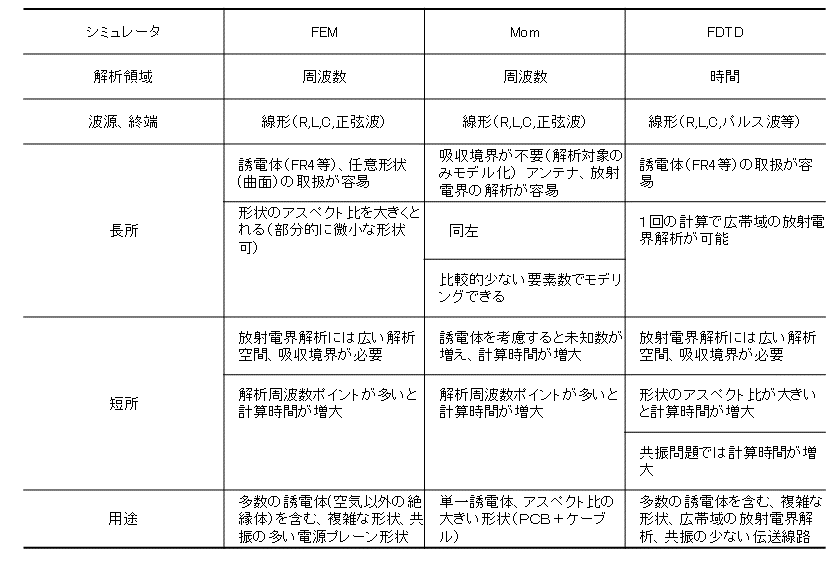
電磁界シミュレータには次のような種類があります（図1）．

FEMとMoMは周波数領域，FDTDは時間領域で計算します．

周波数領域の計算とは，正弦波に対する電磁界の応答を求めることです．基本的に定常状態の電磁界を計算します．横軸が周波数，縦軸が電磁界の状態です．

時間領域の計算とは，時間と電磁界の応答を求めることです．過渡応答がわかります．横軸が時間です．

いずれのシミュレータも，取り扱うことができる受動素子は，抵抗，キャパシタ，インダクタです．

周波数領域シミュレータの“FEM”や“MoM”は正弦波，時間領域シミュレータの“FDTD”は，パルス波形や任意形状の波形を取り扱うことができます．


図1　3大電磁界シミュレータとその特徴

電磁界シミュレータは，その計算方法により，得意，不得意がありますが，市販のシミュレータの多くは，短所を克服しているため，計算時間にも精度にも大差はありません．

FEMの長所は曲面や誘電体の取り扱いが容易で，部分的に小さい形状があっても計算時間は変化しません．

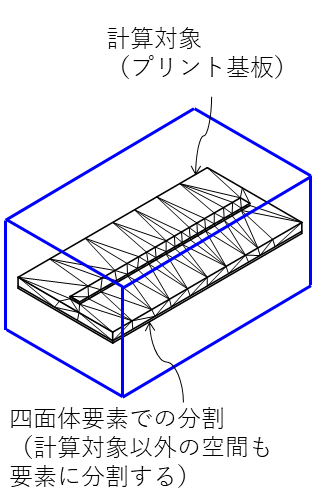
短所は，図2に示すように放射電界の計算には比較的広い解析空間が必要なこと，解析する周波数の数に比例して計算時間が長くなることです．

多数の誘電体を含む複雑な形状や共振が発生するような現象の計算に向いてします．プリント基板の電源面とグラウンド面のインピーダンスや放射電界の計算に適しています．


図2　FEM電磁界シミュレータと解析空間

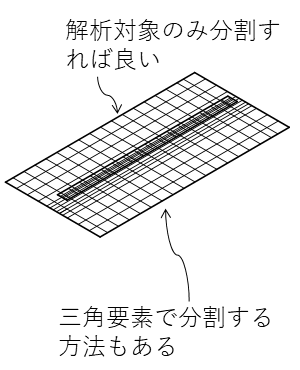
MoMの長所は，電流の流れる導体だけ分割すれば良く，何もない空間は分割する必要がありません（図3）．その結果，比較的少ない要素で解析対象をモデル化できます．

誘電体を含めた計算も可能ですが，未知数が増え，計算時間が増大します．またFEMと同様に計算する周波数の数が多いと，それに応じて計算時間が増えます．

解析対象が単一の誘電体を含む場合や，プリント基板にケーブルが接続されたようなアスペクト比が大きいモデルの解析に最適です．


図3　MoM電磁界シミュレータと解析空間

ESD（Electro Static Discharge）などの過渡現象を直接計算できます．

1回の計算で周波数領域のデータを広帯域に求めることができますが，共振が発生する現象では，計算時間が長くなります．理由は，共振現象が十分に収束後せずにフーリエ変換を利用して，時間領域から周波数領域に変換すると，変換誤差が大きくなるためです．

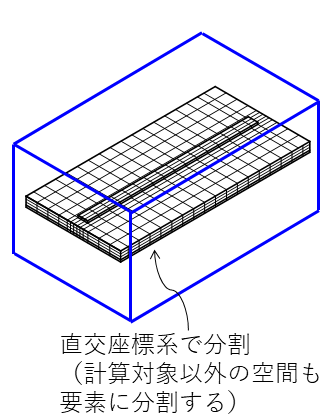
FEMと同様に，何もない空間も要素分割する必要があり，直交座標系で要素分割するため，曲面は階段近似になります（図4）．

誘電体の扱いが容易で，広帯域の$S$パラメータや放射電界を求めるのに適しています．


図4　FDTD電磁界シミュレータと解析空間

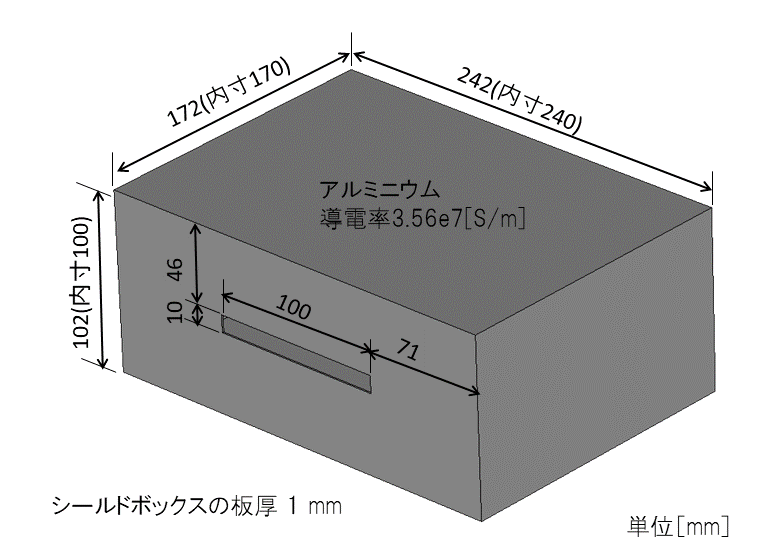
各シミュレータを使って，図5に示すシールド・ボックスからの放射電磁界を解析した結果を示します．

シールド・ボックスは内寸が$100 \times 240 \times 170$mm，厚さが1mmであり，素材はアルミです．$10 \times 100$mmの換気用のスリットが開いています．内部に，配線長が10mmのプリント基板があり，これがノイズ源です．

このモデルをFEM，MoM，FDTDで計算しました．FEMとMoMは異なるメーカのツールをそれぞれ2種類ずつ準備しました．


図5　シールド・ボックス・モデルでシミュレーションしてみる

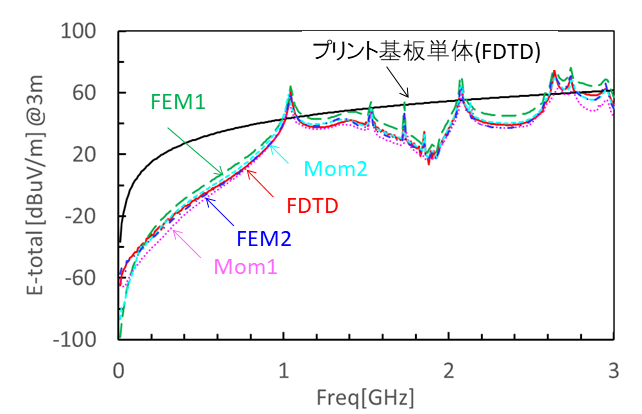
図6に各シミュレータの計算結果を示します．横軸は周波数，縦軸は3m遠方の放射電界です．黒色の実線は，プリント基板単体の放射電界です．

各シミュレータの計算結果は共振周波数も含めて良く一致しており，市販の電磁界シミュレータであれば，どれも同じ結果が得られることがわかります．ただし，解きたい問題によっては，向き不向きがあります．実際に計算してみることをお勧めします．


図6　シミュレーション結果