Pythonではじめる 数値解析入門
[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]

開発環境のセットアップから電磁界シミュレーションまで

• 著者・講師：別府 伸耕/Nobuyasu Beppu (リニア・テック)
• 企画編集・主催： ZEPエンジニアリング株式会社


• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
• 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
• 関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング 基礎編/応用編
• 関連製品：［VOD/KIT］実習キットでできる！ラズパイPicoでマイコン入門
• 関連製品：［VOD］故障推定から画像認識まで！「主成分分析」による最高性能AIエッジ 開発入門
• 関連製品：［VOD/KIT］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門
• 関連製品：［VOD/本］Pythonで一緒に！ロボット制御のモデルベース設計【状態フィードバック制御編】

• Vol.1　Pythonの開発環境をインストールする
• Vol.2　グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く

インデックス

本記事では，以下の項目に沿ってグラフ描画ライブラリ“Matplotlib”の基本的な使い方を解説します．

• グラフ描画ライブラリ“Matplotlib”の基礎知識
• グラフを描く時によく使う“NumPy”のノウハウ
• グラフの体裁を整える
• 散布図を描く
• 棒グラフを描く
• ヒート・マップを描く
• 等高線図を描く
• ベクトル場を描く
• 流線図を描く

グラフ描画ライブラリ“Matplotlib”の基礎知識

Matplotlibの概要

“Matplotlib”（マットプロットリブ）は，Python用のグラフ描画ライブラリです．有名な数値解析ソフトウェアである“MATLAB”（マトラボ）のグラフ描画（プロット）機能と同様の使い勝手を実現することを意識して開発されています．

MATLABは非常に多彩かつ高性能な数値計算機能を持ち，美しいグラフを手軽に描画することもできます．しかし，使用するためには（それなりに高額な）ライセンス料金を支払う必要があります．一方で，Matplotlibは基本的にグラフを描画する機能しか持ちませんが，オープン・ソースであり無償で使うことができます．

Matplotlib公式ドキュメント

本記事は，Matplotlibの公式ドキュメントを参考にして書いています．

特に，チュートリアルのページは初めてMatplotlibを使う場合を想定して書かれており，重要なポイントが簡潔にまとめられています．また，クラスやメソッドの詳細な仕様はAPIリファレンスにまとめられています．

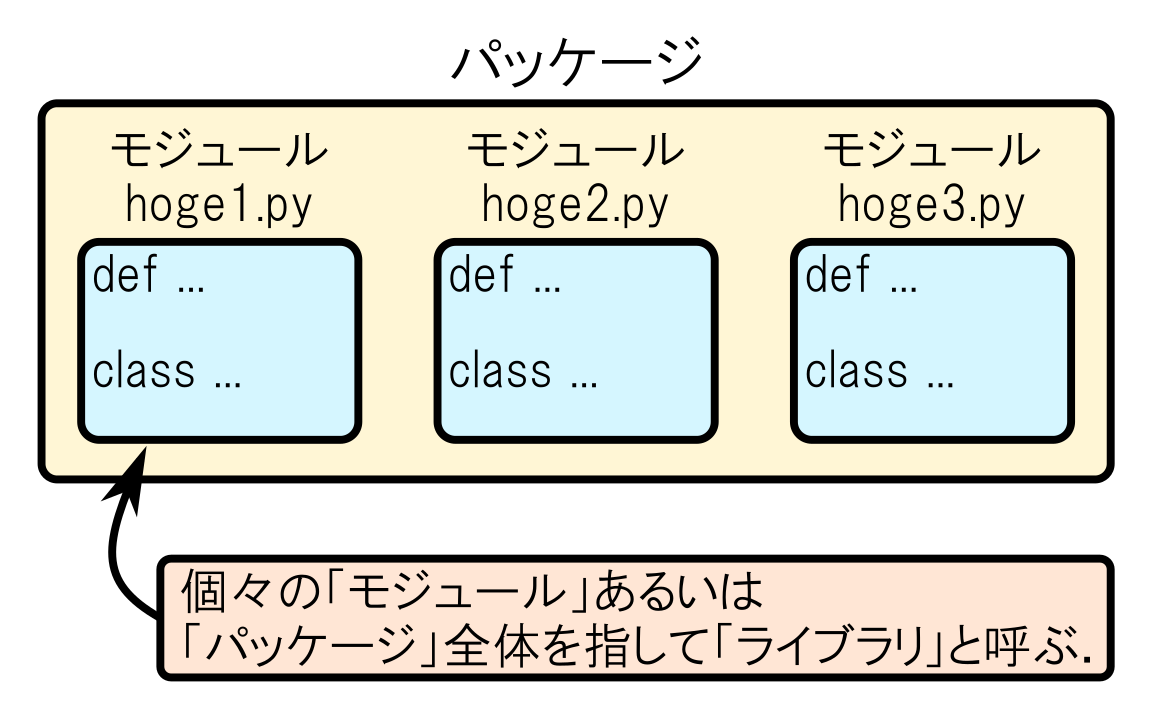
Pythonにおける「モジュール」，「パッケージ」，「ライブラリ」という用語

数値計算における本質的な話ではありませんが，Pythonで使う用語の確認です．

Pythonでは，一般に複数のクラスや関数をまとめたものを「モジュール」と呼びます．モジュールは，基本的に1つのPythonファイル（.py ファイル）と1対1で対応します．また，複数のモジュールをまとめたものを「パッケージ」と呼びます．パッケージは複数のPythonファイルを含むディレクトリ（フォルダ）を指すイメージです（図1）．

図1　Pythonにおける「モジュール」と「パッケージ」のイメージ

一般的なプログラミング言語では，汎用的に使うクラスや関数をまとめたものを「ライブラリ」と呼びます．Pythonの場合，「ライブラリ」という言葉が「モジュール」を指す場合もあれば「パッケージ」を指すこともあるようです．今後は，厳密に区別する必要が無い場合は「ライブラリ」と表記することにします．

Matplotlibのソース・コードは“site-packages”ディレクトリ内にある

Matplotlibのインストール・ディレクトリの内部を見れば，ライブラリの具体的な構造やソース・コードを確認することができます．一般的なPythonのライブラリ（Matplotlibも含む）は，Python本体のインストール・ディレクトリ（デフォルトならC:/Users/ユーザ名/AppData/Local/Programs/Python/Python**/）の中にある“Lib/site-packages/”というディレクトリに保存されています．なお，**にはPythonのバージョンを表す数字が入ります．

特に，後述の“pyplot”モジュール（“pyplot.py”というファイル）に定義されているクラスや関数に目を通しておくと，Matplotlibを扱う上で生じる疑問やトラブルを解決する上で大いに役立ちます．

“Matplotlib”と“NumPy”をあわせて使う

Pythonには，数値計算用の“NumPy”（ナンパイ）というライブラリが用意されています．これから作成するプログラムは，基本的に「NumPyの機能を使ってデータを計算し，そのデータをMatplotlibでグラフとして描画する」という流れになります．よって，リスト1のようにソース・コードの冒頭でMatplotlibとNumPyを読み込んでおきます．

import matplotlib.pyplot as plt
import numpy as np

我々がMatplotlibで利用するほぼすべての機能は，“pyplot”（パイプロット）というモジュールに定義されているクラスや関数を通して操作できます．よって，“matplotlib.pyplot”さえインポートしておけば実用上ほとんど困ることはありません．ただし，このままでは名前が長くて書きづらいので，“plt”という呼び名（エイリアス）で参照するのが慣例となっています．

NumPyは名前が短いのでそのまま書いても良いのですが，“np”という呼び名（エイリアス）で参照するのが慣例なので，それに従っておきます．

もちろん，“as”の後の名称は自分が好きなものを設定して構いません．その場合は，本記事内のソース・コードを適宜読み替えてください．

Matplotlibで表示するグラフの基本的な構造

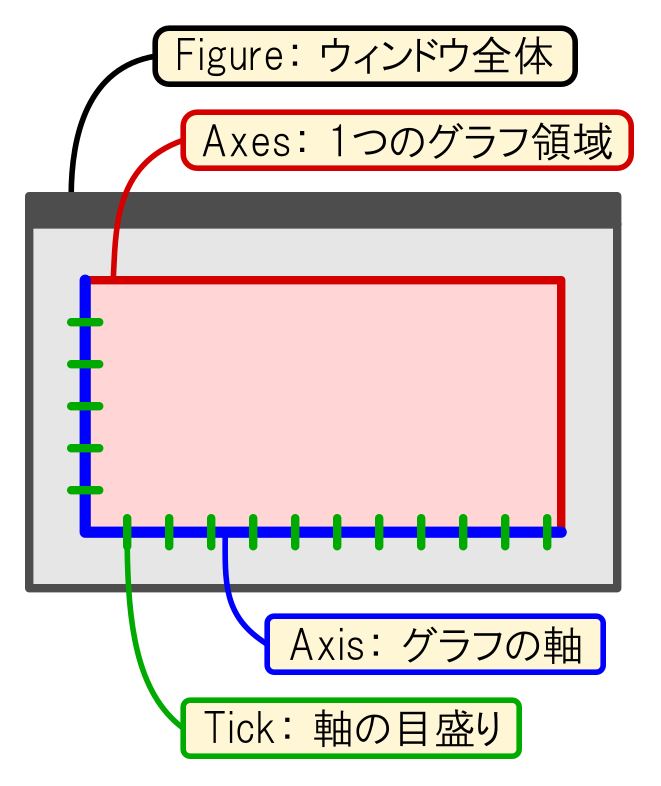
Matplotlibで表示するグラフは，基本的に図2のような構造になっています．各パーツの名前と役割を頭に入れておくと，Matplotlibを利用する上で大いに役立ちます．

図2　Matplotlibのグラフの基本的な構造

Figure

“Figure”（フィギュア）は，Matplotlibで表示するグラフの最上位階層にあたります．グラフを描画する領域全体をFigureとして扱うイメージになります．

本記事ではグラフをウィンドウで表示することを想定していますが，その場合は1つのFigureが1つのウィンドウに対応します．Figureオブジェクトを複数生成すると，複数のウィンドウが表示されます．

Axes

“Axes”（アクシーズ）は，個々のグラフ領域を指します．実際に折れ線グラフや棒グラフ，散布図などを描画するエリアがAxesです．

1つのAxesに複数のグラフを重ねて描くことができます（例えば折れ線グラフと散布図など）．また，1つのFigureの中に複数のAxesを配置することもできます．

Axis

“Axis”（アクシス）は，$x$軸や$y$軸といったグラフの「軸」を指します．2次元プロットなら「$x$軸と$y$軸」，3次元プロットなら「$x$軸と$y$軸と$z$軸」といった具合に，1つのAxesには1セットのAxisが含まれます．

Tick

“Tick”（ティック）は，グラフの軸の「目盛り」を指します．グラフ上に表示するTickの数は設定によって自由に変更できますが，いずれにしても，1つの“Axis”には1セットの“Tick”が含まれています．

“Figure”を1つ作って表示してみる

Figureオブジェクトを作って，グラフの描画領域を表示してみます（リスト2）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()

plt.show()

4行目では，“fig”という名前で新しいFigureオブジェクトを作っています．

6行目の“plt.show()”で，作成したグラフのデータを画面上に表示させています．基本的に“plt.show()”を実行しないかぎり，作成したグラフは画面上に表示されません．

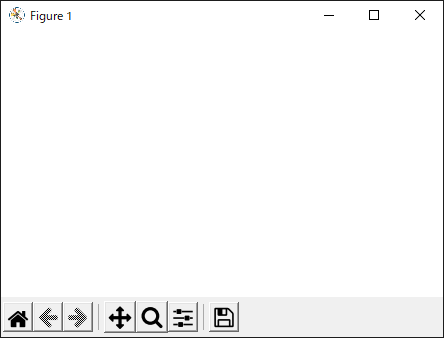
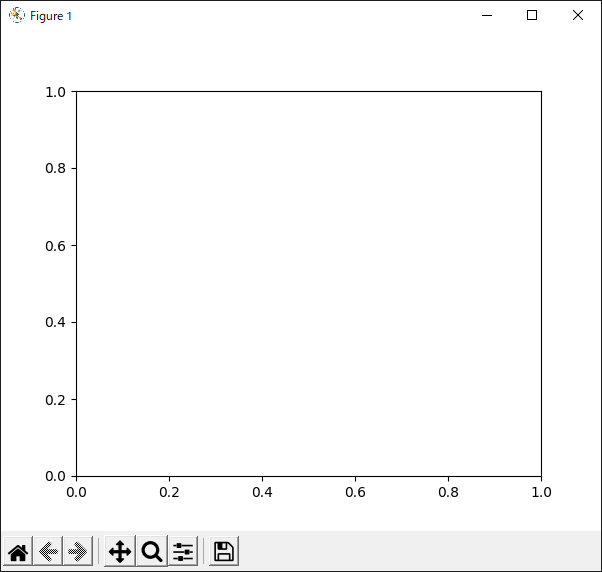
リスト2のプログラムの実行結果を図3に示します．

図3　1つのFigureオブジェクトだけを作って表示させた様子

今回はFigureという「Axes（グラフの描画領域）を入れるための外枠」だけを用意したので，空のウィンドウが表示されます．

“Figure”のサイズを設定する

Figureオブジェクトを作るときに“figsize”というキーワードを使うと，ウィンドウのサイズを設定できます．“figsize=(6, 5)”と書いた場合，“6”は横方向のサイズで“5”は縦方向のサイズとなります．単位は「インチ」です．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )

plt.show()

リスト3 のプログラムの実行結果を図4に示します．

図4　“figsize”キーワードを使ってFigureのサイズを設定した様子

“Figure”の中に1つの“Axes”を作って表示してみる

個々のグラフを扱う単位である“Axes”を1つ作ってみます（リスト4）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

plt.show()

5行目で，“ax1”という名前で新しいAxesオブジェクトを作っています．Axesオブジェクトを作るにはいくつかの方法がありますが，基本的にはFigureクラスが持つ“add_subplot()”メソッドを使います．引数の“1,1,1”は，順に「縦方向のAxesの総数（行数），横方向のAxesの総数（列数），いま作ったAxesの位置を指定する番号（インデックス）」を意味します．“add_subplot()”メソッドの使い方については後で詳しく解説します．

リスト4 のプログラムの実行結果を図5に示します．

図5　Figureオブジェクトの中に空のAxesオブジェクトを1つ作った様子

今回はAxesオブジェクトを作っているので，きちんと「グラフ領域」が表示されています．また，具体的なグラフはプロットしていませんが，きちんと「$x$軸」と「$y$軸」が作られています．つまり，Axisオブジェクトも生成されています．さらに，これらの軸には「目盛り」も付いているので，Axisオブジェクトに含まれるTickオブジェクトも作られていることがわかります．

1つのFigureに複数のAxesを配置する

1つのウィンドウ（Figure）に複数のグラフ（Axes）を並べて表示してみます．

“Figure.add_subplot()”メソッドの使い方

最初に，Figureクラスの“Figure.add_subplot()”メソッドの仕様を確認しておきます．

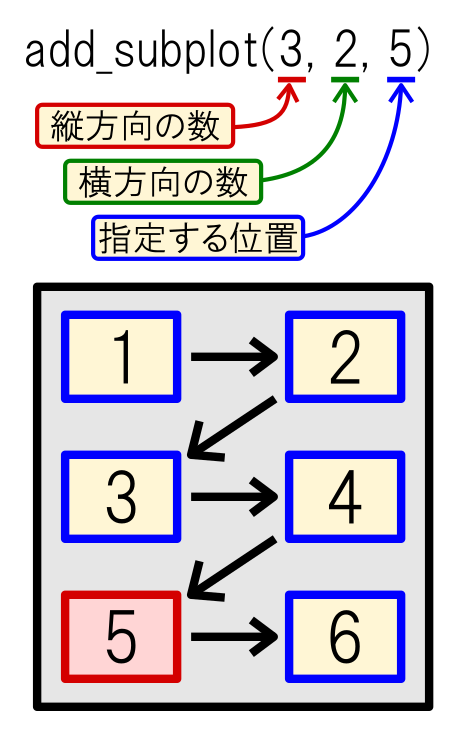
“add_subplot()”メソッドは，Figureに対してAxesを追加するときに使います．例として，“add_subplot(3,2,5)”を実行したときの様子を図6に示します．最初の引数“3”は，Figure全体を縦方向に3分割することを意味します．2番目の引数“2”は，Figure全体を横方向に2分割することを意味します．このとき，Figure全体を$3 \times 2 = 6$個に分割するイメージになります．ここで分割した各領域には，左上から順番に「インデックス」が割り当てられます．最後の引数“5”によって6分割したうちの5番目の領域を指定し，そこにAxesオブジェクトを作成しています．

図6　FigureにAxesを追加する“Figure.add_subplot()”メソッドの使い方

“add_subplot()”メソッドは，新しく作成したAxesオブジェクトを返します．今回は“ax1 = fig.add_subplot(3,2,5)”といった具合に，Axesオブジェクトを格納する変数“ax1”を用意して受けています．

$2\times 2 = 4$個のAxesを並べて表示する

1つのFigureの内部に“$2 \times 2 = 4$”個のAxesを作るプログラムを書いてみます（リスト5）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )

ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
ax4 = fig.add_subplot(2,2,4)

ax1.set_facecolor("skyblue")
ax2.set_facecolor("pink")
ax3.set_facecolor("lightgreen")
ax4.set_facecolor("khaki")

plt.show()

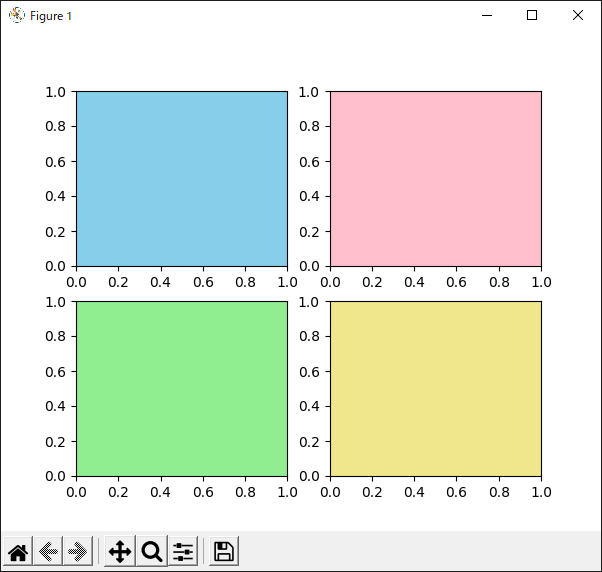
6行目から9行目では“add_subplot()”メソッドを使い，$2 \times 2 = 4$個のAxesを作っています．それらを“ax1”から“ax4”という変数に格納しています．

11行目から14行目では，各Axesの位置を確認するために背景色を設定しています．Axesオブジェクトには“set_facecolor()”というメソッドが用意されており，引数として渡した色（“red”や“blue”など）で塗りつぶすことができます．なお，Matplotlibで使える色の名前は“List of named colors”のページを参照してください．

リスト5のプログラムの実行結果を図7に示します．

図7　$2\times2 = 4$個のAxesを配置した様子

大きさが異なるAxesを並べて表示する

「Figureの左側半分を縦に2分割して2つのAxesを配置し，Figureの右側半分には細長いAxesを1つ配置する」というプログラムを書いてみます（リスト6）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )

ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,3)
ax3 = fig.add_subplot(1,2,2)

ax1.set_facecolor("skyblue")
ax2.set_facecolor("pink")
ax3.set_facecolor("lightgreen")

plt.show()

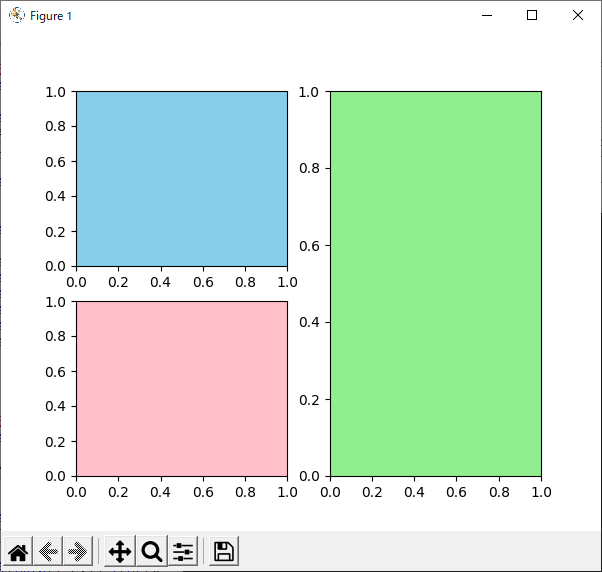
6行目および7行目では，Figure全体を$2 \times 2 = 4$個に分割して，左上の領域（インデックスは“1”）に作成したAxesを“ax1”，左下の領域（インデックスは“3”）に作成したAxesを“ax2”という変数で受けています．

8行目では，あらためてFigure全体を$1 \times 2 = 2$個に分割しています．ここで右側の領域（インデックスは“2”）はまだ使っていないので，ここに作成したAxesを“ax3”という変数で受けています．

また，10行目から12行目では例によって各Axesの見分けが付くように背景色を設定しています．

リスト6 のプログラムを実行した様子を図8に示します．

図8　左側に2つのAxesを並べ，右側に1つのAxesを配置した様子

このように，“add_subplot()”メソッドによる分割は「上書き」することができます．今回は上書きの前後でAxesが干渉していないのでうまくいきましたが，もしAxesが互いに干渉する（複数のAxesが重なる）場合は後から行った操作が優先されます．

簡単なグラフを表示する

“Figure”と“Axes”の基本的な扱い方がわかったので，簡単なグラフを描いてみます（リスト7）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot([1,2,3,4,5], [10, 7, 12, 6, 9])

plt.show()

4行目では“fig”という名前で新しいFigureオブジェクトを作っています．

5行目では“ax1”という名前でAxesオブジェクトを作っています．

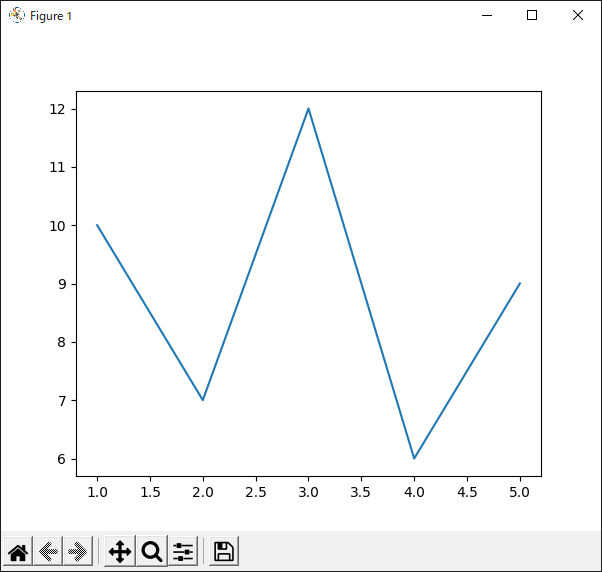
7行目では，Axesオブジェクトが持つ“plot()”メソッドで折れ線グラフを描いています．第1引数の“[1, 2, 3, 4, 5]”は$x$座標のリスト，第2引数の“[10, 7, 12, 6, 9]”は$y$座標のリストです．$x$座標のデータ数と$y$座標のデータ数が異なるとエラーが出るので注意してください．

リスト7のプログラムを実行した様子を図9に示します．

図9　簡単な折れ線グラフを描画した様子

このように“Axes.plot()”メソッドは「折れ線グラフ」を描くときに使いますが，$x$方向のデータ間隔を非常に細かくすれば十分になめらかな「曲線」を描くこともできます．よって，“Axes.plot()”は「一般的な関数（波形）を描くときに使うメソッド」だと言えます．

「明示的」（explicit）な書き方と「暗黙的」（implicit）な書き方

Matplotlibを使うときのソース・コードの書き方には，大きく分けて2つの方法があります．

• 「オブジェクト指向」を意識した「明示的」（explicit）なコーディング
• “MATLAB”に似た使い勝手を実現する「暗黙的」（implicit）なコーディング

ここまで例として示したソース・コードは，すべて「明示的」なコーディングを採用しています．ここでは，もう1つの「暗黙的」なコーディングがどういったものかを簡単に見てみます．

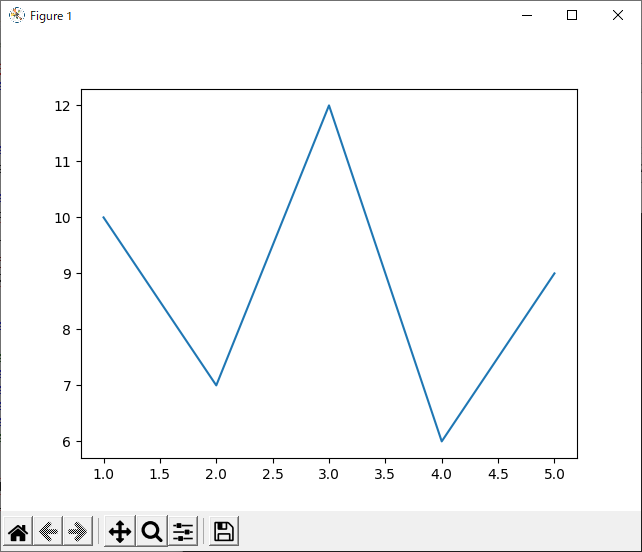
リスト8のソース・コードは，さきほど示したリスト7と同じ処理を「暗黙的」なコーディングで表現したものです．

import matplotlib.pyplot as plt
import numpy as np

plt.plot([1,2,3,4,5], [10, 7, 12, 6, 9])

plt.show()

4行目では，“pyplot”モジュールに含まれる“plot()”関数をいきなり実行してグラフを描いています．この処理の裏ではグラフを描画するための“Figure”や“Axes”が作られているはずですが，ソース・コード上にそれらのオブジェクトが現れることはありません．よって，ユーザはそれらを（表面上は）意識する必要がありません．そのため，このような書き方をMatplotlibの公式ドキュメントでは「暗黙的」な書き方と呼んでいます．

リスト8の実行結果を図10に示します．結果だけ見れば，図9とまったく同じです．

図10　「暗黙的」なコーディングで描画したグラフ

今後は「明示的」な書き方だけを使う

「暗黙的」な書き方は，一見するとコーディング量が減って簡単であるような気がします．実際，MATLABではこれが標準的なインターフェースとして採用されているようです．

ところが，「暗黙的」な書き方をしてしまうと我々がグラフを作る際に操作するFigureやAxesといったオブジェクトが見えないので，サイズの変更や色の設定といった細かい操作がやりづらくなってしまいます．こういった問題は，描きたいグラフが複雑になるほど顕著になります．Matplotlibの公式ドキュメントには「明示的なコーディングの方が細かい設定が可能であり柔軟性にも富む」と書かれており，オブジェクト指向に沿った「明示的」なコーディングを推奨しているようです．

以上のことから，今後は常に「明示的」なコーディングに統一してソース・コードを書くことにします．ただし，Web上で公開されている様々なサンプル・コードには「暗黙的」な書き方も多く含まれており，それらは決して間違っているわけではありません．

グラフを描く時によく使う“NumPy”のノウハウ

数値計算用ライブラリである“NumPy”には，非常に多くの機能が含まれています．ここでは，グラフを描くときによく使うNumPyの基本的なノウハウを紹介します．

NumPy配列を作る“numpy.array()”

Pythonには「リスト」や「タプル」といった，いわゆる配列タイプのデータ型が用意されています．これに対して，NumPyには数値計算における効率を改善した“ndarray”（N-dimensional array，「多次元配列」の略）という型が用意されています．ndarray型のNumPy配列を作るには，リスト9のように“numpy.array()”関数を使います．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3, 4, 5] )
print(a)
print( type(a) )

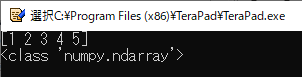
4行目では，“numpy.array()”メソッドを使ってPythonのリストから“ndarray”型のNumPy配列を作っています．

5行目では作成したNumPy配列をそのまま表示しています．

6行目では“type()”関数を使ってNumPy配列の型を確認しています．

リスト9のプログラムの実行結果を図11に示します．

図11　“ndarray”型のNumPy配列を作った様子

“ndarray”型のNumPy配列には，普通のPythonのリストには無い様々な機能があります．また，Matplotlibの内部では配列を“ndarray”型に変換した上で実行されているそうです．よって，今後は基本的に“ndarray”型のNumPy配列だけを扱うものとします．

NumPy配列におけるスライス

Pythonのリストと同様に，NumPy配列にも要素の一部をまとめて取り出す「スライス」という仕組みがあります．

基本的な書式は，配列のインデックスを指定する“[ ]”の中に“[start:stop:step]”という形で記述します．最初の“start”は抽出する部分の始点のインデックスです．真ん中の“stop”は終点のインデックスです．このとき指定される最後の要素のインデックスは“stop-1”となります（インデックスが“stop”の要素は含まれない）．最後の“step”は抽出する要素の間隔を指定します．抽出する際に「抜かされる要素の個数」は“step - 1”個となります．

簡単な例で実験してみます（リスト10）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3, 4, 5, 6, 7, 8, 9] )

print( a[0:5], end="\n\n" )
print( a[:5], end="\n\n")
print( a[3:], end="\n\n")
print( a[::2] )

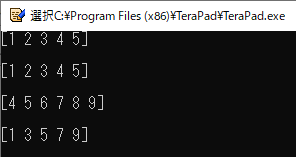
4行目では，1から9までの数値を要素としてもつNumPy配列“a”を定義しています．

6行目では“a[0:5]”としてインデックスが“0”（1番目の要素）からインデックスが“4”（5番目の要素）までを抽出しています．

7行目の“a[:5]”のように始点のインデックスを省略すると，配列の最初（つまりインデックス“0”）が始点になります．

8行目の“a[3:]”のように終点のインデックスを省略すると，配列の最後（つまりインデックス“-1”）が終点になります．

9行目では“a[::2]”として，配列の最初から最後までの要素を対象として，1個おきに要素を抽出しています．

リスト10の実行結果を図12に示します．

図12　「スライス」を使ってNumPy配列の一部を抽出した結果

2次元配列でスライスを使う

「スライス」は2次元配列に対しても使えます（リスト11）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [ [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16] ] )

print( a, end="\n\n" )
print( a[2][1], end="\n\n" )
print( a[2, 1], end="\n\n" )

print("=================================")

print( a[0:2, 2:4], end="\n\n" )
print( a[:, 0], end="\n\n" )
print( a[1, :] )

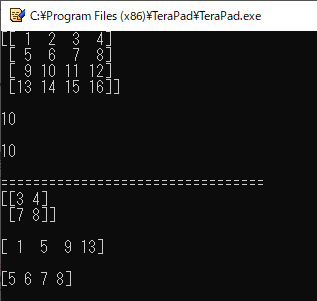
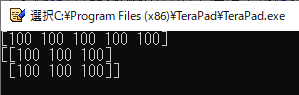
4行目では，“a”という名前で2次元のNumPy配列（行列）を定義しています．

6行目では，NumPy配列“a”をそのまま表示しています．なお，printした結果を見やすくするために，末尾に改行文字を2個付けています．

7行目では，配列の中の1つの要素にアクセスしています．普通のPythonの2次元リストは“list[行][列]”という形で要素にアクセスしますが，これはNumPy配列でも同様です．“a[2][1]”として「3行，2列」の要素つまり“10”という値を取り出しています．

なお，行列として表記した場合「3行目」はタテ方向に3番目の要素，「2列目」はヨコ方向に2番目の要素という意味です．ややこしいですが，タテ方向に「1行目」，「2行目」，...と数えることから，「行」とは「ヨコ方向に並んだ数のまとまり」を指すことになります．また，横方向に「1列目」，「2列目」，...と数えることから，「列」とは「タテ方向に並んだ数のまとまり」を指します．

8行目では，7行目と同じく「3行，2列」の要素にアクセスしています．ただし，NumPy配列ではこれを“a[2,1]”のようにカンマで区切って表記することができます．

12行目では，2次元配列に対して「スライス」を使っています．“a[0:2, 2:4]”と書くことで「行方向のインデックスが“0”から“1”」，「列方向のインデックスが“2”から“3”」の領域を取り出しています．

13行目のように“a[:, 0]”と書くと「行方向は全て」，「列方向のインデックスは0」の要素を取り出せます．

14行目のように“a[1, :]”と書くと「行方向のインデックスは1」，「列方向は全て」の要素を取り出せます．

リスト11の実行結果を図13に示します．

図13　2次元のNumPy配列に対して「スライス」を使った結果

NumPy配列どうしの演算

NumPy配列どうしの演算をやってみます（リスト12）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3, 4, 5] )
b = np.array( [10, 20, 30, 40, 50] )
c = a + b

print(c)

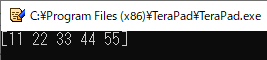
4行目および5行目では，NumPy配列として変数“a”および“b”を定義しています．

6行目では，“a”と“b”の和を変数“c”に格納しています．

リスト12の実行結果を図14に示します．

図14　NumPy配列どうしの「たし算」の結果

図14の結果を見ると，「同じ位置の要素どうしのたし算」が実行されていることがわかります．

もう1つの例を見てみます．今度は「かけ算」です（リスト13）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3, 4, 5] )
b = np.array( [10, 20, 30, 40, 50] )
c = a * b

print(c)

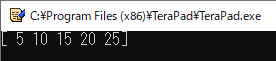
4行目と5行目では，さきほどと同じ値で配列“a”と“b”を定義しています．

6行目では“a”と“b”の「かけ算」を実行し，その結果を変数“c”に格納しています．

リスト13の実行結果を図15に示します．

図15　NumPy配列どうしの「かけ算」の結果

やはり，「同じ位置の要素どうしのかけ算」が実行されていることが確認できました．

今回はNumPy配列が1次元（ベクトル）の場合について確認しましたが，2次元（行列）やそれ以上のネスト構造の場合も同様に計算されます．

NumPy配列の演算における「ブロードキャスト」

NumPy配列には，「ブロードキャスト」と呼ばれる非常に強力な仕組みがあります．簡単な例で見てみましょう（リスト14）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3, 4, 5] )
b = 5
c = a * b

print(c)

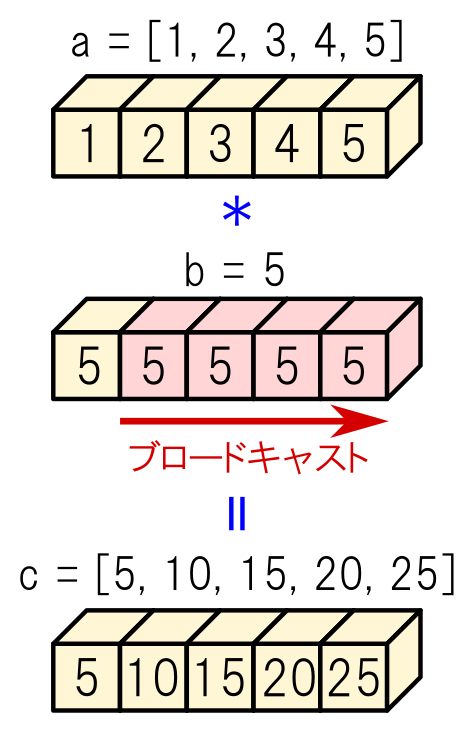
4行目では，NumPy型の配列として変数“a”を定義しています．

5行目では，普通の数（スカラ）として変数“b”を定義しています．

6行目では“a*b”という「かけ算」を実行して，その結果を変数“c”に格納しています．

もしPythonの普通のリストでこのような計算を実行すると，“[1,2,3,4,5]”が5回繰り返されるような配列が得られます．これに対して，NumPy配列の場合は図16に示すように「変数“a”の各要素が“b”倍される」という結果が得られます．

図16　NumPy配列（ベクトル）と定数（スカラ）のかけ算において「ブロードキャスト」がはたらいていることがわかる

これがNumPy配列における「ブロードキャスト」です．「ブロードキャスト」の様子は，図17のようなイメージで理解できます．

変数“b”はもともと単一の数（要素が1つの配列とも言える）ですが，“a*b”という演算を実行すると自動的に“b”のサイズがNumPy配列“a”のサイズと等しくなるように調整されています．

図17　NumPy配列の演算における「ブロードキャスト」のイメージ

Numpyには“numpy.sin()”や“numpy.log()”のように，“sin()”や“log()”の値を計算する関数が用意されています．これらの関数にNumPy配列を渡した場合も「ブロードキャスト」が有効になります（リスト15）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3, 4, 5] )
b = np.sin( a )

print(b)

4行目では，“[1, 2, 3, 4, 5]”というNumPy配列“a”を用意しています．

5行目では“numpy.sin()”の引数にNumPy配列“a”を渡し，その計算結果を変数“b”に格納しています．

リスト15のプログラムの実行結果を図18に示します．

図18　“numpy.sin()”の計算でも「ブロードキャスト」がはたらいている

“sin(a)”は，NumPy配列“a”の各要素に対して“sin()”を実行した結果をまとめた配列になっています．

なお，NumPy公式ドキュメントでは“broadcasting”（ブロードキャスティング）という表記になっていますが，本記事では一貫して「ブロードキャスト」と呼ぶことにします．

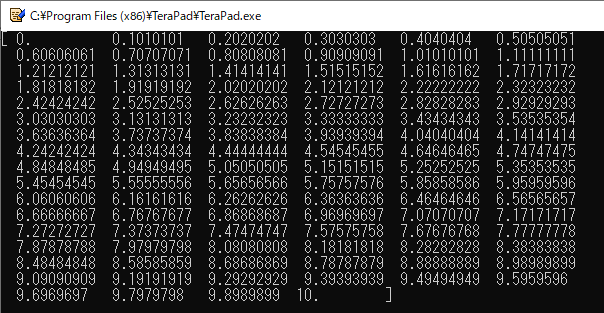
“numpy.linspace()”で「始点」，「終点」，「要素数」を指定して配列を作る

グラフを描くときに，独立変数（基本的には$x$軸側のデータ）として適当な等差数列を作りたくなることがあります．そういったときは，“numpy.linspace()”関数を使うと便利です（リスト16）．“linspace”は“linear spaced vector”の略であり，「線形の間隔を持つベクトル」すなわち「要素の番号に比例して値が増加する配列」を作る関数です．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 10, 100)

print(x)

4行目で“numpy.linspace()”関数を使って等差数列を作り，変数“x”に格納しています．この“x”はNumPy配列となります．

“numpy.linspace()”の第1引数は「始点」，第2引数は「終点」，第3引数は作る配列の要素数（分割数）です．出力される配列には「始点」と「終点」の両方の値が含まれます．

リスト16の実行結果を図19に示します．

図19　“numpy.linspace()”で等差数列を作った様子

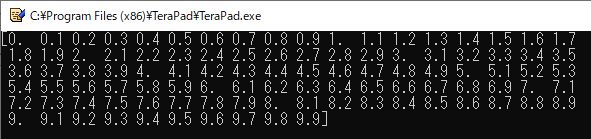
“numpy.arange()”で「始点」，「終点」，「間隔」を指定して配列を作る

“numpy.arange()”は先ほどの“numpy.linspace()”と同じく等差数列を作る関数ですが，挙動が少し異なります（リスト17）．

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 10, 0.1)

print(x)

4行目で“numpy.arange()”関数を使い，等差数列を作っています．第1引数は「始点」，第2引数は「終点」，第3引数は間隔を指定します．ただし，デフォルトでは「終点」の値は含まれません．

リスト17の実行結果を図20に示します．

図20　“numpy.arange()”で等差数列を作った様子

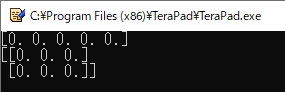
“numpy.zeros()”で“0”だけの配列を作る

“numpy.zeros()”を使うと，値として“0”だけを持つ配列を作れます（リスト18）．

import matplotlib.pyplot as plt
import numpy as np

z1 = np.zeros(5)
z2 = np.zeros( (2,3) )

print(z1)
print(z2)

4行目では，5個の要素を持つ配列（ベクトル）を作っています．“numpy.zeros()”の引数は，作成するNumPy配列のサイズを渡します．

5行目では，1行あたり3個の要素を持つ2次元配列（$2\times3$行列）を作っています．

リスト18のプログラムの実行結果を図21に示します．

図21　“numpy.zeros()”で“0”だけの配列を作った様子

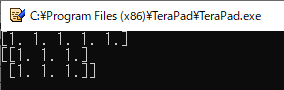
“numpy.ones()”で“1”だけの配列を作る

“numpy.ones()”を使うと，値として“1”だけを持つ配列を作れます（リスト19）．

import matplotlib.pyplot as plt
import numpy as np

one1 = np.ones(5)
one2 = np.ones( (2,3) )

print(one1)
print(one2)

4行目では，5個の要素を持つ配列（ベクトル）を作っています．“numpy.ones()”の引数は，作成するNumPy配列のサイズを渡します．

5行目では，1行あたり3個の要素を持つ2次元配列（$2\times3$行列）を作っています．

リスト19を実行した様子を図22に示します．

図22　“numpy.ones()”で“1”だけの配列を作った様子

“numpy.full()”で任意の定数だけの配列を作る

“numpy.full()”を使うと，任意の値だけを持つ配列を作れます（リスト20）．

import matplotlib.pyplot as plt
import numpy as np

f1 = np.full(5, 100)
f2 = np.full( (2,3), 100 )

print(f1)
print(f2)

4行目では，5個の要素を持つ配列（ベクトル）を作っています．“numpy.full()”の第1引数は，作成するNumPy配列のサイズを渡します．また，第2引数は要素の値を指定します．今回は“100”としました．

5行目では，1行あたり3個の要素を持つ2次元配列（$2\times3$行列）を作っています．

図23　“numpy.full()”を使ってすべての要素が“100”の配列を作った様子

“numpy.dot()”でベクトルの「内積」を計算する

2つのベクトルの「内積」を計算する時は，“numpy.dot()”関数を使います．例えば，要素が3個の配列（3次元ベクトル）どうしの「内積」は次のように定義されています．

また，この関数の引数に2次元配列（行列）を渡すと，いわゆる「行列どうしの積」が得られます．要素が$2\times 2$個の配列（$2\times 2$行列）どうしの「積」は次のように定義されています．

なお，NumPy配列として定義された行列どうしの積は“@”でも計算できます（リスト21）．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3] )
b = np.array( [4, 5, 6] )
c = np.dot(a, b)
print(c, end="\n\n")

d = np.array( [ [1, 2], [3, 4] ] )
e = np.array( [ [1, 1], [0, 1] ] )
f = np.dot(d, e)
print(f, end="\n\n")

g = d @ e
print(g)

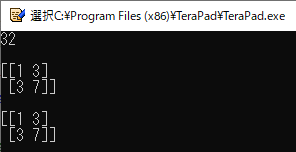
4行目と5行目では，1次元配列（ベクトル）として変数“a”および“b”を定義しています．

6行目で“numpy.dot()”関数を使い，これらの「内積」を計算して変数“c”に格納しています．

7行目では，この計算結果をprintしています．

9行目と10行目では，$2 \times 2$行列を定義しています．

11行目で“numpy.dot()”関数を使い，これらの行列の「積」を計算しています．

14行目では「行列どうしの積」を“@”記号を使って実行しています．

リスト21のプログラムの実行結果を図24に示します．

図24　“numpy.dot()”関数を使ってベクトルの「内積」および行列の「積」を計算した様子

“numpy.cross()”でベクトルの「外積」を計算する

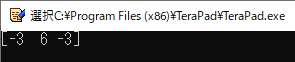
2つのベクトルの「外積」を計算する時は，“numpy.cross()”関数を使います（リスト22）．なお，3次元ベクトルどうしの「外積」は次のように定義されています．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3] )
b = np.array( [4, 5, 6] )
c = np.cross(a, b)

print(c)

リスト22 の実行結果を図25に示します．

図25　“numpy.cross()”を使ってベクトルの「外積」を計算した様子

“numpy.outer()”でベクトルの「直積」を計算する

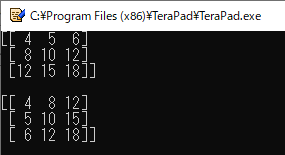
“numpy.outer()”関数を使うと，2つのベクトルの「直積」（ちょくせき）を計算できます（リスト23）．3次元ベクトルどうしの直積は，次のように定義されています．

直積は「内積」や「外積」と比べると使用頻度が少ないですが，覚えておくと3次元プロット用のメッシュを計算する時などに活用できます．

import matplotlib.pyplot as plt
import numpy as np

a = np.array( [1, 2, 3] )
b = np.array( [4, 5, 6] )

c = np.outer(a, b)
print(c, end="\n\n")

d = np.outer(b, a)
print(d)

7行目では直積“$a \otimes b$”を計算して，8行目でその結果を表示しています．

10行目では直積の順序を入れ替えて“$b \otimes a$”を計算し，11行目でその結果を表示しています．

リスト23のプログラムの実行結果を図26に示します．

図26　“numpy.outer()”を使ってベクトルの「直積」を計算した様子

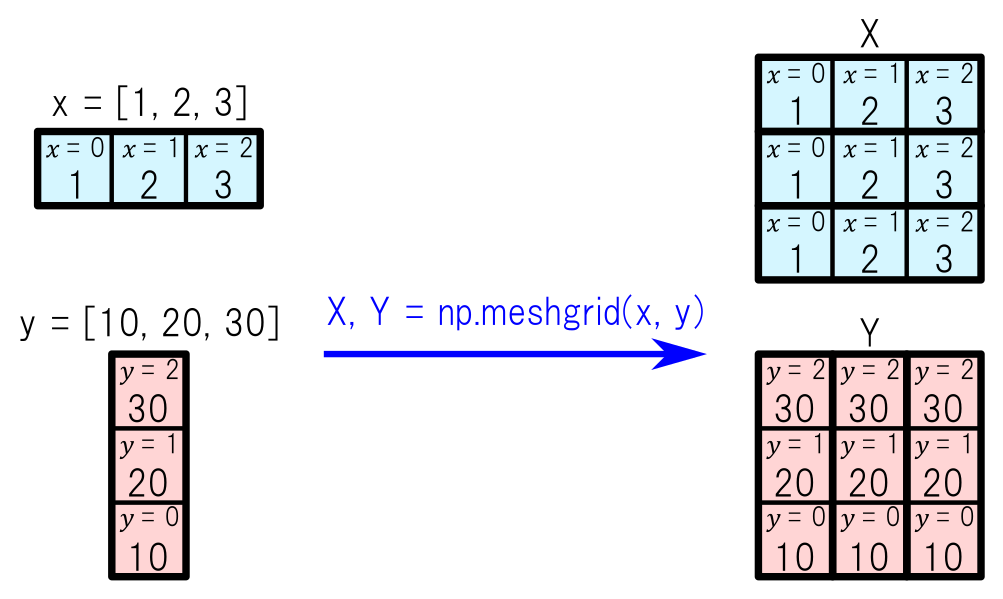
“numpy.meshgrid()”でメッシュを作成する

2次元や3次元の「場」（スカラ場やベクトル場）をプロットするときは，その土台となる「メッシュ」が必要になります．“numpy.meshgrid()”関数を使うと，メッシュを簡単に作ることができます．

“numpy.meshgrid()”で2次元のメッシュを作るときのイメージを図27に示します．

図27　“numpy.meshgrid()”関数で2次元のメッシュを作るイメージ

ここでは例として，$x$方向のメッシュの座標を“[1, 2, 3]”とします．また，$y$方向のメッシュの座標を“[10, 20, 30]”とします．

$x$座標用のメッシュ（上図の“X”）を作るためには，$x$方向の座標“[1, 2, 3]”を$y$方向の要素の数だけ繰り返し並べる必要があります．また，$y$座標用のメッシュ（上図の“Y”）は，$x$側が最初に“[1, 2, 3]”と変化する間は“10”という一定値を保ち，$x$側が2回目に“[1, 2, 3]”と変化する間は“20”という一定値を保ち...といった具合に，$x$方向の要素の数だけ$y$方向の値を繰り返す必要があります．

“numpy.meshgrid()”は，引数の配列“x”および“y”をもとにして，メッシュ用の$x$座標をまとめた2次元配列“X”とメッシュ用の$y$座標をまとめた2次元配列“Y”を作成して返してくれます（リスト24）．

import matplotlib.pyplot as plt
import numpy as np

x = np.array( [1, 2, 3] )
y = np.array( [10, 20, 30] )

X, Y = np.meshgrid(x, y)

print(X, end="\n\n")
print(Y)

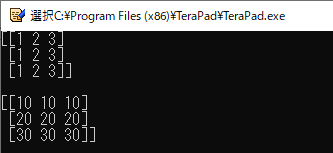
4行目と5行目では，メッシュのもとになる$x$座標の配列と$y$座標の配列を作っています．

7行目で，“numpy.meshgrid()”関数を使って配列“x”および“y”からメッシュを作っています．“numpy.meshgrid()”の返り値は，$x$座標用のメッシュと$y$座標用のメッシュの2つです（これは2つの配列を引数に渡した場合で，3つの配列を渡せば3つの返り値が得られる）．この2つの返り値を“X”および“Y”という変数名で受け取っています．

9行目では$x$座標用のメッシュ“X”を表示して確認しています．

10行目では$y$座標用のメッシュ“Y”を表示しています．

リスト24のプログラムの実行結果を図28に示します．

図28　“numpy.meshgrid()”を使って2次元のメッシュを作った様子

なお，同様の手順で3次元のメッシュを作ることもできます．

グラフの体裁を整える

グラフの線の太さや色，座標軸の大きさやラベルなど，見栄えを細かく設定する方法を紹介します．

もとになるグラフを描く

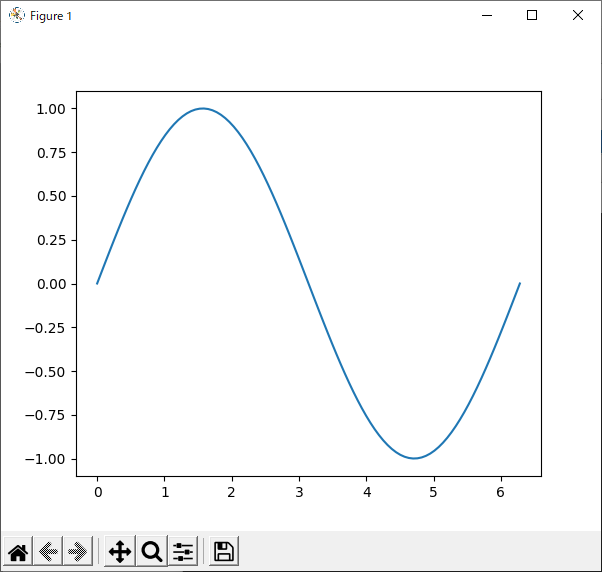
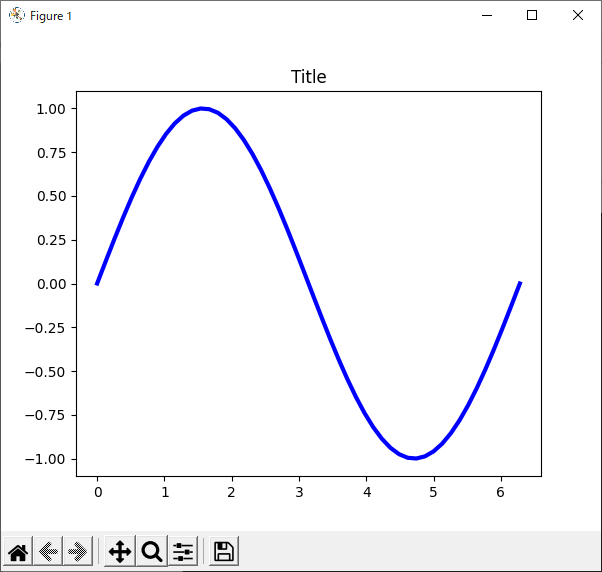
まずは，見栄えを調整する前の「sin関数を描いただけのグラフ」を用意します（リスト25）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y)

plt.show()

4行目では$0$から$2\pi$までの間を100分割した配列“x”を作っています．

5行目では$\sin(x)$の値を計算して，配列“y”に格納しています．

7行目，8行目ではグラフ描画領域を作成しています．

10行目でsin関数を描画し，12行目でグラフを表示させています．

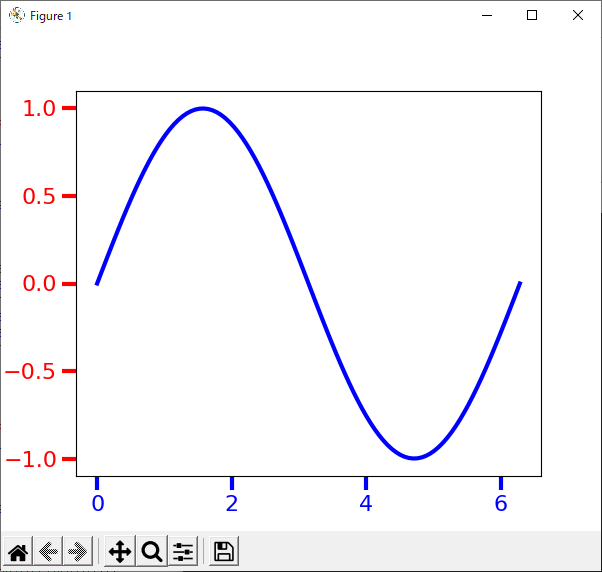
リスト25のプログラムの実行結果を図29に示します．

図29　sin関数のグラフを描いた様子

これから，このグラフの見栄えを調整していきます．

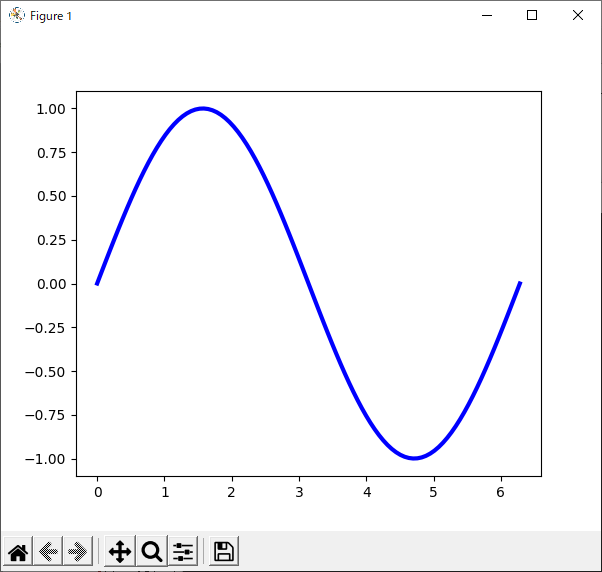
“color”キーワードで線の色を設定する

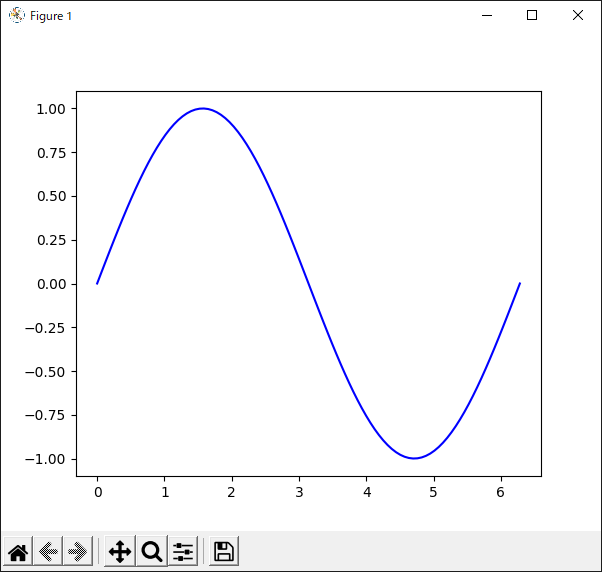
“Axes.plot()”メソッドで描画した線の色を変えるには，“color”キーワードを使います（リスト26）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue")

plt.show()

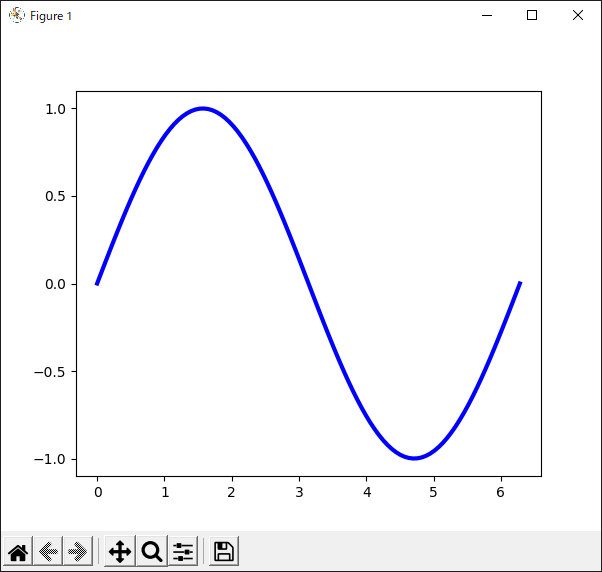
10行目の“plot()”メソッドの引数として“color”キーワードを使い，色を“blue”に指定しています．“color”を省略して“c”と表記することもできます．Matplotlibで使える色の名前は“List of named colors”のページを参照してください．

リスト26のプログラムの実行結果を図30に示します．

図30　グラフの線色を青にした様子

“linewidth”キーワードで線の幅を設定する

“Axes.plot()”メソッドで描画した線の幅を変えるには，“linewidth”キーワードを使います（リスト27）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", linewidth=3)

plt.show()

10行目の“plot()”メソッドの引数として“linewidth”キーワードを使い，線幅を“3”に設定しています．値が大きいほど太い線幅で描画されます．なお，“linewidth”を略して“lw”と書くこともできます．

リスト27のプログラムの実行結果を図31に示します．

図31　グラフの線幅を“3”にした様子

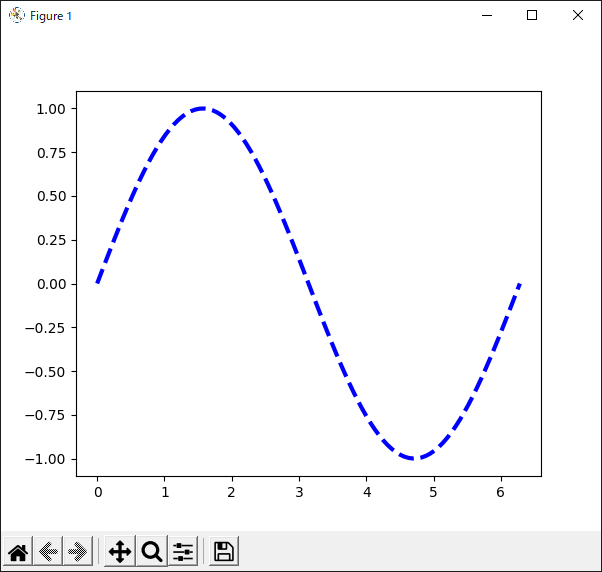
“linestyle”キーワードで線の種類を設定する

“Axes.plot()”メソッドで描画した線のスタイルを変更するには，“linestyle”キーワードを使います（リスト28）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", linewidth=3, linestyle="--")

plt.show()

10行目の“plot()”メソッドの引数として“linestyle”キーワードを使い，破線で表示しています．他には“:”（点線）や“-.”（鎖線）などを指定できます．“linestyle”を省略して“ls”と書くこともできます．

リスト28のプログラムの実行結果を図32に示します．

図32　グラフの線種を破線にした様子

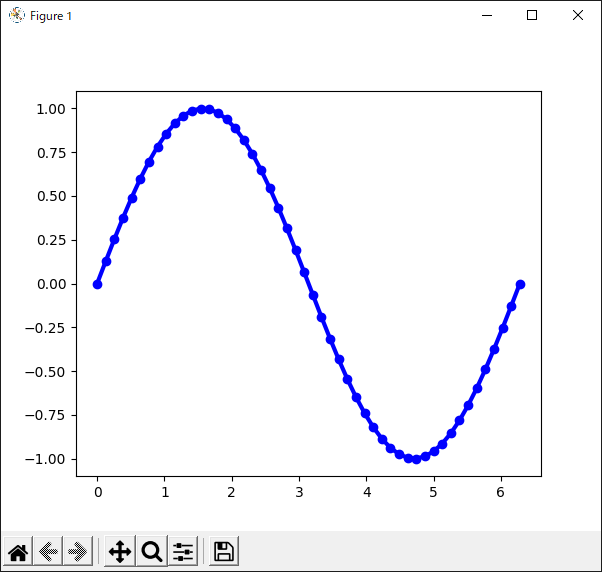
“marker”キーワードでマーカーを設定する

“Axes.plot()”メソッドで描画したグラフにマーカーを追加するには，“marker”キーワードを使います（リスト29）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 50)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3, marker="o")

plt.show()

10行目の“plot()”メソッドの引数として“marker”キーワードを使い，マーカーの設定をしています．今回は“o”として丸いマーカーを設定しました．他には“s”（四角形），“x”（細いバツ），“X”（太いバツ），“D”（ダイアモンド形），“*”（星形）などを指定できます．

リスト29のプログラムの実行結果を図33に示します．

図33　グラフに丸いマーカーを追加した様子

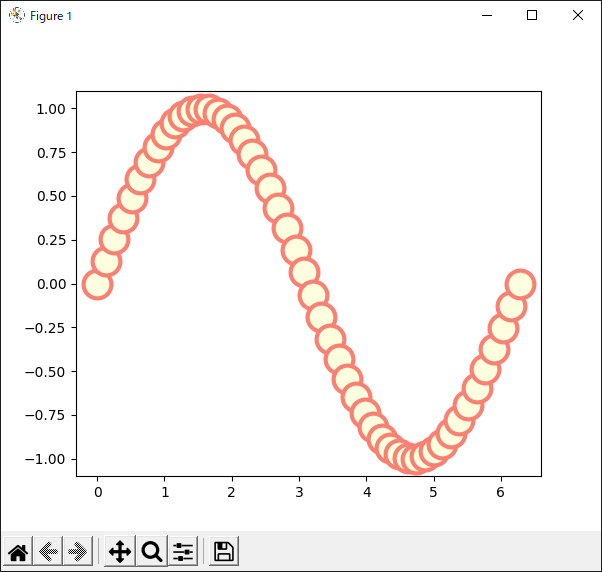
“ms”，“mec”，“mew”，“mfc”キーワードでマーカーの色などを設定する

マーカーの大きさや色，輪郭などを設定してみます（リスト30）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 50)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3, marker="o", ms=20, mec="salmon", mew=3, mfc="lightyellow")

plt.show()

10行目の“plot()”メソッドの引数として，マーカーの見栄えを設定するキーワードをいくつか使っています．

マーカーのサイズを設定するには“markersize”あるいは“ms”というキーワードを使います．今回は“ms = 20”としています．

マーカーの輪郭の色を設定するには“markeredgecolor”あるいは“mec”というキーワードを使います．今回は“salmon”（サーモン）という色にしてみました．

マーカーの輪郭の線幅を設定するには“markeredgewidth”あるいは“mew”というキーワードを使います．今回は“mew = 3”としています．

マーカー内部の色を設定するには“markerfacecolor”あるいは“mfc”というキーワードを使います．今回は“lightyellow”（ライト イエロー）という色に設定しました．

リスト30のプログラムの実行結果を図34に示します．

図34　マーカーの色や大きさを設定した様子

“Axes.set_title()”メソッドでグラフのタイトルを設定する

グラフ領域（Axesオブジェクト）の上にタイトルを表示するには，“Axes.set_title()”メソッドを使います（リスト31）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.set_title("Title")

plt.show()

12行目で“set_title()”メソッドを使い，“Title”という文字列をタイトルに設定しています．

リスト31のプログラムの実行結果を図35に示します．

図35　グラフの上に“Title”という文字が表示された

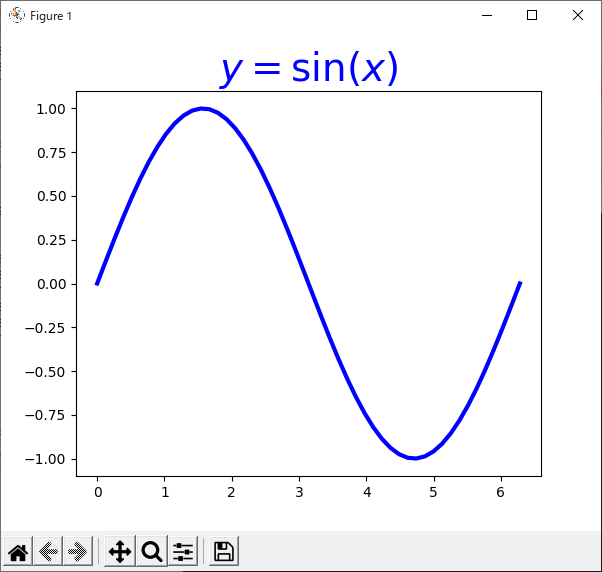
タイトルの文字色や大きさを変えるには，“set_title()”メソッドで“color”や“fontsize”といったキーワードを使います．使用例をリスト32に示します．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.set_title(r"$y = \sin(x)$", color="blue", fontsize=28)

plt.show()

12行目でタイトルの色やフォント・サイズを設定しています．

Matplotlibでは，文字列にTeX（テフ）の記法を使うことができます．いわゆるインライン数式モードの感覚で，“$”記号で囲んだ部分がTeXの文法で解釈されます．なお，TeX表記を使う場合は文字列の前に“r”を付けて「raw文字列」として記述することをおすすめします（TeXでよく使う“\”記号をそのまま文字として認識させたいから）．

リスト32のプログラムの実行結果を図36に示します．

図36　タイトルのサイズや文字色を設定した様子

“Axes.set_xlabel()”，“Axes.set_ylabel()”メソッドで軸のラベルを設定する

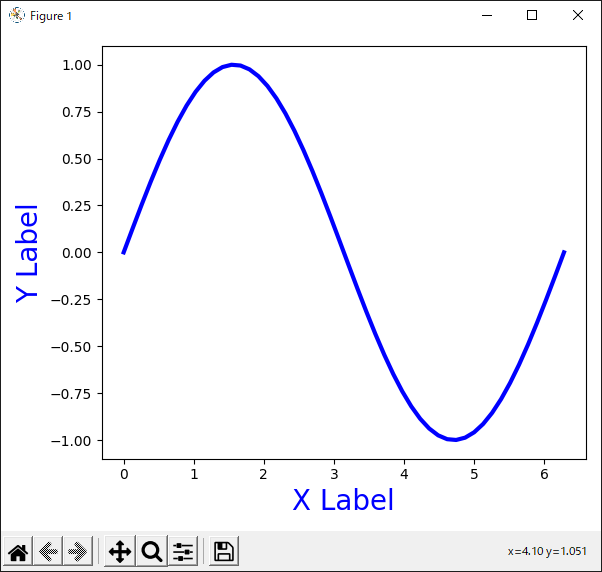
$x$軸や$y$軸のラベルを設定するには“Axes.set_xlabel()”および“Axes.set_ylabel()”メソッドを使います（リスト33）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.set_xlabel("X Label", fontsize=20, color="blue")
ax1.set_ylabel("Y Label", fontsize=20, color="blue")

fig.tight_layout()

plt.show()

12行目で“set_xlabel()”メソッドを使い，$x$軸のラベルを設定しています．同様に，13行目で$y$軸のラベルを設定しています．

リスト33のプログラムの実行結果を図37に示します．

図37　$x$軸と$y$軸のラベルを設定した様子

“Axes.set_xlim()”，“Axes.set_ylim()”メソッドで軸の範囲を設定する

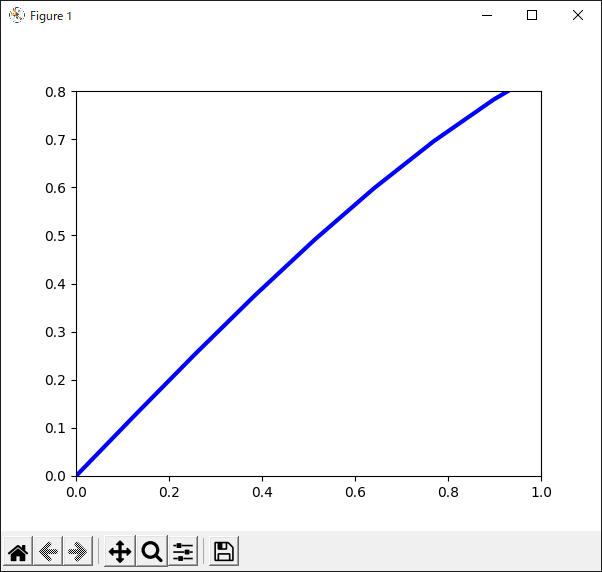
軸の値の範囲を設定するには，“Axes,set_xlim()”および“Axes.set_ylim()”メソッドを使います（リスト34）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.set_xlim(0, 1)
ax1.set_ylim(0, 0.8)

plt.show()

12行目で$x$軸の範囲を“$0\leq x \leq 1$”に，13行目で$y$軸の表示範囲を“$0 \leq y \leq 0.8$”に設定しています．

リスト34のプログラムの実行結果を図38に示します．

図38　$x$軸と$y$軸の表示範囲を設定した様子

“Axes.tick_params()”メソッドで目盛りの色や大きさを設定する

軸の目盛りの見栄えを調整するには“Axes.tick_params()”メソッドを使います（リスト35）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.tick_params(axis="x", length=10, width=3, color="blue", colors="blue", labelsize=16)
ax1.tick_params(axis="y", length=10, width=3, color="red", colors="red", labelsize=16)

plt.show()

12行目の“tick_params()”メソッドでは，第1引数を“axis=x”として設定対象を$x$軸にしています．“length”キーワードは目盛りの長さ，“width”キーワードは目盛りの太さを設定するために使います．“color”キーワードは目盛り線の色で，“colors”キーワードは目盛りのラベル（今回の場合は0,2,4,6という数字）の色に対応しています．“labelsize”キーワードで目盛りのフォント・サイズを設定します．

13行目では“axis=y”として，$y$軸の目盛りに関する設定を行っています．

リスト35のプログラムの実行結果を図39に示します．

図39　軸の目盛りの色や大きさを設定した様子

“Axes.set_xticks()”，“Axes.set_yticks()”メソッドで目盛りの値を設定する

軸の目盛りの値を設定するには“Axes.set_xticks()”，“Axes.set_yticks()”メソッドを使います（リスト36）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

x_ticks = np.arange(0, 2*np.pi, 1)
y_ticks = np.linspace(-1, 1, 5)

ax1.set_xticks(x_ticks)
ax1.set_yticks(y_ticks)

plt.show()

12行目で$x$軸の目盛りとして使う配列を定義しています．今回は“0”から“$2\pi$”まで，“1”間隔としました．

13行目では$y$軸の目盛りとして使う配列を定義しています．今回は“-1”から“1”までの間を“5”等分する形にしました．

15行目で$x$軸の目盛りを設定しています．また，16行目では$y$軸の目盛りを設定しています．

リスト36のプログラムの実行結果を図40に示します．

図40　目盛りの値を設定した様子

なお，軸に目盛りを表示しない場合は次のように“set_xticks( [ ] )”，“set_yticks( [ ] )”と記述します（リスト37）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.set_xticks([])
ax1.set_yticks([])

plt.show()

リスト37のプログラムの実行結果を図41に示します．

図41　軸の目盛りを消した様子

“Axes.grid()”メソッドでグリッドを表示する

グラフにグリッドを表示するときは，“Axes.grid()”メソッドを使います（リスト38）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y, color="blue", lw=3)

ax1.grid()

plt.show()

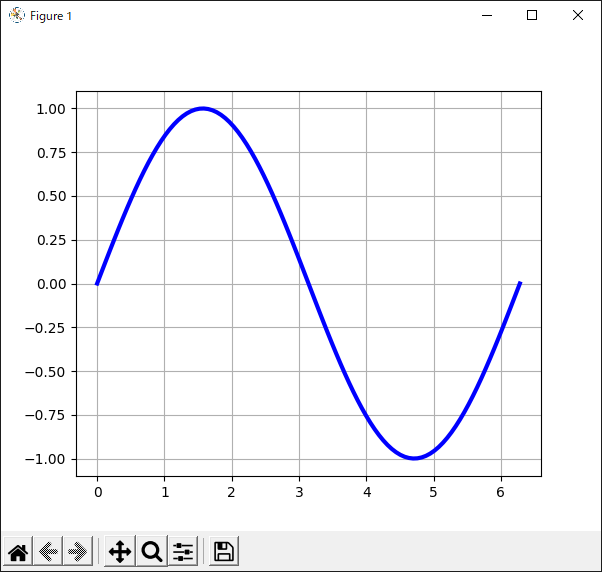
12行目で“grid()”メソッドを呼んでグリッドを表示させています．引数に“linewidth”や“linestyle”などのキーワードを使えば線の太さや種類を設定できます．

リスト38のプログラムの実行結果を図42に示します．

図42　グリッドを表示した様子

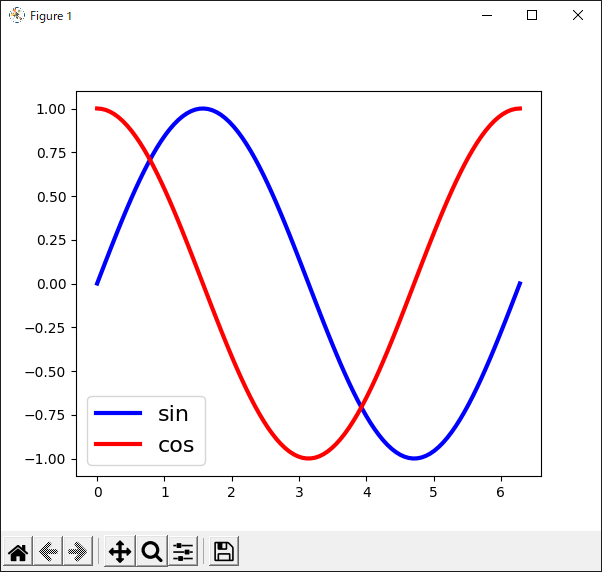
“Axes.legend()”メソッドで凡例を表示する

グラフに凡例を表示するときは“Axes.legend()”メソッドを使います（リスト39）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2*np.pi, 100)
y1 = np.sin(x)
y2 = np.cos(x)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.plot(x, y1, color="blue", lw=3, label="sin")
ax1.plot(x, y2, color="red", lw=3, label="cos")

ax1.legend( fontsize=16 )

plt.show()

5行目では1周期分のsin関数の値を“y1”に，6行目では1周期分のcos関数の値を“y2”に格納しています．

11行目で“y1”のグラフをプロットしています．このとき“label”キーワードを使って凡例として表示する文字列を設定します．今回は“sin”という文字列を設定しました．

12行目でも同じく，“y2”のグラフをプロットする時に“label”キーワードで凡例を設定します．こちらは“cos”という文字列にしました．

14行目のように“legend()”メソッドを呼ぶと，グラフ中に凡例が表示されます．今回は“fontsize”キーワードを使って文字の大きさを設定しました．

リスト39のプログラムの実行結果を図43に示します．

図43　凡例を表示した様子

その他の項目

“pyplot.plot()”関数には，他にも多くの設定項目があります．詳細はAPIリファレンスを参照してください．

散布図を描く

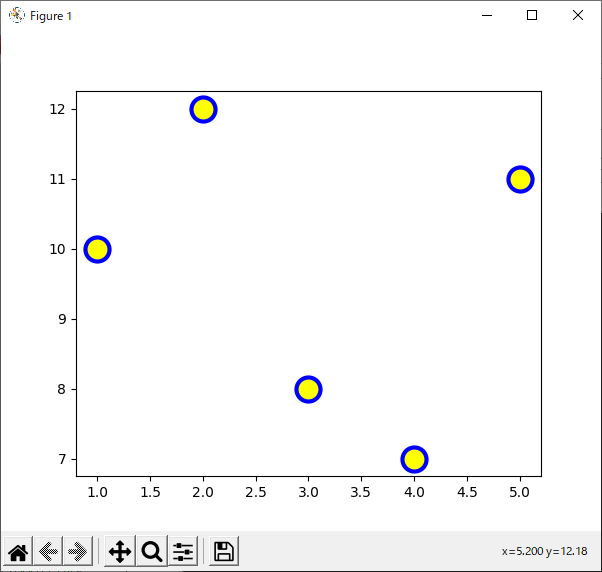
散布図を描くときは，“Axes.scatter()”メソッドを使います（リスト40）．

import matplotlib.pyplot as plt
import numpy as np

x = np.array( [1, 2, 3, 4, 5] )
y = np.array( [10, 12, 8, 7, 11] )

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.scatter(x, y, color="yellow", marker="o", s=300, edgecolors="blue", linewidths=3)

plt.show()

4行目と5行目で，散布図としてプロットする元データを用意しています．

10行目で“scatter()”メソッドを使って散布図を描画しています．第1引数には$x$座標のリスト“x”，第2引数には$y$座標のリスト“y”を渡します．

“color”キーワードでマーカーの塗りつぶし色，“marker”キーワードでマーカーの形状，“s”キーワードでマーカーのサイズを設定します．

“edgecolors”キーワードは輪郭の色，“linewidths”キーワードは輪郭の線幅を設定するためのものです．これらのキーワードには複数形の“s”が付くので注意してください．

リスト40のプログラムの実行結果を図44に示します．

図44　散布図を描いた様子

棒グラフを描く

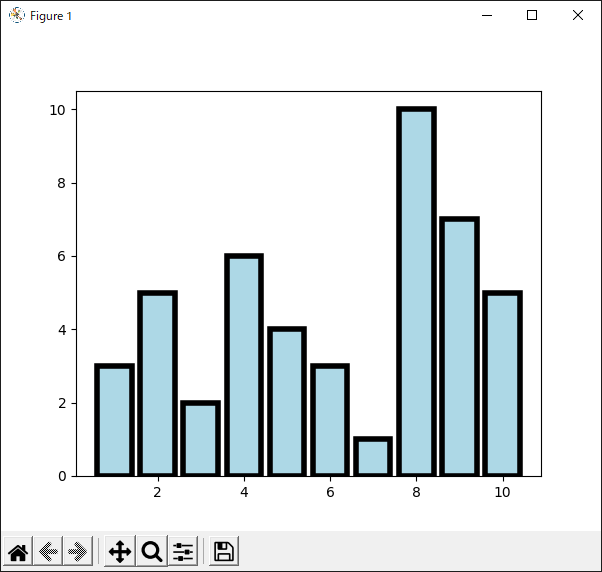
棒グラフを描くときは，“Axes.bar()”メソッドを使います（リスト41）．

import matplotlib.pyplot as plt
import numpy as np

x = np.array( [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] )
y = np.array( [3, 5, 2, 6, 4, 3, 1, 10, 7, 5 ] )

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.bar(x, y, width=0.8, color="lightblue", edgecolor="black", linewidth=4)

plt.show()

4行目と5行目では，棒グラフとしてプロットする元データを用意しています．

10行目の“bar()”関数で棒グラフを描画しています．第1引数は$x$座標，第2引数は棒グラフの高さです．

“width”キーワードで棒グラフの幅を設定します．“width=1.0”とすると棒グラフが隙間なく表示されます．“color”は棒グラフの色，“edgecolor”は輪郭の色，“linewidth”は輪郭の線幅を設定するためのキーワードです．

リスト41のプログラムの実行結果を図45に示します．

図45　棒グラフを描いた様子

ヒート・マップを描く

「ヒート・マップ」は，2次元平面上の各地点における値の大きさを「色」で表現したものです．Matplotlibでヒート・マップを表現する方法は何種類かありますが，ここでは“Axes.imshow()”メソッドを使う方法を紹介します．

“Axes.imshow()”でヒート・マップを描く

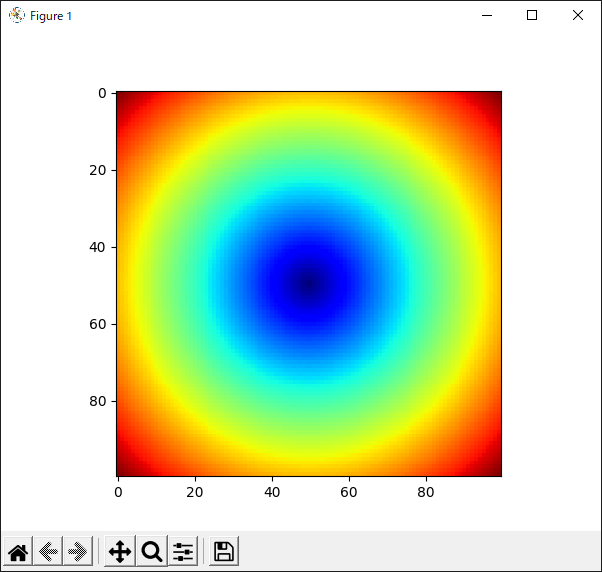
“Axes.imshow()”はグラフ領域（Axesオブジェクト）に画像を読み込んで表示するためのメソッドですが，2次元配列を渡せば値に応じたヒート・マップを表示することもできます（リスト42）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)

Z = np.sqrt(X**2 + Y**2)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.imshow(Z, cmap="jet")

plt.show()

4行目と5行目で$x$軸および$y$軸方向の座標のリストを作ります．これがメッシュの元になります．

6行目では“numpy.meshgrid()”関数を使い，2次元プロット用のメッシュを作っています．

8行目では，ヒート・マップとしてプロットするためのデータを作っています．今回は各地点における“$\sqrt{x^2 + y^2}$”の値を“Z”という2次元配列に格納しています．

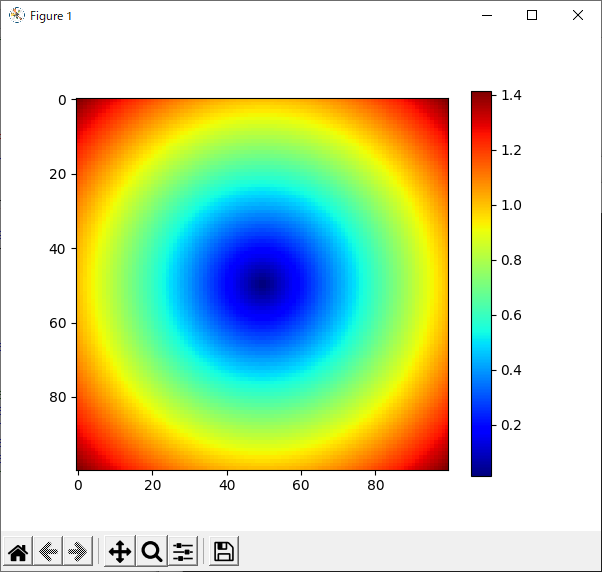
13行目で“imshow()”メソッドを使い，ヒート・マップを描画しています．第1引数はヒート・マップとして描画する2次元配列データです．また，“cmap”キーワードを使ってヒート・マップの色使いを定める「カラー・マップ」を指定します．Matplotlibで使用できるカラー・マップは“Choosing Colormaps in Matplotlib”のページを参照してください．

リスト42のプログラムの実行結果を図46に示します．

図46　ヒート・マップを描いた様子

カラー・バー付きのヒート・マップを描く

ヒート・マップに「カラー・バー」を付けるには，“Figure.colorbar()”を使います（リスト43）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)

Z = np.sqrt(X**2 + Y**2)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

heat_map1 = ax1.imshow(Z, cmap="jet")

fig.colorbar(heat_map1, ax=ax1)

plt.show()

13行目で“imshow()”メソッドを使ってヒート・マップを描画するときに，“imshow()”が返すオブジェクト（AxesImageオブジェクト）を“heat_map1”という変数に格納しています．

15行目では“Figure.colorbar()”メソッドを使い，カラー・バーを作成しています．第1引数には，さきほど“imshow()”メソッドが返したAxesImageオブジェクト“heat_map1”を渡しています．また，“ax”キーワードを使ってカラー・バーを取り付けるAxesオブジェクトを指定します．今回用意しているAxesオブジェクトは“ax1”だけなので指定しなくても構いませんが，複数のAxesオブジェクトがある場合は明示しておくとトラブルを防げます．

リスト43のプログラムの実行結果を図47に示します．

図47　カラー・バー付きのヒート・マップを描いた様子

なお，他のグラフ形式でも同様の方法でカラー・バーを設定できます．

等高線図を描く

等高線図を描くときは，“Axes.contour()”メソッドを使います．“contour”（カントゥア）は「輪郭」や「外形」，「等高線」といった意味の英単語です．

“Axes.contour()”メソッドで等高線を描く

さきほどヒート・マップを描いたのと同じデータを使って等高線図を描いてみます（リスト44）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 200)
y = np.linspace(-1, 1, 200)
X, Y = np.meshgrid(x, y)

Z = np.sqrt(X**2 + Y**2)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.contour(X, Y, Z, levels=20, cmap="jet")

ax1.set_aspect(1)

plt.show()

4行目から6行目では，2次元プロット用のメッシュを用意しています．

8行目では，等高線プロット用のデータを用意しています．これが「各地点の標高の高さ」を表すデータに相当します．

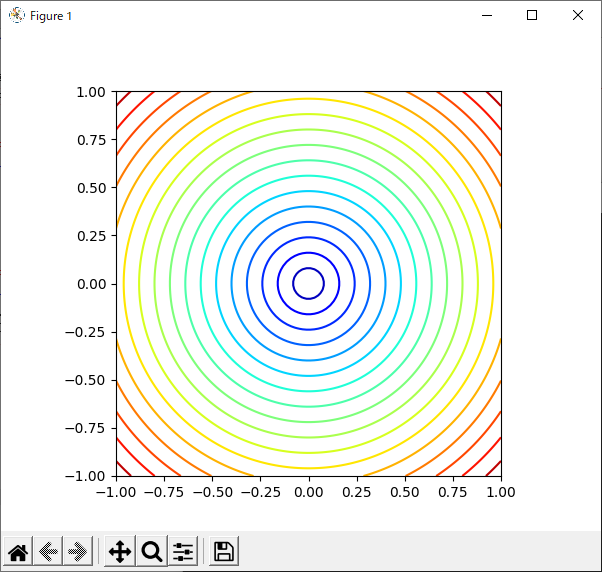
13行目では，“contour()”メソッドを使って等高線をプロットしています．第1引数は$x$座標のメッシュ，第2引数は$y$座標のメッシュです．第3引数に，等高線のもとになる「各地点の高さ」を表す2次元配列を渡します．

“levels”キーワードで等高線の本数の上限を設定します．今回は“levels=20”として，本数の上限を20本としました．等高線の本数は自動的に加減されるので，この“levels”で指定した値そのものにならない場合もあります．

なお，“levels=[1, 2, 3]”のように数値のリストを指定すると，高さ（今回は“Z”の値）がその値と一致する地点を結んだ等高線が描画されます．これは「陰関数」をプロットする時に便利です．

“cmap”キーワードでは，表示する際のカラー・マップを設定します．

15行目では，“Axes.set_aspect()”メソッドを使ってグラフ領域のアスペクト（縦横比）を設定しています．今回は縦と横を同じ長さにしたいので“1”としました．

リスト44のプログラムの実行結果を図48に示します．

図48　等高線図を描いた様子

“Axes.contourf()”メソッドで等高線（塗りつぶしあり）を描く

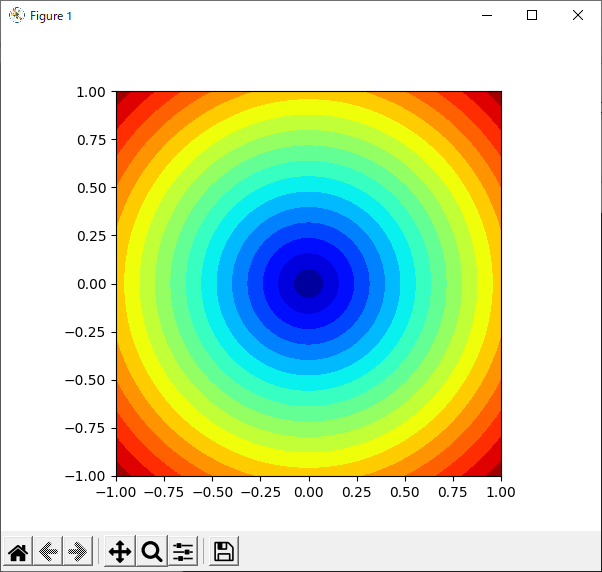
“Axes.contourf()”メソッドを使うと，色で塗り潰した等高線を描くことができます（リスト45）．“contourf”の“f”は“fill”（塗りつぶし）の略です．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)

Z = np.sqrt(X**2 + Y**2)

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.contourf(X, Y, Z, levels=20, cmap="jet")

ax1.set_aspect(1)

plt.show()

13行目で，“contourf()”メソッドを使って塗りつぶしありの等高線を描いています．引数の意味はさきほどの“contour()”メソッドと同じです．

リスト45のプログラムを実行した様子を図49に示します．

図49　塗りつぶしありの等高線図を描いた様子

ベクトル場を描く

“Axes.quiver()”メソッドを使うと，ベクトル場を描くことができます．“quiver”（クィバー）は「矢筒」という意味の英単語で，ベクトル場を表す矢印をたくさんプロットする様子から名付けられているものと思われます．

“Axes.quiver()”メソッドで1本のベクトルを描く

まずは“Axes.quiver()”メソッドを使って1本だけベクトルを描いてみます（リスト46）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.quiver(2, 1, 4, 2)

ax1.set_xlim(0, 6.5)
ax1.set_ylim(0, 3.5)
plt.show()

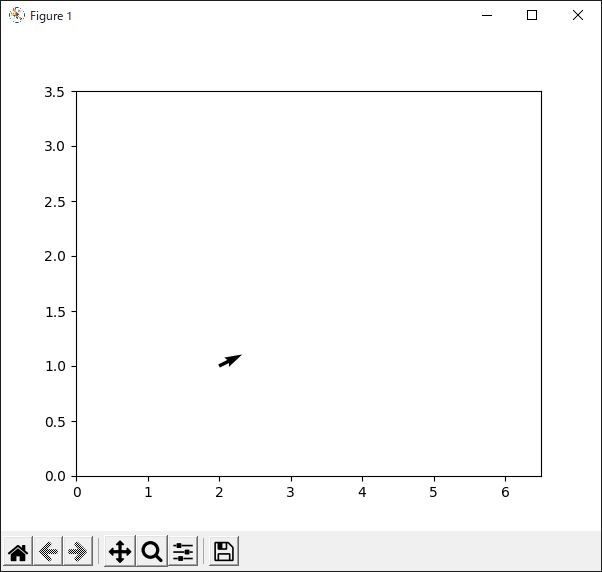
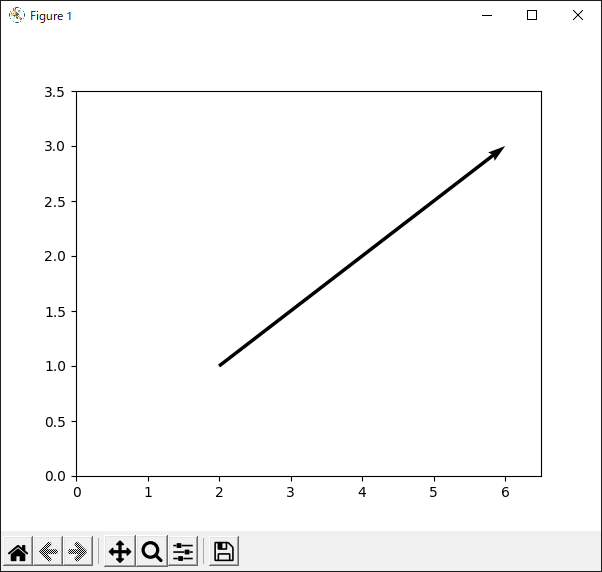
7行目で“quiver()”メソッドを使ってベクトルを描いています．第1引数はベクトルの始点の$x$座標，第2引数は始点の$y$座標です．また，第3引数はベクトルの$x$成分の大きさ，第4引数は$y$成分の大きさです．

今回は座標“(2, 1)”を始点として，成分が“(4, 2)”のベクトルを描画しています．よって，ベクトルの終点の座標は“(6, 3)”になると考えられます．

リスト46のプログラムの実行結果を図50に示します．

図50　1本のベクトルを描いた様子（座標軸を基準としたスケールになっていない）

ベクトルの始点の座標はソース・コードに書いたとおり “(2, 1)”となっていますが，終点の座標はおよそ“(2.3, 1.1)”となっており，実際に指定した“(6, 3)”から大きく外れています．この原因は「スケール」の設定にあります．デフォルトの場合，“quiver()”メソッドはベクトルが見やすくなるように「スケール」（縮尺）を自動的に調整します．この機能は便利ですが，今回のようにベクトルの大きさを忠実に表現したい場合は注意が必要です．

ベクトルの大きさを実物大で表示する

次は，与えた成分の大きさにしたがって忠実にベクトルを描画してみます（リスト47）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.quiver(2, 1, 4, 2, angles="xy", scale_units="xy", scale=1.0)

ax1.set_xlim(0, 6.5)
ax1.set_ylim(0, 3.5)
plt.show()

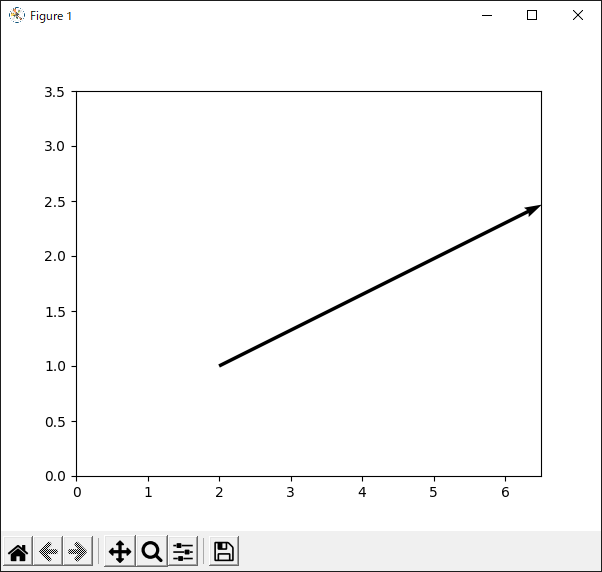
今回は，7行目で“quiver()”メソッドを実行するときにいくつか新しいキーワードを与えて，原寸大のスケールで表示するようにしています．

“angles”キーワードは，「ベクトルの角度」（$x$成分と$y$成分の比，つまりタンジェント）の基準を設定するために使います．デフォルトでは“uv”モードになっており，「グラフ領域（Axesオブジェクト）の幅と高さ」を基準として描画します．一方で，今回設定している“xy”モードでは「座標軸上の値」を基準として描画します．

“scale_units”と“scale”キーワードは，「ベクトルの長さ」の基準を設定するために使います．今回のように“scale_units”を“xy”，“scale”を“1.0”に設定すると，与えた成分の大きさが座標軸と整合するように描画されます．

なお，ベクトルの長さは「もともとの矢印の長さを“scale”で割った値」となるので，“scale”を小さくするほどベクトルは長くなります．

リスト47のプログラムの実行結果を図51に示します．

図51　1本のベクトルを描いた様子（座標軸を基準としたスケールで表示）

ベクトルの終点が“(6, 3)”になっていることが確認できます．よって，リスト47のように“angles”，“scale_units”，“scale”を設定すれば，ベクトルの大きさが与えられた成分のとおりに描画されることがわかります．

“angles”の設定を“uv”にしたときの挙動

実験として，“angles”キーワードで“uv”を指定した場合の挙動を見てみます（リスト48）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.quiver(2, 1, 4, 2, angles="uv", scale_units="xy", scale=1.0)

ax1.set_xlim(0, 6.5)
ax1.set_ylim(0, 3.5)
plt.show()

今回は7行目で“quiver()”メソッドを呼ぶときに，“angles”キーワードで“uv”を指定しています．それ以外の設定はさきほどのプログラムと同じです．

リスト48のプログラムの実行結果を図52に示します．

図52　“angles”を“uv”に設定すると，ウィンドウ・サイズを変えたときにベクトルの成分の大きさが変わってしまう

与えた成分通りに描画すればベクトルの終点が“(6, 3)”となるはずですが，今回は違う値になっています．ここで，Matplotlibで表示したグラフのウィンドウ・サイズを変えると，それにともなってベクトルの寸法が変わってしまいます．このことから，“angles”キーワードで“uv”を指定した場合は「座標軸ではなく描画領域の寸法を基準にしてベクトルの大きさを決めている」ことがわかります．

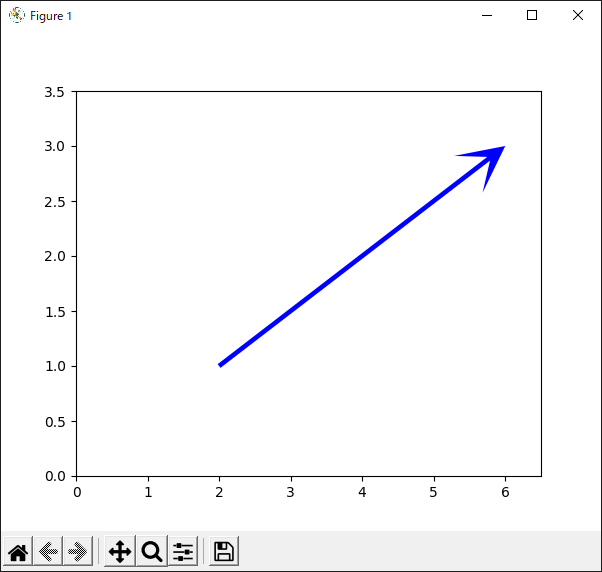
ベクトルの色や大きさを設定する

ベクトルの見栄えを調整します（リスト49）．

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.quiver(2, 1, 4, 2, angles="xy", scale_units="xy", scale=1.0, color="blue", width=0.01, headlength=10, headwidth=10)

ax1.set_xlim(0, 6.5)
ax1.set_ylim(0, 3.5)
plt.show()

7行目では，“quiver()”メソッドを呼ぶ際にベクトルの見栄えを調整するキーワードを与えています．

「ベクトルの色」を変える場合は“color”キーワードを使います．

「ベクトルの長さ」は，さきほど実験したように“scale”キーワードで設定します．

「ベクトルの太さ」（直線部分の線幅）は“width”キーワードで設定します．デフォルトはおよそ“0.005”です．

「矢印部分の長さ」は“headlength”キーワードで設定します．デフォルトは“5”です．矢印部分の長さは「軸の部分の太さの何倍か」という表現方法になっているので，“width”の値を変更すると矢印部分の長さも同時に変化します．

「矢印部分の幅」は“headwidth”キーワードで設定します．デフォルトは“3”です．これも「軸の部分の太さの何倍か」という形で定義されています．

リスト49のプログラムの実行結果を図53に示します．

図53　ベクトルの見栄えを調整した様子

2次元のベクトル場を描く

メッシュを用意して，2次元のベクトル場を描画してみます．

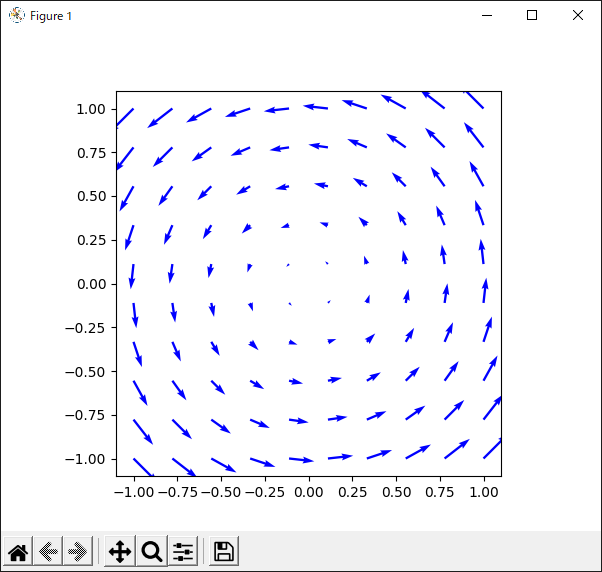
ここでは，位置“$(x, y)$”におけるベクトル場“$\bm{A}(x,y)=(A_x(x,y), A_y(x,y))$”を「その地点を指す位置ベクトル“$(x, y)$”を90度回転させたもの」として定義します．これは，いわゆる「回転行列」を使うと次のように表せます．

上式より，ベクトル場“$\bm{A}$”の$x$成分は“$A_x = -y$”，$y$成分は“$A_y = x$”となります．これを描画するプログラムはリスト50のようになります．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 10)
y = np.linspace(-1, 1, 10)
X, Y = np.meshgrid(x, y)

A_x = -Y
A_y = X

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.quiver(X, Y, A_x, A_y, angles="xy", color="blue")

ax1.set_aspect(1)

plt.show()

4行目から6行目で，2次元プロット用のメッシュを用意しています．

8行目と9行目で，ベクトル場“$\bm{A}$”の$x$成分と$y$成分を作っています．

14行目で“quiver()”メソッドを使い，ベクトル場を描画しています．第1引数は$x$座標用のメッシュ，第2引数は$y$座標用のメッシュです．第3引数は描画するベクトル場の$x$成分で，第4引数はベクトル場の$y$成分です．今回は“angles”を“xy”に設定しました．また，スケールはデフォルトのままです（適当な縮尺で表示される）．

16行目では，“set_aspect()”メソッドを使ってグラフ描画領域のアスペクトを“1:1”に設定しています．

リスト50のプログラムを実行した様子を図54に示します．

図54　ベクトル場を描いた様子

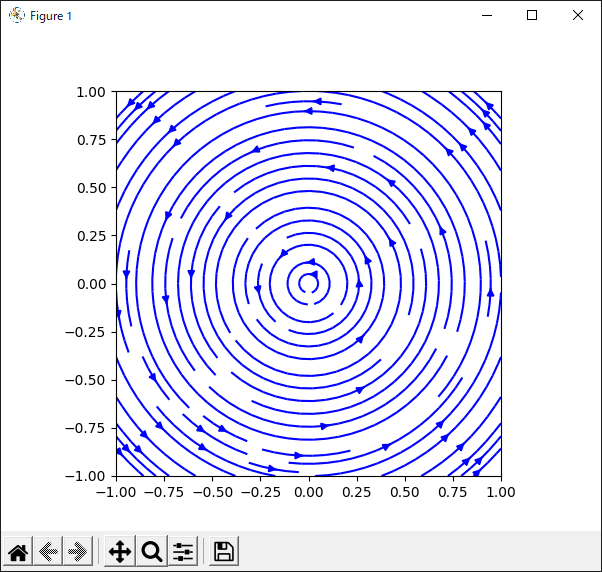
流線図を描く

流線図を描くときは，“Axes.streamplot()”メソッドを使います（リスト51）．

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 10)
y = np.linspace(-1, 1, 10)
X, Y = np.meshgrid(x, y)

A_x = -Y
A_y = X

fig = plt.figure( figsize=(6,5) )
ax1 = fig.add_subplot(1,1,1)

ax1.streamplot(X, Y, A_x, A_y, color="blue")

ax1.set_aspect(1)

plt.show()

4行目から6行目でメッシュを作り，8行目と9行目でベクトル場を用意しています．ここまでは“quiver()”のときと同じです．

14行目で“streamplot()”メソッドを使い流線図を描いています．第1引数はメッシュの$x$座標，第2引数はメッシュの$y$座標です．第3引数はベクトル場の$x$成分，第4引数はベクトル場の$y$成分です．また，“color”キーワードで流線の色を指定しています．

リスト51のプログラムを実行した様子を図55に示します．

図55　流線図を描いた様子