スピードマスタ・シリーズ
プロの技術を1日で！実習キット付きVOD

［VOD/KIT］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門

マイコンに組み込んだ物理モデルに倒立ロボットを自動操縦させる

関連製品：［VOD］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門
関連製品：［VOD/KIT］実習キットでできる！ラズパイPico×Wi-FiモジュールでIoT超入門
関連製品：［VOD］Pythonで学ぶやりなおし数学塾1【微分・積分】
関連製品：［VOD］Pythonで学ぶやりなおし数学塾2【フーリエ解析】
関連製品：［VOD］Pythonで学ぶマクスウェル方程式【電場編】＋【磁場編】
関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング基礎編/応用編
関連記事：Pythonではじめる数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
関連記事：Pythonではじめる数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]

本VOD製品を購入された方へ　～視聴リンクとパスワード～

VOD製品を購入された方は，以下のリンクからご覧いただけます．

キットの組み立て手順書はこちら
Part1:初等関数と微分・積分
Part2:線形代数
Part3:力学
Part4:現代制御理論
Part5:確率・統計
Part6:カルマン・フィルタ
Part7:フーリエ解析

VODサンプル


800分超の講義ビデオと約700頁の講義テキスト	プログラミング実習用「確率・統計ロボティクス学習キット」付き

自動運転やロボットの高精度自動制御の基礎を学ぶ

数百円のワンチップ・マイコンで確率・統計処理できる時代

真値を高速に推定するカルマン・フィルタは，マイコンなどの小さなコンピュータでも十分に処理できる軽い信号処理アルゴリズムです．自動走行する自動車やロケットの姿勢制御，高精度なGPS測位，株式/マーケティング予想，データ・サイエンス/人工知能まで，人に代わって動く無人の組み込みシステムに導入されています．

本VODでは，カルマン・フィルタを構成するために必要な数学を基礎から丁寧に解説します．さらに，マイコン・スタータキット“Nucleo”（STマイクロエレクトロニクス製）にカルマン・フィルタのプログラムを実装します．完成した倒立振子が動作する様子を見れば，「理論とはここまで強力なものなのか！」と実感できるでしょう．

受講対象

エンジニアリングで共通して使われる「数学」を学びたい方
ロボット制御の手法である「現代制御理論」を理解したい方
一般的な「モデル・ベース開発」の考え方を理解したい方
真値推定アルゴリズム「カルマン・フィルタ」を理解したい方

Index

Part1:初等関数と微分・積分

「関数」，「微分・積分」，「線形代数」という3つの分野は，ロボット設計，ディジタル信号処理，電子回路設計など，あらゆる理工学の基礎になっています．Part1では，まず「初等関数」と「微分・積分」の基礎理論を丁寧に解説します．

講義テキストのサンプルを見る

イントロダクション
統計学の面白さ/「統計的推定」を行う信号処理
初等関数
多項式関数・有理関数/三角関数/指数関数/対数関数
微分・積分/1変数関数の微分
1変数関数の積分/オイラーの公式/2変数関数の微分/2変数関数の積分/ガウス積分

Part2:線形代数

線形代数の基本や線形システムの利点を解説します．線形代数は，後で解説する「現代制御理論」の基礎となります．

講義テキストのサンプルを見る

入力・出力がある「システム」を考える
線形システムの利点
線形代数/ベクトル/行列/行列式/行列と連立1次方程式/固有値と固有ベクトル/対称行列と2次形式

Part3:力学

力学を学ぶと，ロボットなどの物体の動き方を理解したり予測したりできるようになります．Part3では，「ニュートンの運動方程式」から，力学モデルを作るときに役立つ「ラグランジュの運動方程式」，倒立振子のモデル作成例まで，体系的にわかりやすく解説します．

講義テキストのサンプルを見る

イントロダクション
「力学」のキー・ポイント/「運動」のとらえかた
力学
ニュートンの運動方程式/オイラーの回転運動方程式/剛体の運動/回転座標系とコリオリカ
解析力学
倒立振子のモデル作成例

Part4:現代制御理論

現代制御理論の特徴は，複数の値を同時に扱えることです．この複数の値を同時にフィードバックすることを「状態フィードバック」といいます．状態フィードバックで使うフィードバック・ゲインを効率良く求める手法を「最適制御」といいます．Part4では，システムの安定化に利用される状態フィードバックや最適制御などの制御理論を解説します．ここで説明する状態方程式は，カルマン・フィルタの理解にもつながります．

講義テキストのサンプルを見る

現代制御理論のキー・ポイント
状態方程式
可制御性と可観測性
安定性
状態フィードバック
オブザーバ
最適制御

Part5:確率・統計

確率・統計は，IoTにおけるセンサ・データの解析，AI，電子回路，土木・建築など多くの分野で広く活用されています．Part5では統計学全般で重要な役割を果たす「正規分布」をわかりやすく解説します．

講義テキストのサンプルを見る

確率・統計のキー・ポイント
記述統計
確率の基礎
確率変数と確率分布
2次元の確率分布
正規分布
中心極限定理

Part6:カルマン・フィルタ

無人機やロボットが目的地に向かって走行したり航行したりするには，自分自身の「位置」や「姿勢」を正確に知ることが重要です．しかし，センサによる測定値には必ず誤差が含まれます．カルマン・フィルタは，センサの測定値から誤差を取り除くための技術です．Part6では，自動運転をはじめとする高精度自動制御やデータ解析の分野におけるキー・テクノロジ「カルマン・フィルタ」の理論を基礎から解説します．

講義テキストのサンプルを見る

イントロダクション
カルマン・フィルタのキー・ポイント/カルマン・フィルタの動作
時系列データ
最大事後確率推定(1変数)
カルマン・フィルタの導出(1変数)

Part7:フーリエ解析

フーリエ解析は，信号処理，電子回路，線形システムなどの工学分野に広く利用されている数学的手法です．Part7では，フーリエ解析の考え方の要点をわかりやすく解説します．

講義テキストのサンプルを見る

「電気」に関する微分方程式：マクスウェル方程式
インダクタとキャパシタの挙動
交流回路理論
フーリエ変換
フーリエ変換と線形性
「微分方程式」を「代数方程式」にする
ラプラス変換
$z$変換

プログラミング実習用「確率・統計ロボティクス学習キット」付き

物理法則にもとづくモデルをマイコンに組み込んで操縦させる

1969年，アメリカ航空宇宙局 NASAは38万kmのかなたにある月に宇宙船「アポロ11号(写真1)」をコンピュータで誘導し，無事に着陸させることに成功しました．

アポロ11号のコンピュータ(写真2)は，わずか70行程度のプログラムを利用して宇宙船の位置や姿勢を正確に算出していました．「数理モデル」と「実測値」を利用して確率統計処理によって雑音(誤差)を最小化し，最も確からしい値を短時間で推定する「カルマン・フィルタ」です．

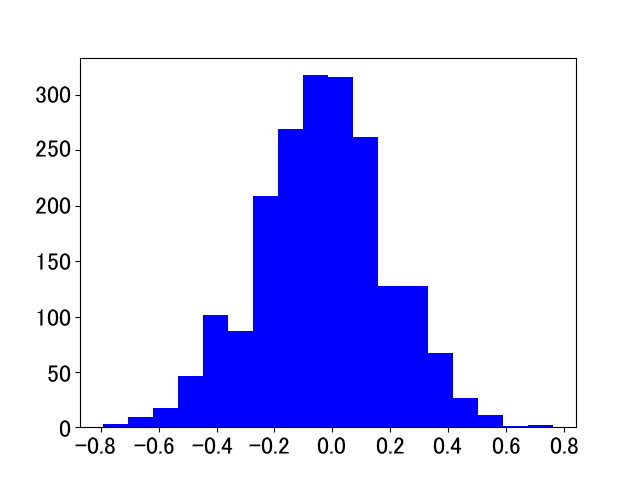
どんなセンサの値にも，「誤差」や「ゆらぎ」といった不要な成分が含まれています．センサの出力値の統計をとると，おおよそ図1のような「正規分布」が得られます．この正規分布の中心が「本当の値」すなわち「真値」であると考えられます．

たくさんのデータの平均をとれば「正規分布の中心」を求められそうですが，実際のリアルタイム処理では図1のように大量のデータを実測するのは困難です．そこで確率・統計の考え方を利用して「真値」にアプローチしようというのが，カルマン・フィルタのアイディアです．カルマン・フィルタを利用すれば，少ないデータをもとにして短時間で「真値」を推定することができます．

アポロ11号が搭載したアルゴリズムは，いわゆるAI（人工知能）の原型ともいえるものです．最近のAIには様々なアルゴリズムがありますが，その中でも教師データを読み込ませてニューラル・ネットワーク上に一種のモデルを構築するという方法がよく知られています．アポロ11号で用いられたカルマン・フィルタにも「計算モデル」は搭載されていましたが，それは自動的な学習によって生成されたものではなく，科学者が自ら用意した「物理モデル」でした．宇宙船に組み込まれたカルマン・フィルタは，「手作業で作ったモデルにもとづいて確率的にもっとも正しそうな値を探すアルゴリズム」ということになります．

1969年当時のコンピュータは何億円もした大がかりなものでしたが，現在は数百円で遥かに高性能なワンチップ・マイコンが手に入ります．今のワンチップ・マイコンを使えば，カルマン・フィルタの処理を十分高速に処理することができます．このキットはカルマン・フィルタによる処理を体験し，その動作原理を理解するために大いに役立ちます．


写真1: 1969年，NASAは，コンピュータ誘導によって，有人宇宙船「アポロ11号」38万km先にある月まで正確に誘導し着陸させた	写真2: アポロ11号に搭載された誘導用コンピュータ“AGC(Apollo Guidance Computer)”	図1: センサによる測定を何度も繰り返すと正規分布が得られる

カルマン・フィルタのアルゴリズム

カルマン・フィルタのアルゴリズムは，基本的に4本の数式で表されます．本プログラミング実習キット「確率・統計ロボティクス学習キット」では，この計算をマイコン上で実行してロボットの姿勢推定を行っています．具体的なプログラム例は本ページの末尾に掲載しています．

（1）共分散行列の更新

\begin{equation} P_0 = \left(P_{0}^{\prime -1} -C^{T}W^{-1}C \right)^{-1} \end{equation}

（2）真値の推定値の計算

\begin{equation} \hat{\bm{x}}_0 = \tilde{\bm{x}}_0 + P_0 C^{T} W^{-1} \left( \bm{y}_0 -C \tilde{\bm{x}}_0 \right) \end{equation}

（3）1ステップ先の共分散行列の予測

\begin{equation} P_1^{\prime} = AP_0 A^{T} + BUB^{T} \end{equation}

（4）1ステップ先の予測値の計算

\begin{equation} \tilde{\bm{x}}_1 = A\hat{\bm{x}}_0 + B \bm{u}_0 \end{equation}

プログラミング実習キット「確率・統計ロボティクス学習キット」の仕様


写真3: 確率・統計ロボティクス学習キット MZIP-01

本VODに付属する確率・統計ロボティクス学習キット MZIP-01(写真3)の制御には，「最適制御」を利用しています．姿勢推定には「カルマン・フィルタ」を使っています．

確率・統計ロボティクス学習キットを設計・製作する一連の流れをたどれば，ロボット制御のための基本的な考え方をひととおり身に着けることができます．完成した倒立振子が動作する様子を見れば，「理論とはここまで強力なものなのか！」と実感できるでしょう．

プログラミング実習キット「確率・統計ロボティクス学習キット」の設計方針

本VODに付属する確率・統計ロボティクス学習キットの設計方針を以下に示します．

理論を学び理解するための道具として設計・製作を行う
最低限の機能にしぼり，シンプルな構成とする
部品は通販で入手しやすく，できるだけ安価なものを選ぶ
「むやみやたらなチューニング」は極力避け，「設計」による一発動作を目指す

確率・統計ロボティクス学習キットは，とてもシンプルなものです．このロボットを設計・製作するノウハウを十分に理解すれば，自力でより複雑かつ多機能なものへ拡張できます．

マイコンはNUCLEO-F401REボードを使う

本キットは， “STM32F401RET6”というマイコン(以下，STM32F401)が実装されたNUCLEO-F401REボード(写真4)を搭載しています．

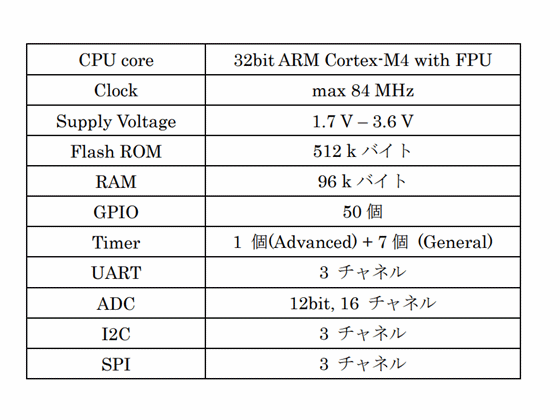
表1に，STM32F401マイコンの仕様を示します． STM32F401には豊富な周辺モジュールが搭載されていますが，いくつかのGPIO(“General Purpose Input/Output”，汎用入出力)とタイマ，UART，I$^2$Cモジュールだけを使います．そのため，違うマイコンを使っても問題なく実験を進められます．

STM32F401自体の電源電圧は1.7Vから3.6Vとなっていますが，NUCLEOボード上には電圧レギュレータが実装されているので，より広い範囲の電源電圧を印加できます．今回はニッケル水素蓄電池を4本使用して，4.8V(≒5V)を供給することにします．


写真4: すぐに開発を始められるNUCLEO-F401REボードを採用	表1: 姿勢の計測とカルマン・フィルタによる真値推定,モータ制御に使用したSTM32F401マイコンの仕様

NUCLEO-F401REボードはmbedのプラットフォームに登録されているので，開発環境を構築する手間を一気に省くことができます． NUCLEO-F401REボードとUSBケーブル(mini B-Type A)，そしてインターネットに接続されたPCがあればマイコンの開発環境が整います．なお，mbedを利用するには無料の会員登録が必要です．

確率・統計ロボティクス学習キットの部品表と回路図

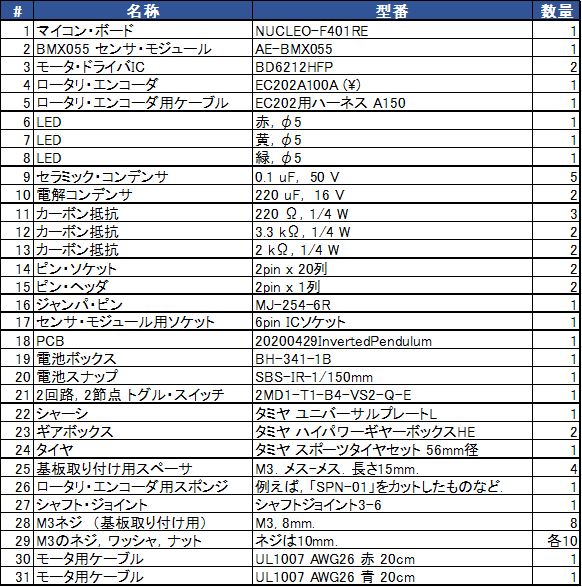
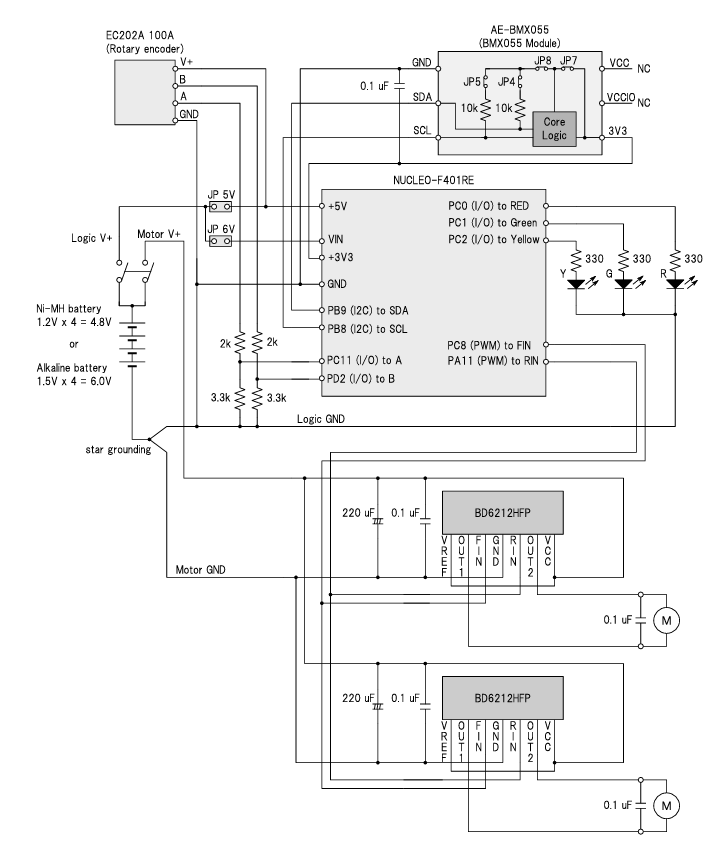
表2に，確率・統計ロボティクス学習キットの部品リストを，図2に回路図を示します．組み立て方は，組立説明書を参照ください．


表2: 確率・統計ロボティクス学習キット MZIP-01の部品表


図2: 確率・統計ロボティクス学習キット MZIP-01の回路図

確率・統計ロボティクス学習キットのシステム図

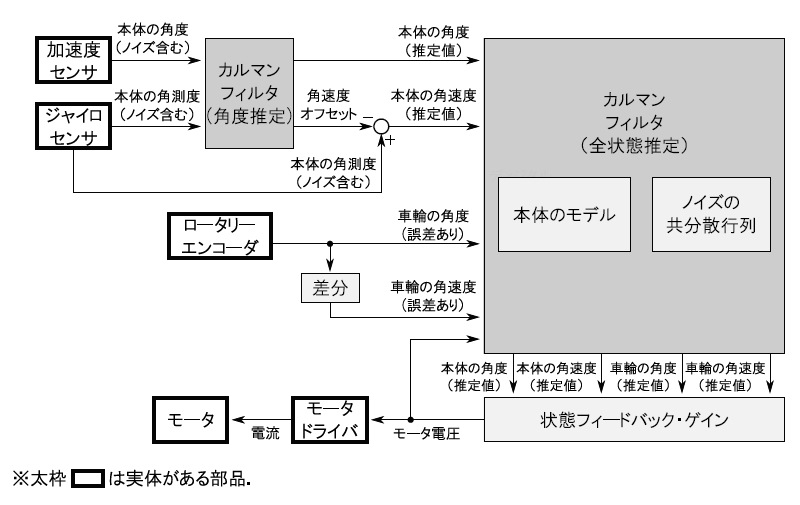
図3に，確率・統計ロボティクス学習キットの全システムを示します．太枠のブロックは実体がある部品を，それ以外はプログラム上の処理を表しています．

確率・統計ロボティクス学習キットには，2つのカルマン・フィルタが搭載されています． 1つめは加速度センサとジャイロ・センサの値を統合して，真の車体の傾斜角を推定するためのカルマン・フィルタです． 2つめは各センサの値およびモータ電圧にもとづいて，本体の姿勢(本体の角度，本体の角速度，車輪の角度，車輪の角速度)を推定するためのカルマン・フィルタです．

1つめのカルマン・フィルタは本体の角度をより正確に知るために使い， 2つめのカルマン・フィルタは本体を直立させる制御をより安定させるために使います．


図3: 確率・統計ロボティクス学習キットのシステム・ブロック図

プログラミング言語について

確率・統計ロボティクス学習キットのマイコン用プログラムは，C言語（厳密にはC++）で記述しています．

下記のソース・コードは，カルマン・フィルタの中核部分の抜粋です（ここでは全体としての計算量を減らすために「カルマン・ゲイン」を経由した計算を採用しています）．本キットのマイコンでは，この計算を10 msecの周期（100回/秒）で実行しています．

//---------------------------------------
//Kalman Filter (all system)
//---------------------------------------
//calculate Kalman gain: G = P'C^T(W+CP'C^T)^-1
mat_tran(C_x[0], tran_C_x[0], 4, 4);//C^T
mat_mul(P_x_predict[0], tran_C_x[0], P_CT[0], 4, 4, 4, 4);//P'C^T
mat_mul(C_x[0], P_CT[0], G_temp1[0], 4, 4, 4, 4);//CPC^T
mat_add(G_temp1[0], measure_variance_mat[0], G_temp2[0], 4, 4);//W+CP'C^T
mat_inv(G_temp2[0], G_temp2_inv[0], 4, 4);//(W+CP'C^T)^-1
mat_mul(P_CT[0], G_temp2_inv[0], G[0], 4, 4, 4, 4); //P'C^T(W+CP'C^T)^-1

//x_data estimation: x = x'+G(y-Cx')
mat_mul(C_x[0], x_data_predict[0], C_x_x[0], 4, 4, 4, 1);//Cx'
mat_sub(y[0], C_x_x[0], delta_y[0], 4, 1);//y-Cx'
mat_mul(G[0], delta_y[0], delta_x[0], 4, 4, 4, 1);//G(y-Cx')
mat_add(x_data_predict[0], delta_x[0], x_data[0], 4, 1);//x'+G(y-Cx')

//calculate covariance matrix: P=(I-GC)P'
mat_mul(G[0], C_x[0], GC[0], 4, 4, 4, 4);//GC
mat_sub(I4[0], GC[0], I4_GC[0], 4, 4);//I-GC
mat_mul(I4_GC[0], P_x_predict[0], P_x[0], 4, 4, 4, 4);//(I-GC)P'

//predict the next step data: x'=Ax+Bu
Vin = motor_value;
if(motor_value > vdd_voltage)

{
    Vin = vdd_voltage;
}
if(motor_value < -vdd_voltage)
{
    Vin = -vdd_voltage;    
}
mat_mul(A_x[0], x_data[0], A_x_x[0], 4, 4, 4, 1);//Ax_hat
mat_mul_const(B_x[0], Vin , B_x_Vin[0], 4, 1);//Bu
mat_add(A_x_x[0], B_x_Vin[0], x_data_predict[0], 4, 1);//Ax+Bu 

//predict covariance matrix: P'=APA^T + BUB^T
mat_tran(A_x[0], tran_A_x[0], 4, 4);//A^T
mat_mul(A_x[0], P_x[0], AP[0], 4, 4, 4, 4);//AP
mat_mul(AP[0], tran_A_x[0], APAT[0], 4, 4, 4, 4);//APA^T
mat_tran(B_x[0], tran_B_x[0], 4, 1);//B^T
mat_mul(B_x[0], tran_B_x[0], BBT[0], 4, 1, 1, 4);//BB^T
mat_mul_const(BBT[0], voltage_variance, BUBT[0], 4, 4);//BUB^T
mat_add(APAT[0], BUBT[0], P_x_predict[0], 4, 4);//APA^T+BUB^T

本VOD製品を購入された方へ　～視聴リンクとパスワード～

講義テキストと講義ビデオは，著作権保護のためパスワードがかけられています．下記リンク先(青字)をクリックして，同梱の説明書に書かれたパスワードを入力してください．

キットの組み立て手順書とプログラム

Part4:現代制御理論

Part5:確率・統計

講義テキスト：カルマン・フィルタ入門_Part5_確率・統計.pdf
講義ビデオ：カルマン・フィルタ入門_Part5_確率・統計.mp4

Part6:カルマン・フィルタ

講義テキスト：カルマン・フィルタ入門_Part6_カルマン・フィルタ.pdf
講義ビデオ：カルマン・フィルタ入門_Part6_カルマン・フィルタ.mp4

Part7:フーリエ解析

講義テキスト：カルマン・フィルタ入門_Part7_フーリエ解析.pdf
講義ビデオ：カルマン・フィルタ入門_Part7_フーリエ解析.mp4

講師紹介

詳細はこちらを参照ください．

略歴

2011年　東京工業大学工学部　電気電子工学科　卒業
2013年　東京工業大学大学院理工学研究科　電子物理工学専攻　修了
2013年　株式会社アドバンテスト　入社
2016年　株式会社村田製作所　入社
2019年　リニア・テック　開業

主な著書

電子回路のキホン要点マスタ50，トランジスタ技術，2015年5月号，別冊付録，CQ出版社．
情熱のフル・ディスクリートFMラジオ，トランジスタ技術，2016年1月号　特集　第5章，CQ出版社．
本質理解！万能アナログ回路塾，トラジスタ技術，2017年9月号，連載，CQ出版社．
初等関数と微分・積分，2019年，CQ出版社．
月着陸船アポロに学ぶ確率統計コンピュータ，トランジスタ技術，2019年7月号　特集，CQ出版社．
大解剖！CPUはこうやって動いている，トランジスタ技術，2020年5月号　特集，CQ出版社．

プロの技術を1日で！
実習キット付き講義動画「スピードマスタ・シリーズ」

電子回路・基板設計からプログラミングまで，エンジニアがマスタすべき技術は多岐にわたり，開発期間も短くなっています．多くの書物を読み漁ったり，玉石混交のネット情報に振り回されたりしている暇はありません．

本シリーズには，各分野の一線で活躍する技術者が厳選したパーツセット，設計の要点を効率よく解説するセミナ動画，講義テキスト，お手本ソースコードなどが同梱されています．百戦錬磨の技を一見することで，未経験の技術が驚くほど短時間で身につくだけでなく，信頼性の高いシステム開発に必要なプロの眼が養われます．

［VOD/KIT］確率・統計処理＆真値推定！自動運転時代のカルマン・フィルタ入門

本VOD製品を購入された方へ ～視聴リンクとパスワード～

VODサンプル

自動運転やロボットの高精度自動制御の基礎を学ぶ

数百円のワンチップ・マイコンで確率・統計処理できる時代

受講対象