スピードマスタ・シリーズ
プロの技術を1日で！実習キット付きVOD

［VOD］Pythonで学ぶやりなおし数学塾2【フーリエ解析】

フーリエ級数の基礎からフーリエ変換，ラプラス変換，線形システムの伝達関数まで

関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング基礎編/応用編
関連製品：［VOD］Pythonで学ぶやりなおし数学塾1【微分・積分】
関連製品：［VOD］Pythonで学ぶやりなおし数学塾2【フーリエ解析】
関連製品：［VOD］Pythonで学ぶマクスウェル方程式【電場編】＋【磁場編】
関連記事：Pythonではじめる数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
関連記事：Pythonではじめる数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]


「インパルス応答」の畳み込み積分によってシステムの出力を得る様子	sin関数を足し合わせて矩形波を作る「フーリエ級数」	周波数が異なるsin関数どうしは「直交」している

あらまし

電気回路設計，機械設計，制御システム設計，データ処理，プログラミングといった様々な技術分野において，「数学」は非常に汎用的かつ便利な道具です．「Pythonで学ぶやりなおし数学塾」シリーズでは，数学的な考え方の本質をPythonプログラムでわかりやすく視覚化しながら丁寧に解説します．

テーマは「フーリエ解析」です．フーリエ解析は，物理学やエンジニアリングの各分野でよく使われる「微分方程式を解く技法」をまとめた体系です．「なぜ物理学や工学の本には三角関数ばかり出てくるのか？」，「周波数軸で物を見ると何が良いのか？」，「フーリエ変換とラプラス変換の共通点・相違点とは？」，「インパルス応答とは何なのか？」，「畳み込み積分とは何なのか？」といった素朴な疑問にわかりやすく答えます．


ラプラス変換の本質的な意味	「ラプラス変換」を使って電気回路を設計する

解説項目

（1）フーリエ級数の導入

正弦波が特別な理由
関数どうしの内積
三角関数の直交性
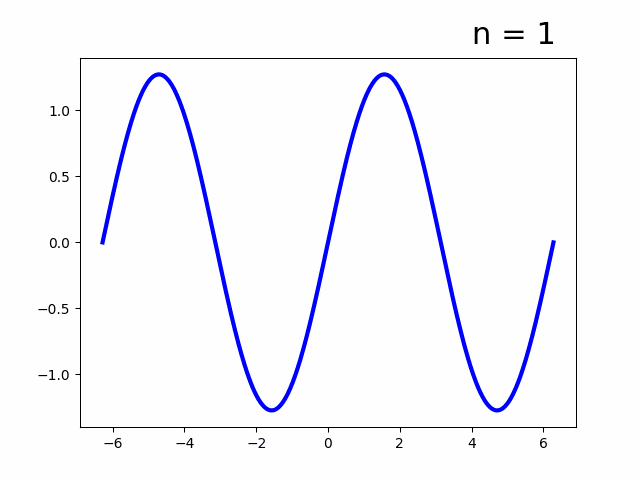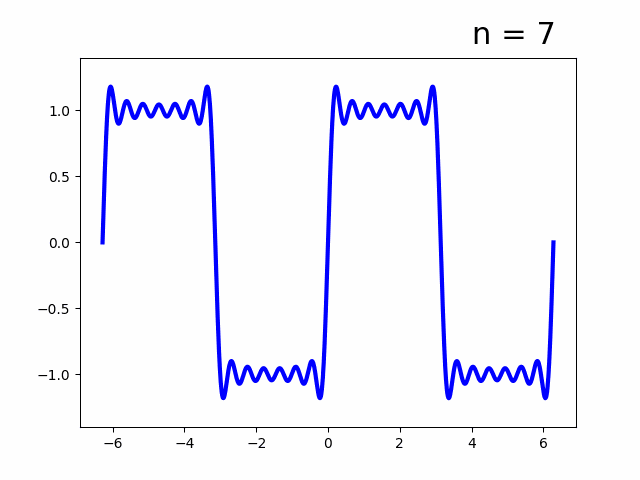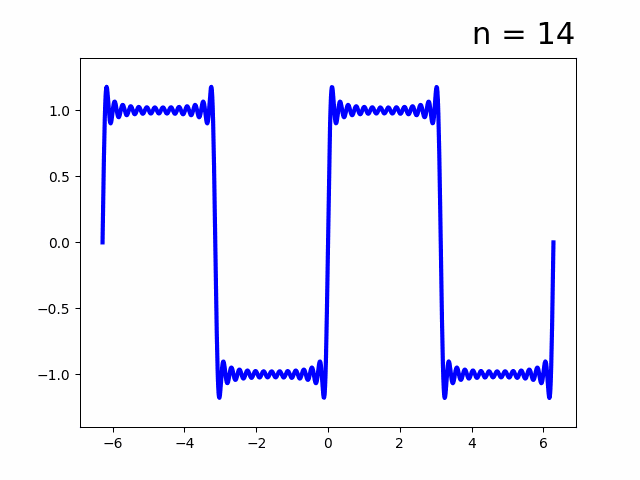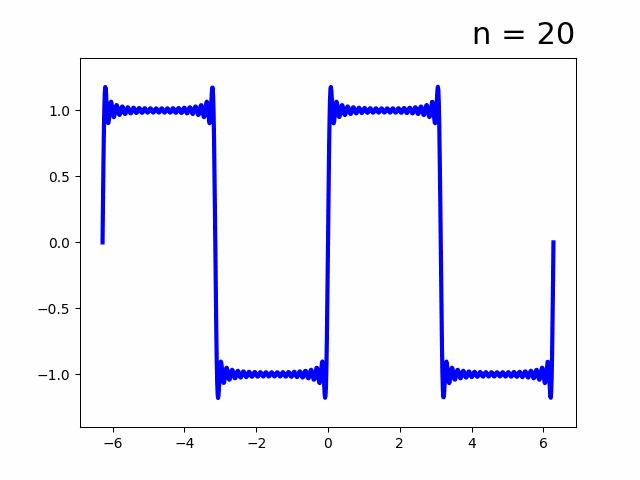
実フーリエ級数
複素フーリエ級数
Pythonプログラムで「直交」を体感するアニメーションをPythonで作る

（2）フーリエ変換とラプラス変換

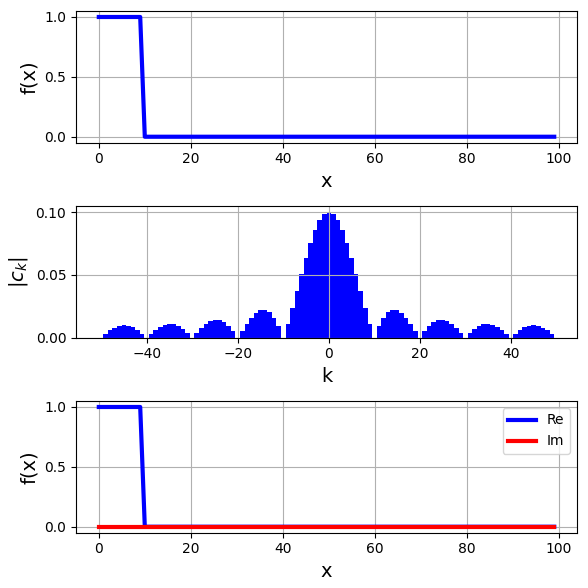
フーリエ変換
畳み込み積分
ラプラス変換
デルタ関数
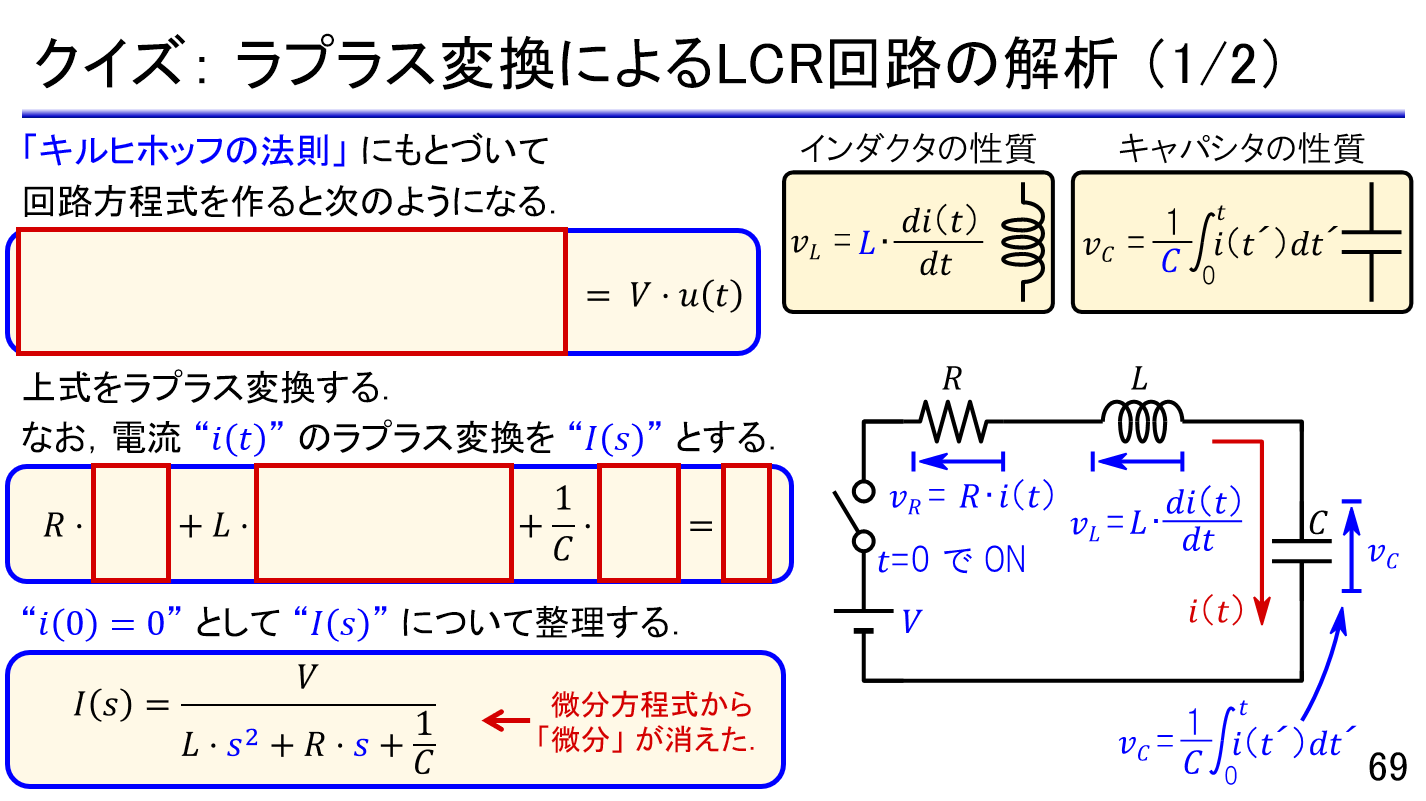
フーリエ解析を活用して微分方程式を解く方法
フーリエ変換（DFT）およびフーリエ逆変換（IDFT）を実行するPythonプログラム

（3）電気回路設計，制御理論，信号処理などへの応用

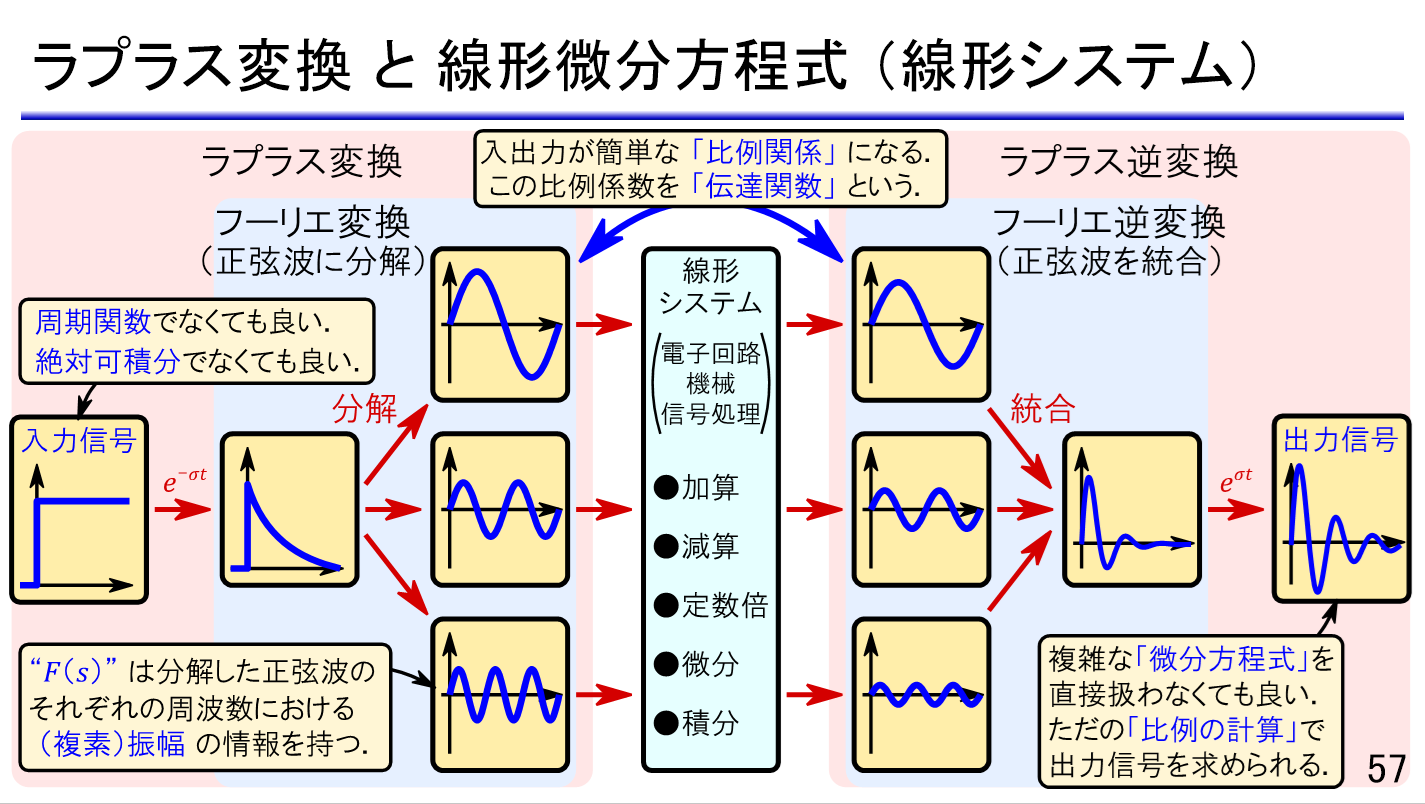
線形システムの導入
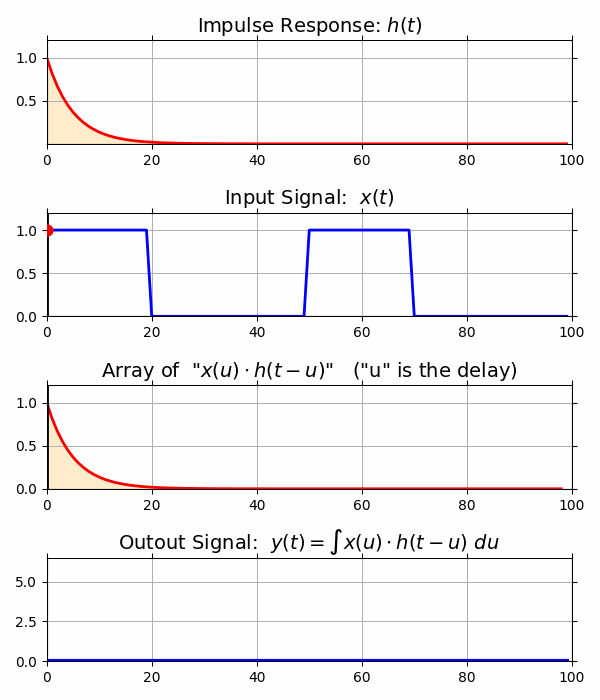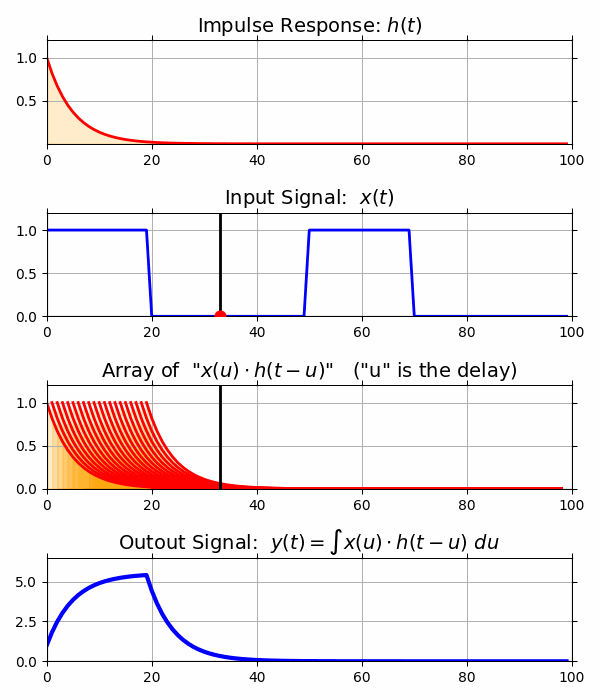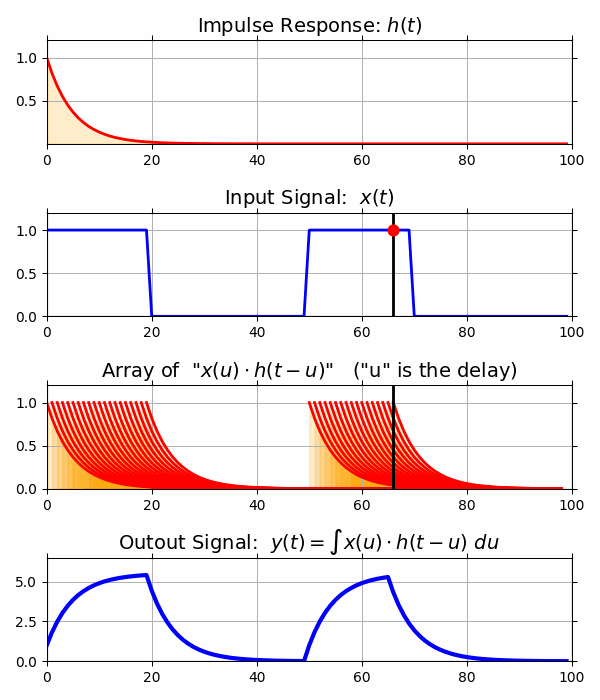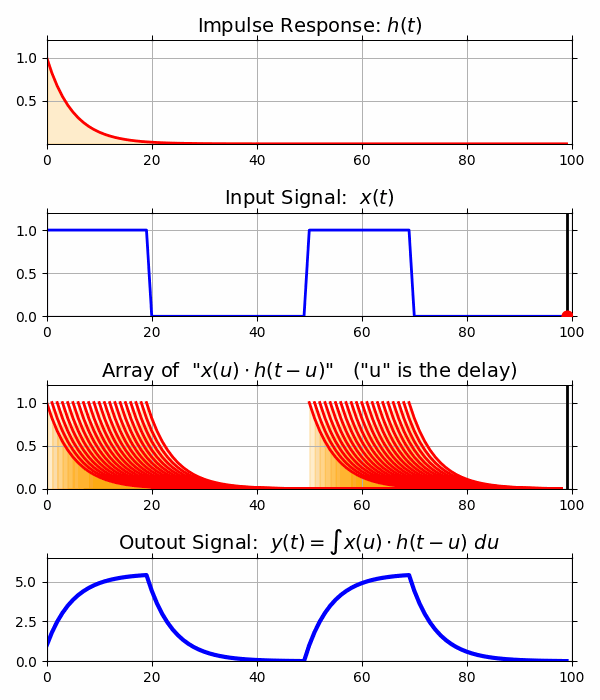
インパルス応答
伝達関数
インパルス応答を体感するアニメーションをPythonで作る


フーリエ変換とフーリエ逆変換をPythonで計算した様子	電気・電子工学の理論の地図

目標

あらゆるエンジニアリングの分野で活用されている「周波数解析」の本質を理解する
フーリエ級数，フーリエ変換，ラプラス変換とは何なのか説明できるようになる
線形システムにおけるインパルス応答や伝達関数の意味を理解する
線形システムと線形微分方程式の関係を理解する
回路設計やディジタル信号処理に必要な数学の基礎を身に着ける

対象

「フーリエ変換」や「ラプラス変換」，「伝達関数」，「インパルス応答」などを学びたい方
「周波数解析」の本質を理解して，分野を横断する見識を身に着けたい方
エンジニアとして「定量的な設計」をしたい方
これから電子回路設計，ディジタル信号処理，制御理論などを学びたい方

※「初等関数」および「微分・積分」はすでに理解しているものとします．詳しくは[講義ビデオ376分，講義テキスト222頁] Pythonで学ぶやりなおし数学塾1【微分・積分】をお求め・ご覧ください．

※本セミナではPythonの初歩的な文法は既知とした上で，学習の補助用にいくつかのプログラムを示します．Pythonの基礎は『実習キットでできる！ラズパイPicoでマイコン入門』などを参照してください．

※Python開発環境のインストール方法は，次の記事を参照してください．
　Pythonではじめる数値解析入門
　[Vol.1 Pythonの開発環境をインストールする]

準備するもの

簡単なクイズを出題するので，筆記用具と計算用紙があると便利です（任意です）．
あらかじめテキストを印刷しておくと便利です（2スライド/ページの両面印刷がおすすめですが任意です）．
自分のパソコンでPythonのプログラムを実行したい方は，あらかじめ実行環境（開発環境）をインストールしてください．なお，Pythonを知らなくてもフーリエ解析の内容は理解できます．

本オンデマンド製品を購入された方へ　～視聴リンクとパスワード～

下記リンク先(青字)をクリックして，本製品購入後にメールにてお知らせしたパスワードを入力してください．

338分講義ビデオ(著作権保護のためパスワードがかけられています)

20221030_Pythonで学ぶ_やりなおし数学塾2_フーリエ解析_Part1_zep.mp4

0:00:10 　イントロダクション
0:13:04 　「正弦波」が特別扱いされる理由
0:46:10 　関数の内積と三角関数の直交性
1:27:28 　実フーリエ級数（周期2π）
1:51:21 　実フーリエ級数（周期2T）

20221030_Pythonで学ぶ_やりなおし数学塾2_フーリエ解析_Part2_zep.mp4

0:00:10 　複素フーリエ級数
0:44:35 　フーリエ変換
1:05:24 　フーリエ変換の性質
1:41:25 　ラプラス変換
2:18:54 　デルタ関数の導入
2:47:00 　線形時不変システム

199頁講義テキスト(著作権保護のためパスワードがかけられています)

サンプル・ソースコード(著作権保護のためパスワードがかけられています)

program.zip

gifアニメーション(著作権保護のためパスワードがかけられています)

picture.zip

講師紹介

詳細はこちらを参照ください．

略歴

2011年　東京工業大学工学部　電気電子工学科　卒業
2013年　東京工業大学大学院理工学研究科　電子物理工学専攻　修了
2013年　株式会社アドバンテスト　入社
2016年　株式会社村田製作所　入社
2019年　リニア・テック　開業

主な著書

電子回路のキホン要点マスタ50，トランジスタ技術，2015年5月号，別冊付録，CQ出版社．
情熱のフル・ディスクリートFMラジオ，トランジスタ技術，2016年1月号　特集　第5章，CQ出版社．
本質理解！万能アナログ回路塾，トラジスタ技術，2017年9月号，連載，CQ出版社．
初等関数と微分・積分，2019年，CQ出版社．
月着陸船アポロに学ぶ確率統計コンピュータ，トランジスタ技術，2019年7月号　特集，CQ出版社．
大解剖！CPUはこうやって動いている，トランジスタ技術，2020年5月号　特集，CQ出版社．

プロの技術を1日で！
実習キット付き講義動画「スピードマスタ・シリーズ」

電子回路・基板設計からプログラミングまで，エンジニアがマスタすべき技術は多岐にわたり，開発期間も短くなっています．多くの書物を読み漁ったり，玉石混交のネット情報に振り回されたりしている暇はありません．

本シリーズには，各分野の一線で活躍する技術者が厳選したパーツセット，設計の要点を効率よく解説するセミナ動画，講義テキスト，お手本ソースコードなどが同梱されています．百戦錬磨の技を一見することで，未経験の技術が驚くほど短時間で身につくだけでなく，信頼性の高いシステム開発に必要なプロの眼が養われます．

［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】