Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】

LCRから高速伝送路/アンテナまで プログラミングで学ぶ電磁気学入門(講義790分/資料497頁)

• 著者・講師：別府 伸耕/Nobuyasu Beppu(リニア・テック)
• 企画編集・主催： ZEPエンジニアリング株式会社
• 1人当たり1ライセンスです


• 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
• 関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング 基礎編/応用編
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】


• 関連記事：Pythonではじめる 数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
• 関連記事：Pythonではじめる 数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]

お申し込み

ご購入

下記の購入するボタンを押して，必要事項の入力をお願いいたします．

ご購入前にご理解いただきたいこと

1. 本セミナは，2022年11月19日＆20日に開催したウェビナを録画して編集した動画です．繰り返し再生，一時停止，巻き戻しが可能です．

学ぶこと

電場編

あらまし

電子回路の基本素子である「インダクタ」や「キャパシタ」はもちろんのこと，高速信号用の「伝送線路」の設計や「半導体デバイス」を理解する上でも本質的な役割を果たす「マクスウェル方程式」を学ぶセミナの前半です．

「電場編」では，電磁気学全体を理解する上で不可欠な「ベクトル解析」を自由自在に使いこなせるようにします．「ベクトルの基礎」，「ナブラ」，「勾配」，「発散」，「回転」，「ガウスの発散定理」，「グリーンの定理」，「ストークスの定理」といった項目を丁寧に解説します．これらの数学的な道具が揃えば，マクスウェル方程式の中の1つである「電場に関するガウスの法則」を簡単に理解できます．さらに「保存場」や「電位」の概念を導入し，最終的に「キャパシタのI-V特性」を導きます．実際に電子回路を設計する際の注意点にも言及します．

演目

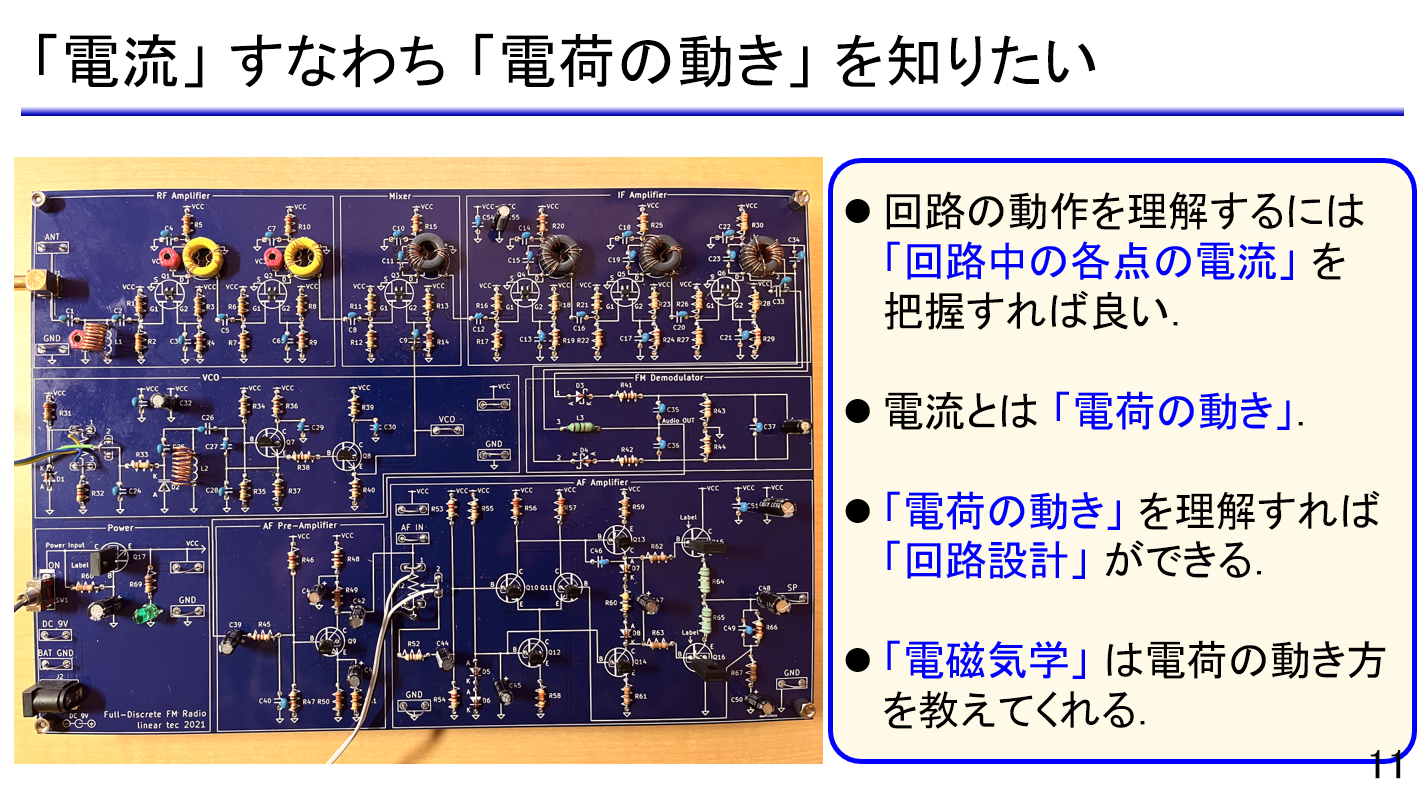
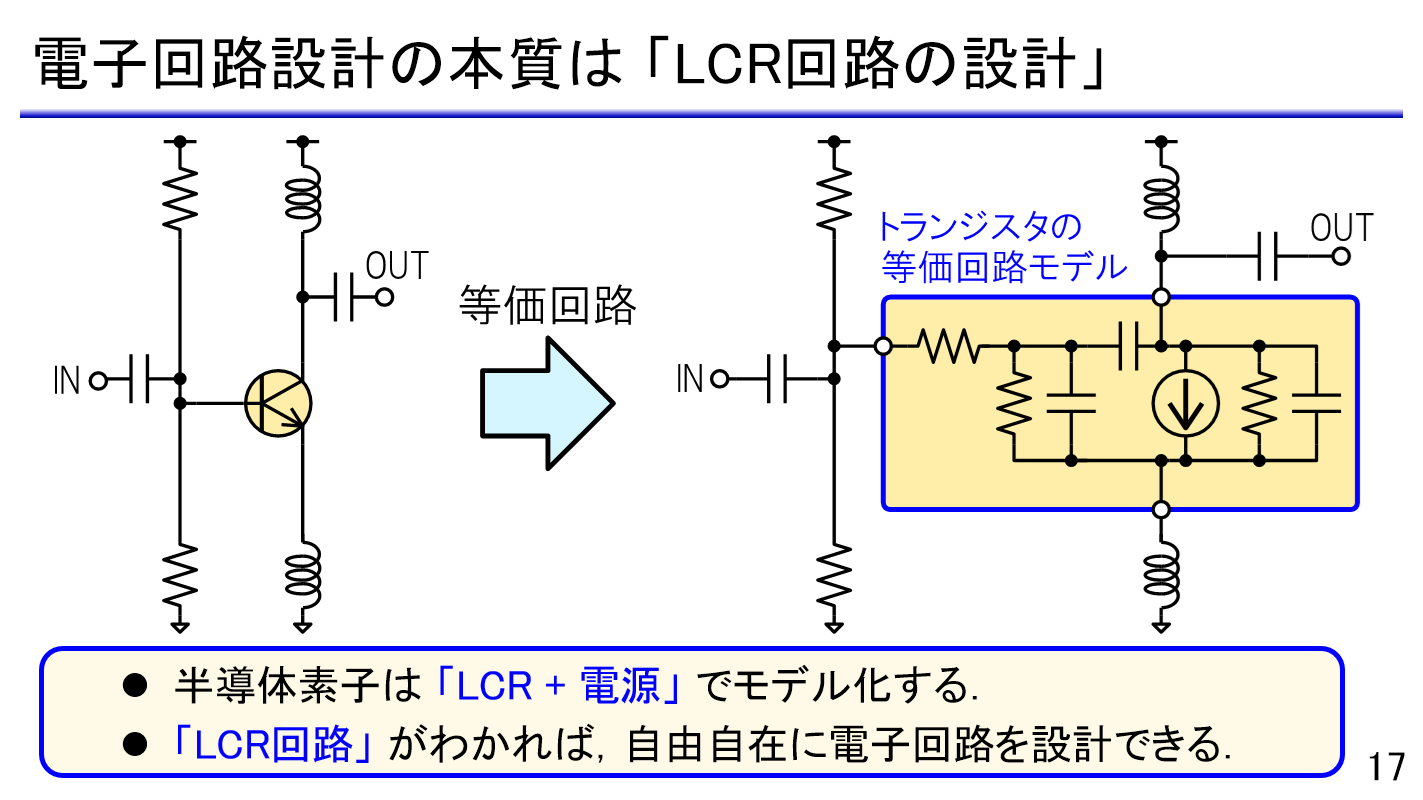
（1) 電磁気学と電気回路設計

• 回路設計の本質
• なぜ電磁気学が必要なのか
• 電気・電子工学の理論の地図
• 電磁気学の構造

（2）ベクトルとベクトル場

• ベクトルの基礎知識
• 内積と外積
• スカラ場とベクトル場

（3）クーロンの法則と電場

• クーロンの法則
• 電場の導入

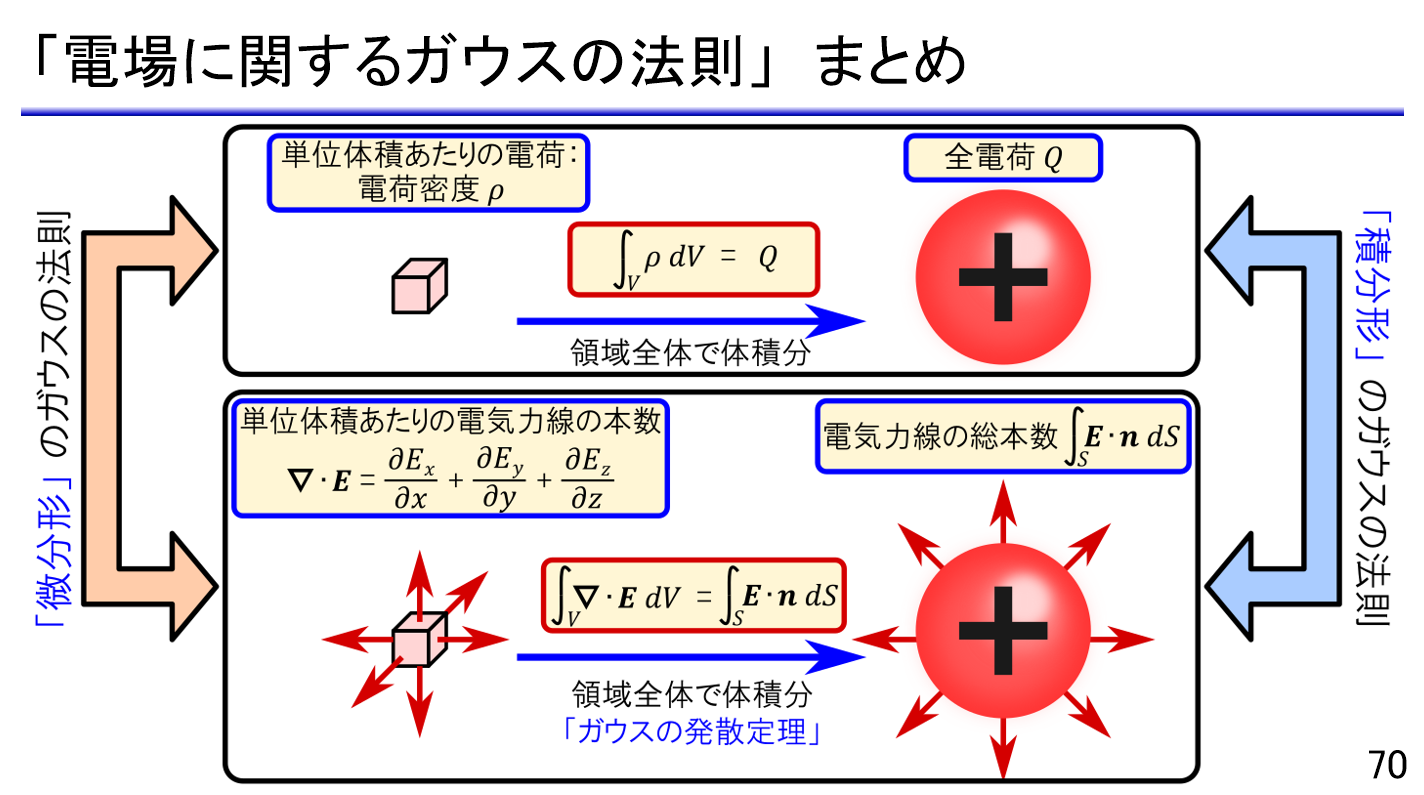
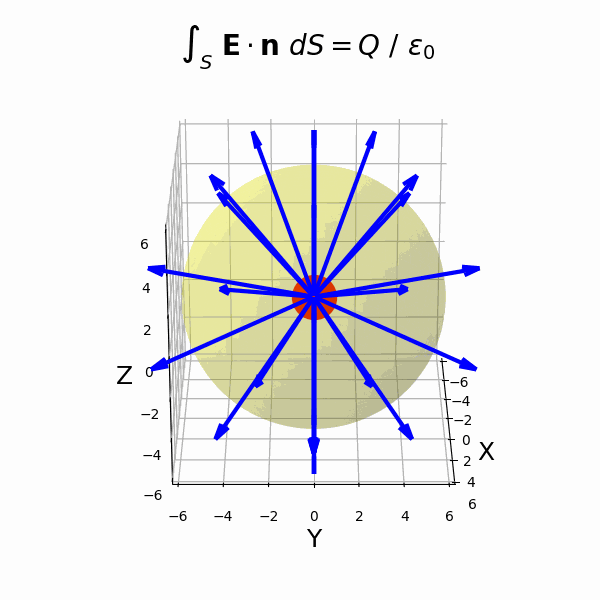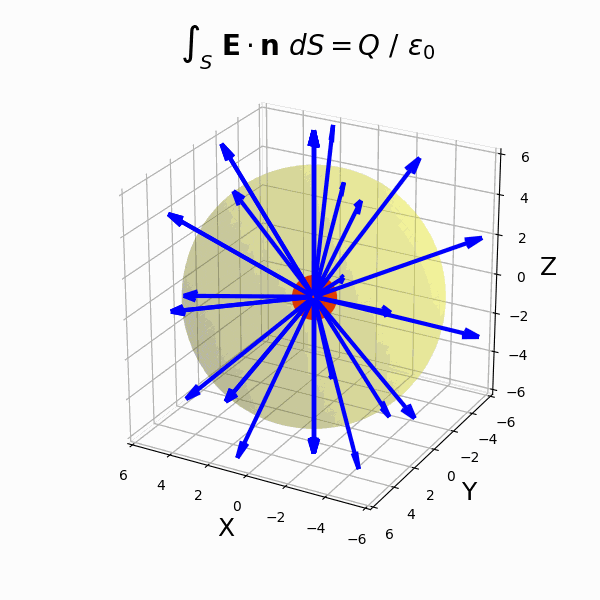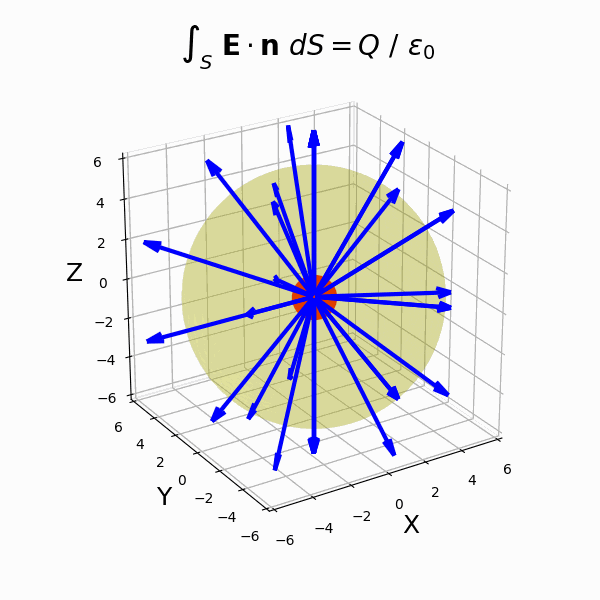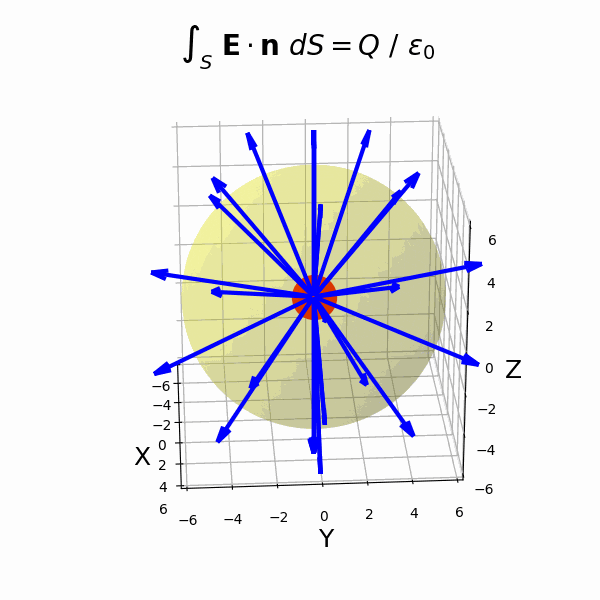
（4）電場に関するガウスの法則

• 積分形のガウスの法則
• 偏微分と全微分
• ナブラと勾配
• ベクトル場の発散
• ガウスの発散定理
• 微分形のガウスの法則

（5）電位とエネルギ

• 仕事とエネルギ
• 保存場
• ベクトル場の回転
• ストークスの定理
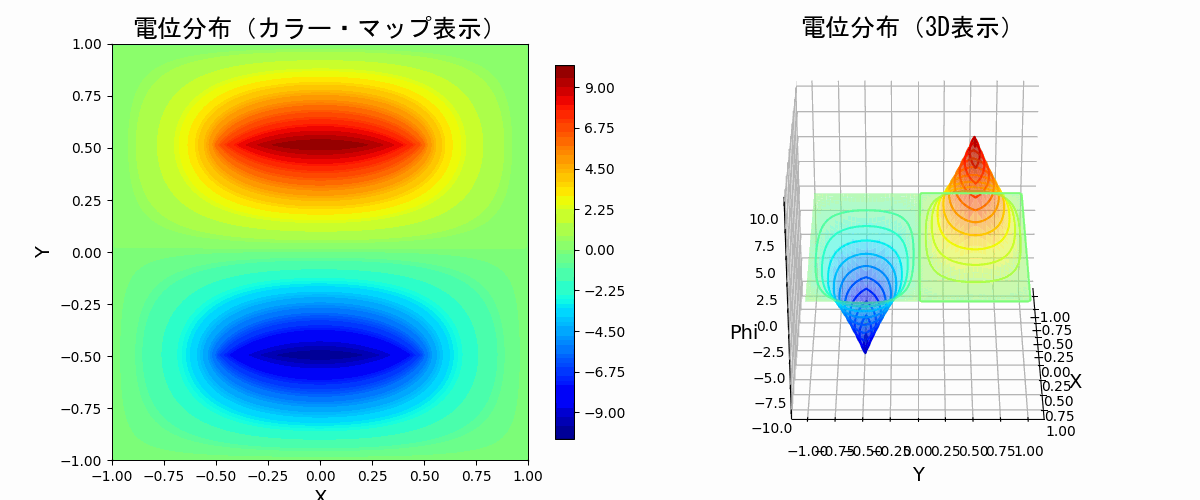
• 電位の導入

（6）ポアソン方程式

• ポアソン方程式の導出
• ポアソン方程式をPythonプログラムで解く

（7）導体

• 導体中の電場
• 静電遮蔽

（8）誘電体

• 誘電分極
• 誘電率
• 電束密度

（9）キャパシタ

• 静電容量
• キャパシタのI-V特性
• 実際のキャパシタ

磁場編

あらまし

電子回路の基本素子である「インダクタ」や「キャパシタ」はもちろんのこと，高速信号用の「伝送線路」の設計や「半導体デバイス」を理解する上でも本質的な役割を果たす「マクスウェル方程式」を学ぶセミナの後半です．

「磁場編」では，「電流にはたらく力」を中心として話を進めます．最初に「磁場」を導入し，「ビオ・サバールの法則」や「アンペールの法則」について解説します．その後「磁場に関するガウスの法則」，「アンペール・マクスウェルの法則」，「ファラデーの電磁誘導の法則」を導出します．前半の「電場編」と合わせると，これでマクスウェル方程式を構成する4つの方程式がすべて揃います．最後に「インダクタのI-V特性」を導き，電磁気学的な視点で回路設計を行う方法についてまとめます．

演目

（1）定常電流と回路

• オームの法則
• ジュールの法則
• キルヒホッフの法則

（2）電流にはたらく力と磁束密度

• 電流どうしにはたらく力
• 磁束密度の導入
• ローレンツ力
• ビオ・サバールの法則

（3）アンペールの法則

• 積分形のアンペールの法則
• 微分形のアンペールの法則

（4）ベクトル・ポテンシャル

• ベクトル・ポテンシャルの導入
• ベクトル・ポテンシャルとビオ・サバールの法則

（5）磁性体

• 分子電流と磁化
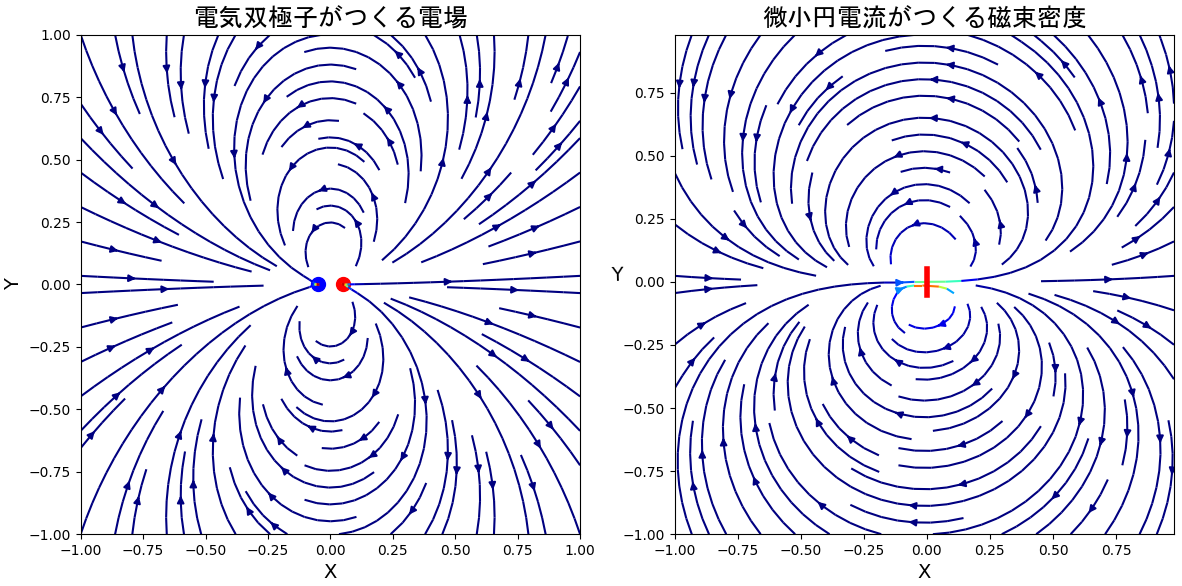
• 磁気双極子モーメント
• 常磁性，強磁性，反磁性
• 磁場の導入
• 透磁率

（6）アンペール・マクスウェルの法則

• 変位電流
• 積分形のアンペール・マクスウェルの法則
• 微分形のアンペール・マクスウェルの法則

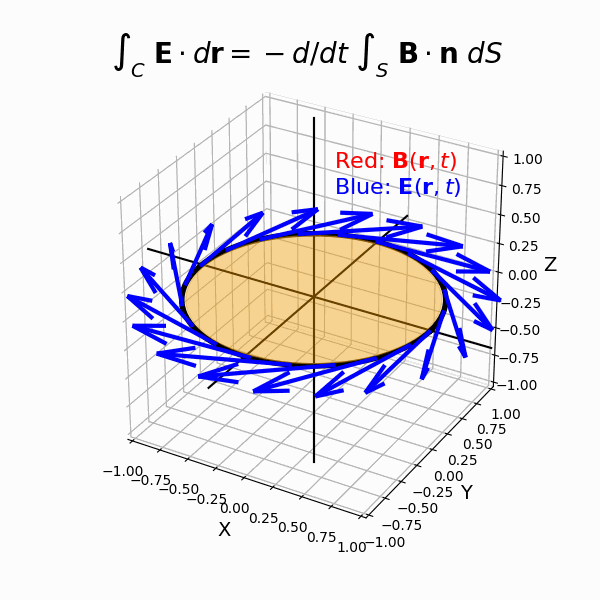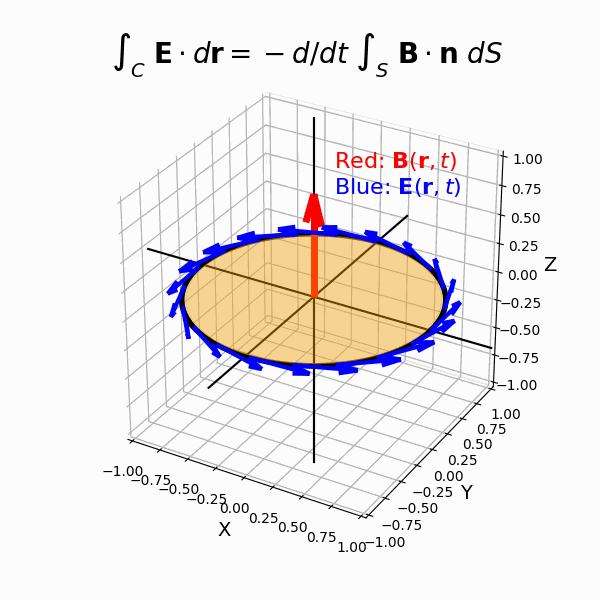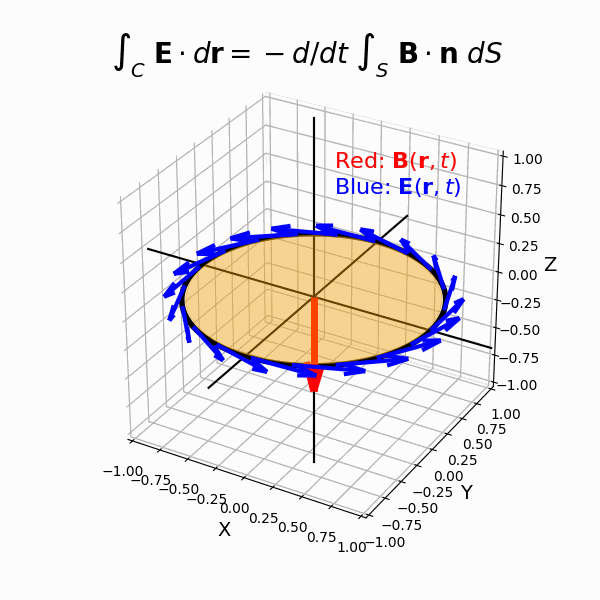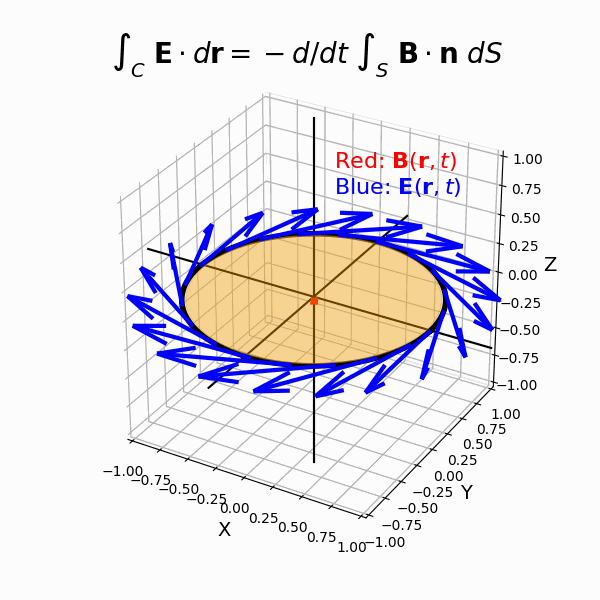
（7）ファラデーの電磁誘導の法則

• レンツの法則
• 積分形のファラデーの電磁誘導の法則
• 微分形のファラデーの電磁誘導の法則

（8）インダクタ

• インダクタンス
• インダクタのI-V特性
• 実際のインダクタ

講演の目標

• 「マクスウェル方程式」の本質を理解して回路設計に活かせるようになる
• インダクタ“L”，キャパシタ“C”，抵抗“R”を徹底的に理解する
• 電場“E”，電束密度“D”，磁束密度“B”，磁場“H”の役割を理解する
• 「勾配」，「発散」，「回転」といった微分演算を理解する
• 「ガウスの発散定理」や「ストークスの定理」といったベクトル解析の定理を理解する
• 真空の誘電率“ ^${ε_0}$ ”や真空の透磁率“ ^${μ_0}$ ”とは何なのか説明できるようになる

受講対象

• マクスウェル方程式を理解したい方
• 電磁気学で使う数学（ベクトル解析）を体系的に学びたい方
• キャパシタとインダクタの動作原理を理解したい方
• 低周波回路，高周波回路を問わず電気回路で起こる現象の本質を理解したい方
• 理論上の仮定（線形性）と現実の回路のひずみ（非線形性）を整理したい方
• 方程式で表される内容をPythonプログラムで表現したい方
• 初等関数（特に三角関数）と1変数の基本的な微分・積分は既に理解しているものとします．詳しい内容は『［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】』のセミナで解説します．
• 力学の初歩的な内容（運動方程式や仕事の定義など）は既に理解しているものとします

※本セミナではPythonの初歩的な文法は既知とした上で，学習の補助用にいくつかのプログラムを示します．Pythonの基礎は『実習キットでできる！ラズパイPicoでマイコン入門』のセミナで解説しています．

※Python開発環境のインストール方法は，次の記事を参照してください．
　Pythonではじめる 数値解析入門
　[Vol.1 Pythonの開発環境をインストールする]

受講者が準備するもの

• 簡単なクイズを出題するので，筆記用具と計算用紙があると便利です（任意です）．
• あらかじめテキストを印刷しておくと便利です（2スライド/ページの両面印刷がおすすめですが任意です）．
• 自分のパソコンでPythonのプログラムを実行したい方は，あらかじめ実行環境（開発環境）をインストールしてください．なお，Pythonを知らなくても微分・積分の内容は理解できます．

講師紹介

詳細はこちらを参照ください．

略歴

• 2011年　東京工業大学 工学部　電気電子工学科　卒業
• 2013年　東京工業大学大学院 理工学研究科　電子物理工学専攻　修了
• 2013年　株式会社アドバンテスト　入社
• 2016年　株式会社村田製作所　入社
• 2019年　リニア・テック　開業

主な著書

1. 電子回路のキホン 要点マスタ50，トランジスタ技術，2015年5月号，別冊付録，CQ出版社．
2. 情熱のフル・ディスクリートFMラジオ，トランジスタ技術，2016年1月号　特集　第5章，CQ出版社．
3. 本質理解！万能アナログ回路塾，トラジスタ技術，2017年9月号，連載，CQ出版社．
4. 初等関数と微分・積分，2019年，CQ出版社．
5. 月着陸船アポロに学ぶ確率統計コンピュータ，トランジスタ技術，2019年7月号　特集，CQ出版社．
6. 大解剖！CPUはこうやって動いている，トランジスタ技術，2020年5月号　特集，CQ出版社．