Pythonで一緒に！ロボット制御のモデルベース設計

安定余裕を確保して制御系をロバストにする


フィードバック制御系が安定でも油断してはいけない

いま，ロボット・アームの手先位置を目標の位置に追従させることを考えます．

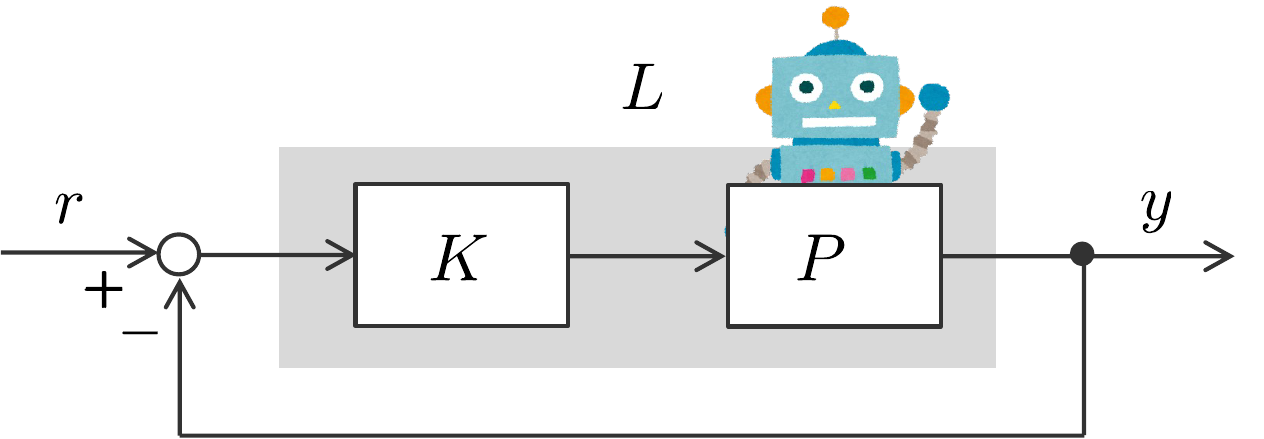
そのために，適当な制御則 $K$ を設計し，図1に示すようなフィードバック制御系を構築します．

図1　フィードバック制御系

ロボットアーム（制御対象）のモデルが

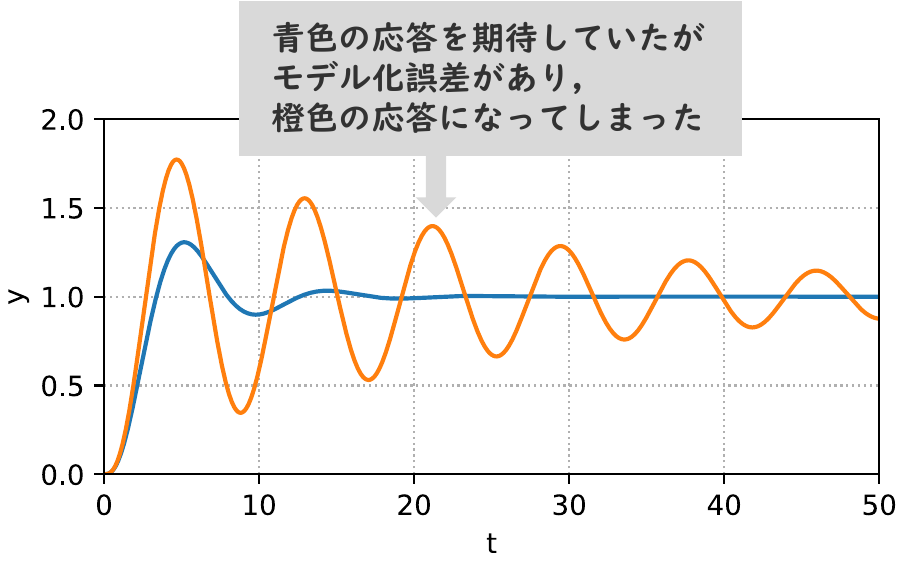
\begin{align} P(s) = \frac{1}{(s+1.2)^2} \end{align}

であるとき，これに対して，P制御 $K(s)=1$ を施します． このとき，ステップ目標値 $r(t)=1~(t\ge 0)$ を与えると，フィードバック制御系の出力 $y(t)$ は，図2の青線のようになります．

目標値の1の近くに収束していますので，フィードバック制御系は安定です．


図2　P制御系のステップ応答

さて，式（1）のモデルが正確ではなく，実際の制御対象が

\begin{align} P(s) = \frac{1}{(s+1.2)(s+0.6)} \end{align}

であったとしましょう．この場合，フィードバック制御系の応答は，図2の橙色の線に示すようになり，先ほどの青線の応答と比較すると振動的であることがわかります．式（1）と式（2）の違いはモデル化の誤差ですので，青線と橙色の応答の差は，モデル化誤差がフィードバック制御系に与える影響となります．

つまり，制御系を設計する際に用いた設計モデルが，制御対象そのものであれば，フィードバック制御系の応答が期待したとおりのものになりますが，設計モデルと制御対象にギャップがある場合には，期待したとおりの応答にならない可能性があるということです．最悪の場合，不安定になり，危険な状態になる可能性もあります．以下では，その例を示します．

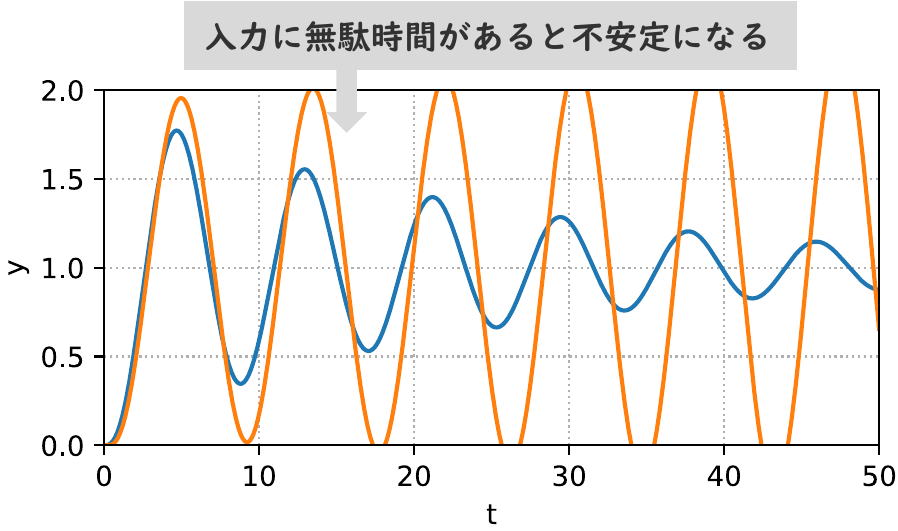
まず，入力に遅れ（無駄時間）がある場合です．0.2[s]の遅れがあるとき，実際の制御対象は，

\begin{align} P(s) = \frac{1}{(s+1.2)(s+0.6)}e^{-0.2 s}\simeq \frac{1}{(s+1)(s+0.6)}\cdot\frac{s-0.1s}{s+0.1s} \end{align}

となります（2つ目の式は，無駄時間要素を1次のパデ近似で近似したもの）． この場合，フィードバック制御系の応答は，図3の橙色の線となり，不安定になってしまいます．

図3　【例1】無駄時間がある場合の応答

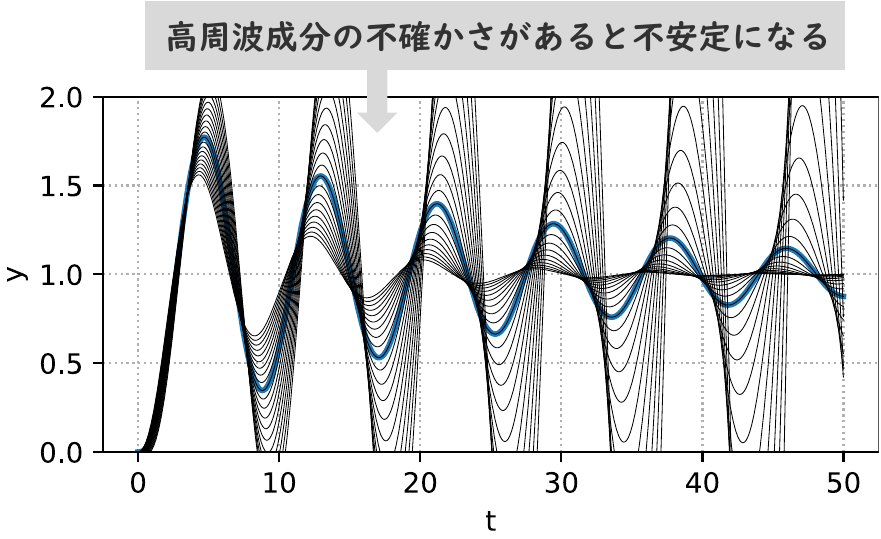
つぎに，無駄時間ではなくて，高周波特性にばらつき（不確かさ）がある場合，

\begin{align} P(s) = (1+\Delta(s)W(s))P_n(s),~~P_n(s) = \frac{1}{(s+1.2)(s+0.6)},~~ W(s) = \frac{50s}{s+150} \end{align}

を考えます（高周波域ではノイズの影響を受けやすく，そして特性を正確にモデル化することが難しい）．

ただし，$\Delta(s)W(s)$ は不確かさを表しており，$\Delta(s)$ は周波数ごとに 0 から 1 の値をとる伝達関数，$W(s)$は各周波数の不確かさの大きさを決める伝達関数です．このとき，図4の黒線のようになり，この場合もやはり不安定になります．

図4　【例２】高周波特性の不確かさがある場合

モデル化誤差がどれくらいなら許容できるのか

上記のように，制御系が安定であるからといって油断してはいけません．

モデル化誤差などがあっても，安定性を維持できる制御系を設計しておく必要があります．それを実現するための大事な指標が安定余裕（ゲイン余裕，位相余裕）です．

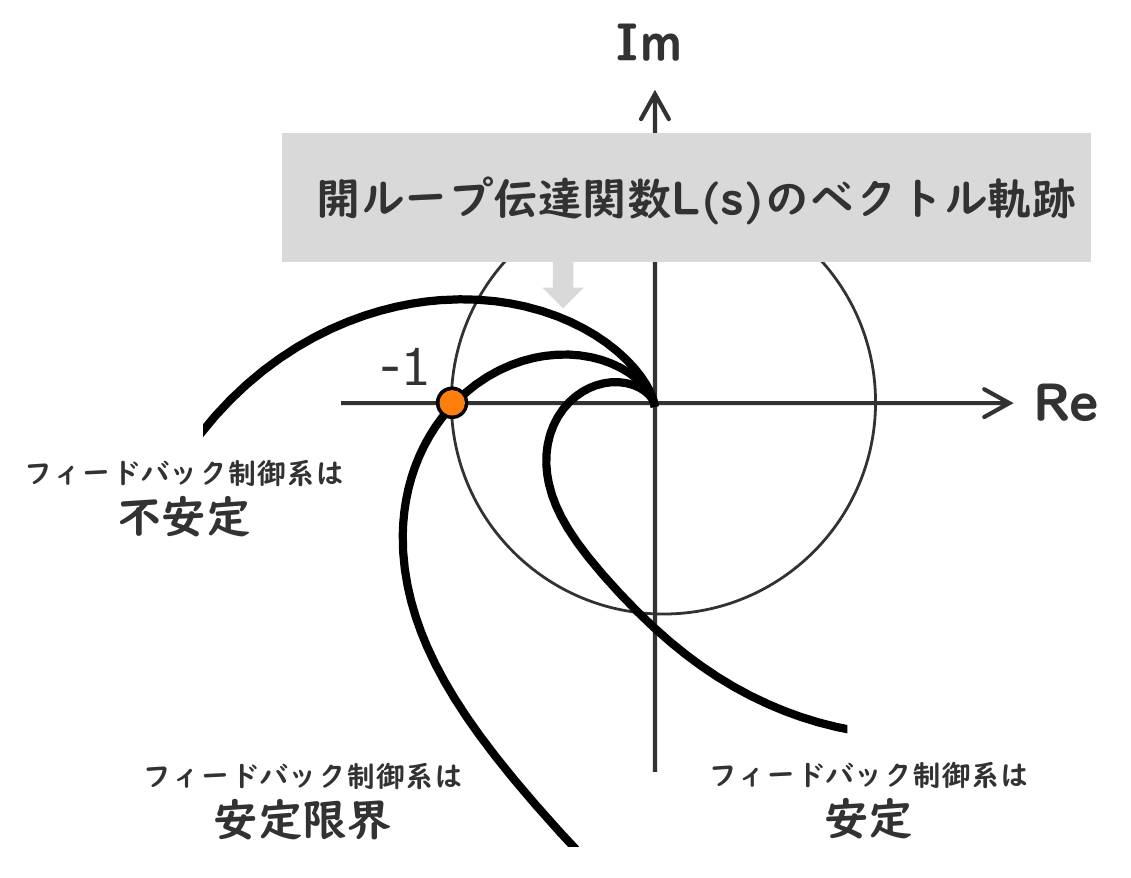
安定余裕は，開ループ系 $L(s) = P(s)K(s)$（図1の網掛け部分）の周波数領域における指標で，$L(s)$ のベクトル軌跡と$(-1, j0)$ の点との近さを評価するものです．

まず，開ループ系 $L(s)=P(s)K(s)$ の周波数特性の情報を利用して，フィードバック制御系の安定性を判別するナイキストの安定判別法を確認しておきます．

ナイキストの安定判別法によると，$L(s)$が安定な場合には，図5に示すように，$L(s)$のベクトル軌跡が，$(-1, j0)$ の点の右側を通ればフィードバック制御系が安定となり，左側を通ればフィードバック制御系が不安定となります．

図5　ナイキストの安定判別法（$L(s)$が安定）

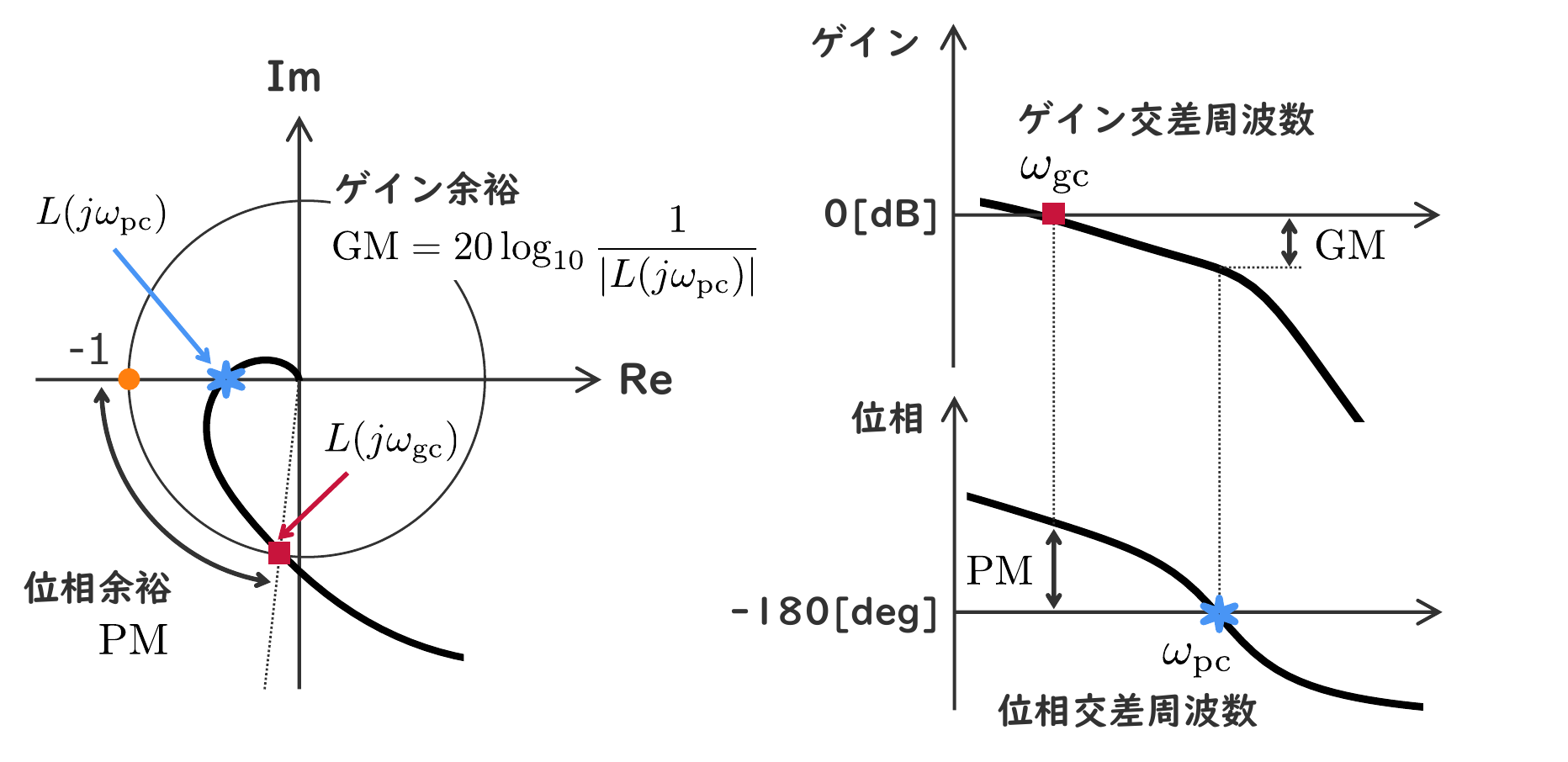
つぎは，図6を見てみましょう．

位相余裕 $\mathrm{PM}$ は，ゲイン交差周波数 $\omega_\mathrm{gc}$ における $L(s)$ の位相 $\angle L(j\omega_\mathrm{gc})$ が $-180\deg$からどれだけ進んでいるかを表すものです．式で書くと，

\begin{align} \mathrm{PM} = 180 + \angle L(j\omega_\mathrm{gc}) \end{align}

となります．ただし，ゲイン交差周波数$\omega_\mathrm{gc}$ は，$|L(j\omega)|=1$ となるときの周波数です．つまり，位相余裕は，$L(j\omega_\mathrm{gc})$ が$(-1, j0)$ の点からどれだけ離れているかを表しています．

そして，位相余裕が正であれば，フィードバック制御系が安定であり，さらに位相余裕が大きいほど制御対象のパラメータが変動しても不安定になりにくくなります．

図6　位相余裕とゲイン余裕

また，位相余裕に加えて，ゲイン余裕 $\mathrm{GM}$ という指標もあります．

ゲイン余裕 $\mathrm{GM}$ は，$|L(j\omega_\mathrm{pc})|$ の値をあと何倍すると 1 になるかを表すもので，デシベル表示では，

\begin{align} \mathrm{GM} = 20\log_{10} \frac{1} {|L(j\omega_\mathrm{pc})|} \end{align}

となります．ただし，$\omega_\mathrm{pc}$は，位相交差周波数で，$\angle L(j\omega) = -180\,\mathrm{deg} = -\pi\,\mathrm{rad}$ となるときの周波数です．つまり，ゲイン余裕 $\mathrm{GM}$ は，位相交差周波数 $\omega_\mathrm{pc}$ における $L(j\omega_\mathrm{pc})$ が$(-1, j0)$ の点からどれだけ離れているかを表しています．

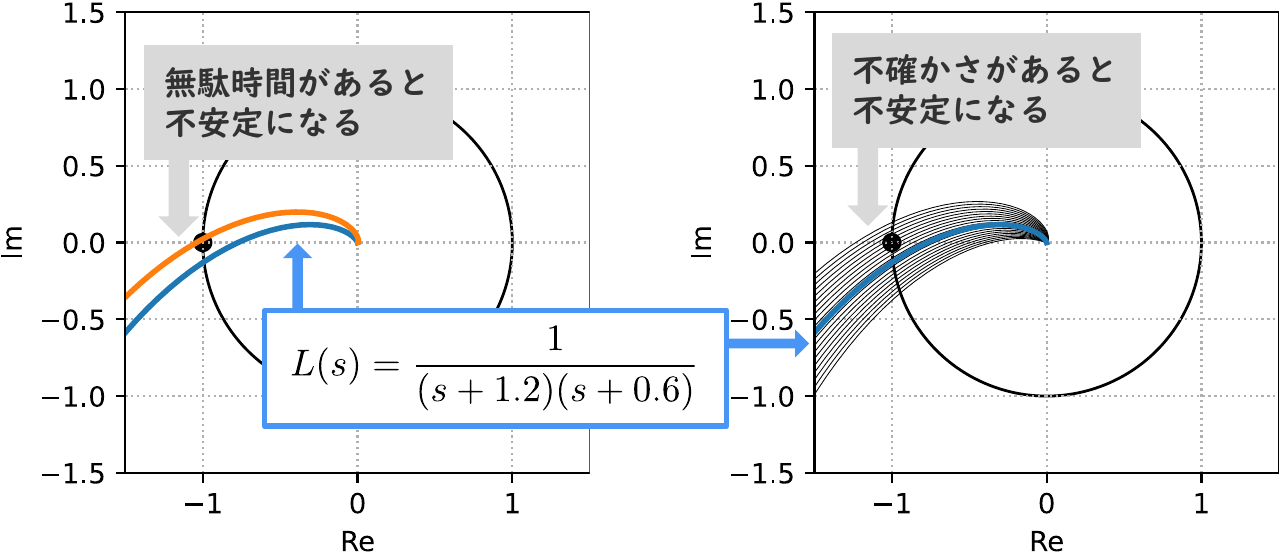
上記を踏まえて，前節の無駄時間がある場合（例1）や高周波特性に不確かさがある場合（例２）における開ループ伝達関数 $L(s)$ の特性を確認しましょう．$L(s)$のベクトル軌跡を図7に示します．制御則がP制御 $K(s)=1$ であることに注意してください．

左図において，無駄時間がない場合が青色の線，ある場合が橙色の線です．これより，無駄時間が加わることで，$L(s)$のベクトル軌跡が$(-1, j0)$ の点の左側をとおり，フィードバック制御系が不安定になることがわかります．同様に，右図の黒線で示すように，不確かさがある場合にも，$L(s)$のベクトル軌跡が$(-1, j0)$ の点の左側をとおり，フィードバック制御系が不安定になることがわかります．

位相余裕が小さいために，このようなことになります．

図7　【例1】と【例２】の開ループ系のベクトル軌跡

位相余裕を考慮してロバストにする

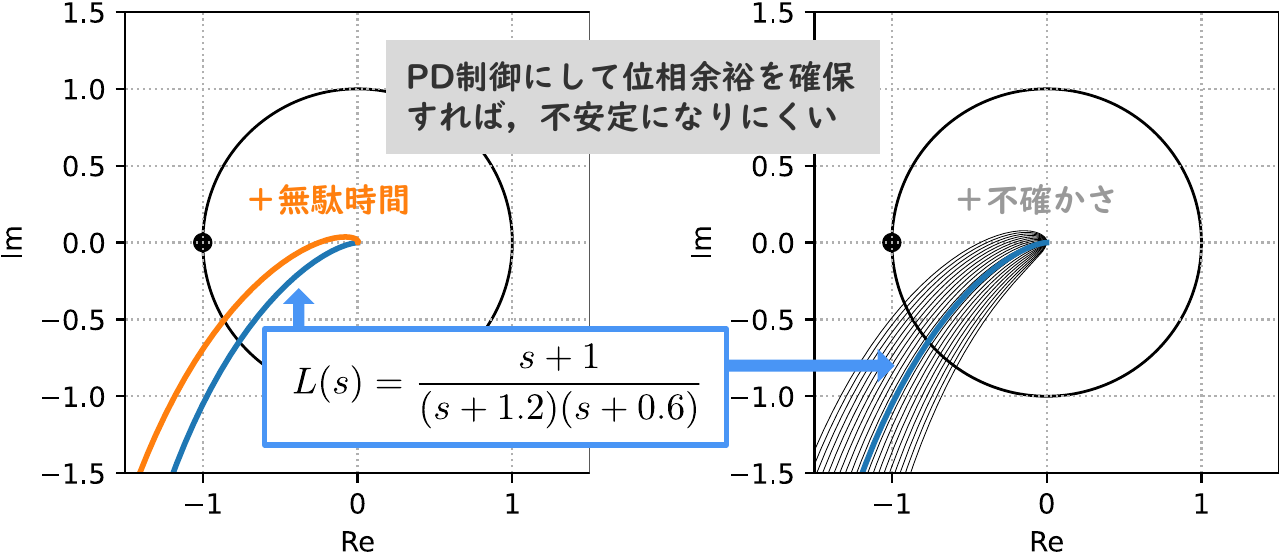
位相余裕を確保するために，制御則をPD制御 $K(s) = 1+s$ に変更してみます．微分は位相を進ませますので，これにより，位相余裕が大きくなります．

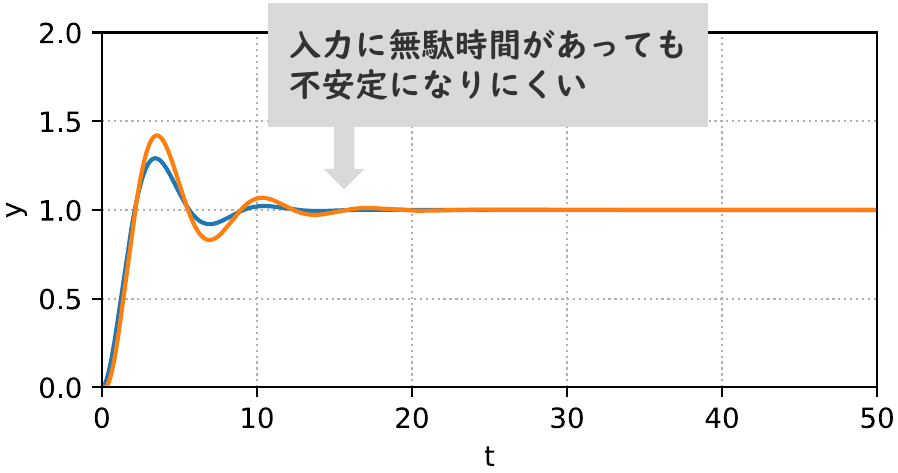
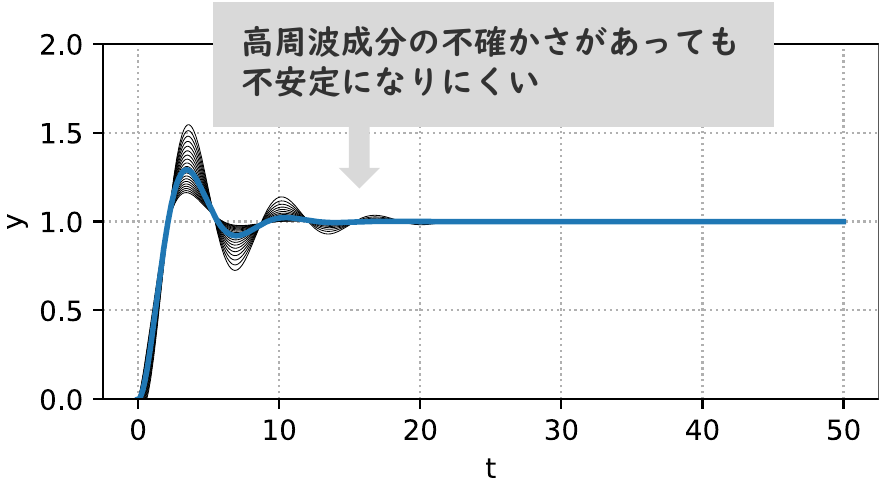
実際，開ループ伝達関数 $L(s)$ のベクトル軌跡を描くと，図8のようになります． 無駄時間や高周波特性の不確かさがあっても，ベクトル軌跡は，$(-1, j0)$ の点の右側を通ることがわかります．

図8　PD制御の場合の開ループ系のベクトル軌跡

さらに，フィードバック制御系のステップ応答を図9と図10に示します．

P制御の場合（図3と図4）と比較すると，無駄時間や不確かさに対してロバストな制御系になっていることがわかります．

なお，図の青線の応答を比べてみると，そもそも，振動が抑えられていることがわかります．つまり，位相余裕が大きくなるように制御系を設計することで，振動を抑制できます．

図9　PD制御系のステップ応答（無駄時間がある場合）
図10　PD制御系のステップ応答（高周波特性に不確かさがある場合）

一般に，正確なモデル化は難しいため，モデル化誤差は避けられません．また，正確なモデルが構築できる技術があったとしても，制御系設計の見通しをよくするという観点から，簡易モデルを構築することもあります．そういった場合には，今回の位相余裕を考慮した設計をはじめとしたロバスト制御系設計が役に立ちます．〈南 裕樹〉