LTspice設計データで学ぶ Analog Devices電子回路教室

一緒に定番シミュレータLTspiceを動かしながら学ぶ

• 著者・講師：石井 聡 / Satoru Ishii（アナログ・デバイセズ株式会社 プリンシパル・エンジニア）
• 企画・編集：ZEPエンジニアリング株式会社
• 提供：DigiKey

● 連載目次（全4回）

　　　第1回　OPアンプの周波数特性と適切な選び方
　　　第2回　高精度増幅を実現するOPアンプの選び方
　　　第3回　低電圧/単電源動作のための適切なOPアンプ選定
　　　第4回　安定に動作する負帰還アンプの検証と構築

第4回　安定に動作する負帰還アンプの検証と構築

1. はじめに
2. OPアンプ内部回路と位相遅れ
3. OPアンプ出力に容量が接続されると
4. 安定性の評価方法と位相余裕
5. 安定性なOPアンプ増幅回路を安定化させる方法
6. 位相余裕の理論的意味あいと確認方法

パソコンで電子回路を動かしてみよう

下記から，著者の石井 聡氏が設計したLTspice（アナログ・デバイセズ製）用の回路ファイルを無償でダウンロードできます．電子回路シミュレータLTspiceをパソコンにインストールすれば，著者と同じ実験・測定用のバーチャル環境を構築でき，プロの設計技術をそのまま体験しながら学習できます．

1. 連載第1回～第4回のLTspice回路ファイルをダウンロードする
2. 電子回路シミュレータLTspiceをダウンロードする

1．はじめに

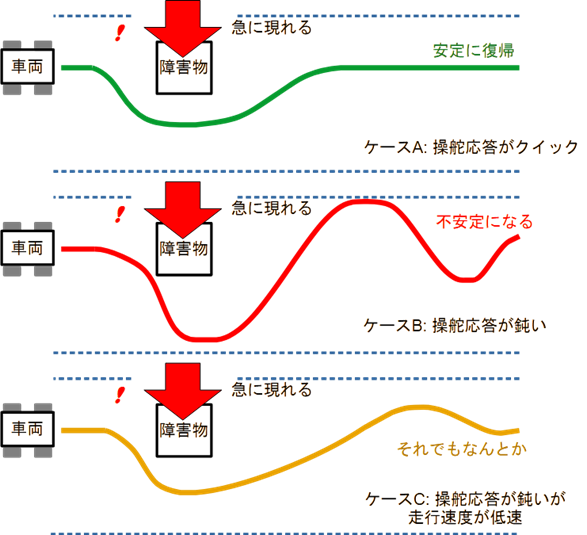
今回（最終回）はOPアンプの安定性について解説します．「安定性とは？」とその意味合いについて戸惑うと思いますので，最初にその意味を説明します．図1のような道路を走る自動車の例を考えてみましょう．このような例示によるイメージがOPアンプの安定性の意味を理解するにはよいと思います．

さて，自動車は「走る・曲がる・止まる」の性能が基本と言われています．とくに「走る・曲がる」においては，ハンドルのレスポンス（操舵応答）が大きく性能に影響を与えます．一番上の例は，操舵応答がクイックな車両の例です．急に目の前に障害物が現れてもハンドル操作にクイックに車両が応答するので，すぐに元の経路に安定に復帰できます．

真ん中の例は，操舵応答が鈍い（遅延がある）車両の例です．急に目の前に障害物が現れると，車両の応答が遅れ，なおかつもとに戻そうと思っても大きく左右に振れてしまい，なかなか元の経路に戻れませんし，非常に危険です．最悪，壁面に衝突したりスピンしたりしてしまうこともあるでしょう．

図1の例は，操舵応答が鈍い（遅延がある）車両ですが，走行速度が遅い例です．操舵応答が鈍くても障害物をよけることはでき，少し左右に振れても何とか元の経路に戻ることはできます．

OPアンプ増幅回路もまったく同じなのです．その周波数特性が許す限り，抵抗で設定された動作ゲインで，OPアンプの出力は入力信号に対して余計な「暴れ」なく追従しなくてはなりません．この記事では，負帰還動作をより詳しく掘り下げ，不安定になるしくみと回路を安定化させる考え方，そして安定・不安定の指標について説明します．

2．OPアンプ内部回路と位相遅れ

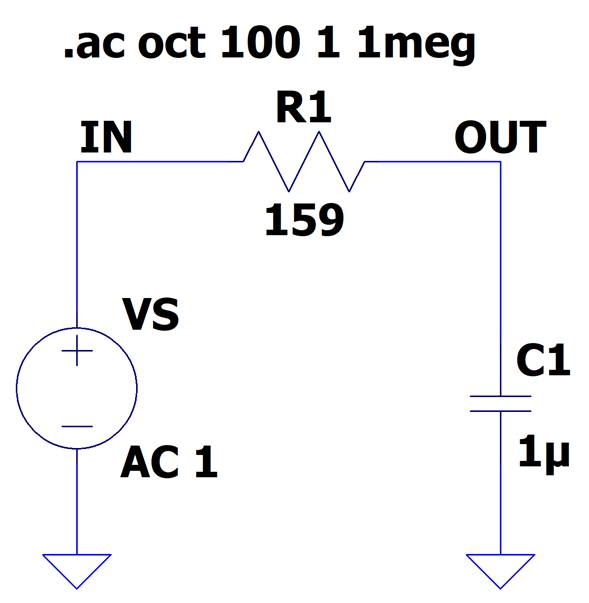
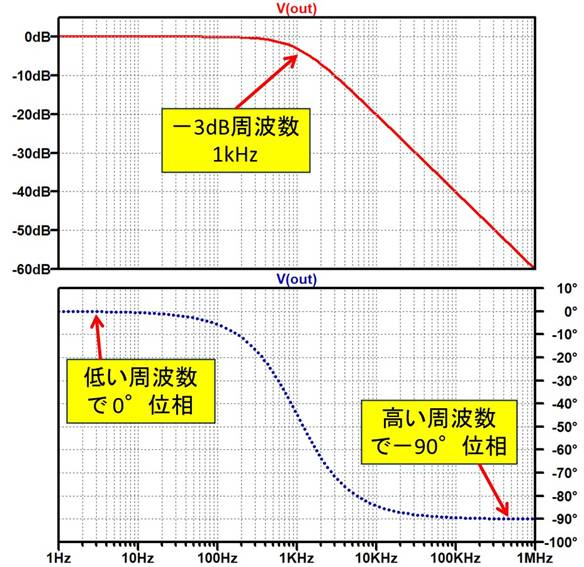
図2は抵抗とキャパシタ（$RC$）で形成された，$-$3dB周波数が1kHzとなる$RC$ローパス・フィルタです．図3にこの入出力特性を示します．

この図では，上が振幅特性，下が位相特性になっています．低い周波数では入出力の位相は0°ですが，周波数が高くなると$-$90°になります．「位相が$-$90°」というのは，入出力で波形のタイミングが1/4周期遅れることを意味します．これは自動車であれば，操舵の応答が遅れるイメージです．

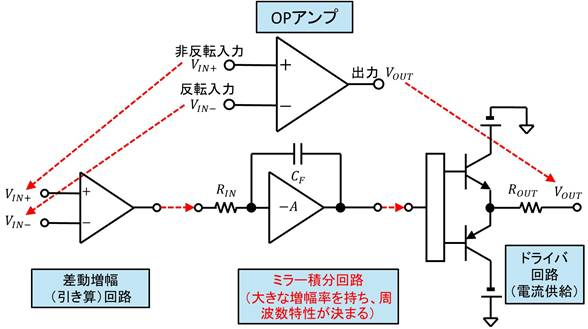
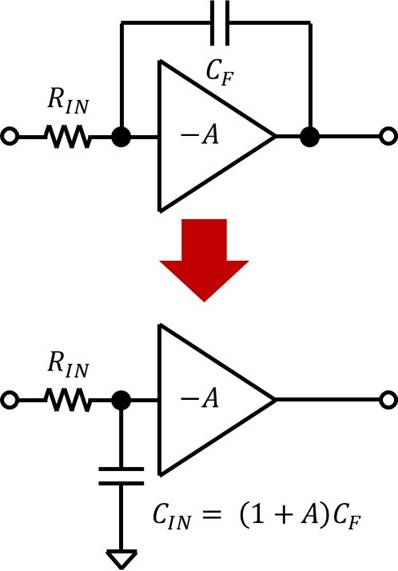
続いて図4にOPアンプの非常に基礎的な内部構造を示します．OPアンプは入力の差動増幅回路，大きなゲインと周波数特性を決める要素であるミラー積分回路，ドライバ回路から構成されています．このうちミラー積分回路は，抵抗$R_{IN}$とキャパシタ$C_F$と反転増幅回路から成り立っています．

図中の$C_F$は，反転増幅アンプ部分のゲインを$-A$とすると，図5のように入力にシャントされる入力容量$C_{IN}$として等価的に置き換えられ，$C_F$が1$+A$倍に見えます．つまりこの回路の効果として，小さい容量でも非常に大きな（見かけ上の）入力容量$C_{IN}$を構成できます（たとえば$C_F$ = 1pF，$A=$1,000,000なら$C_{IN}$ = 1$\mu$F）．

ここに$R_{IN}$が159k$\Omega$であれば，$-$3dB周波数が1Hzの$RC$ローパス・フィルタがOPアンプ内部に構成されることになります．これは図3において直流ゲインが120dB，中央が1Hzになるものに相当し，またこれが第1回で示したOPアンプのオープン・ループ・ゲインの周波数特性を決めるものになります．OPアンプの安定性という観点では「OPアンプは周波数が上昇すると，位相が$-$90°になる」ということがポイントです．

これは図2でも示したように，入出力で波形のタイミングが1/4周期遅れることを意味します．繰り返しますが自動車であれば，操舵の応答が遅れるイメージです．

3．OPアンプ出力に容量が接続されると

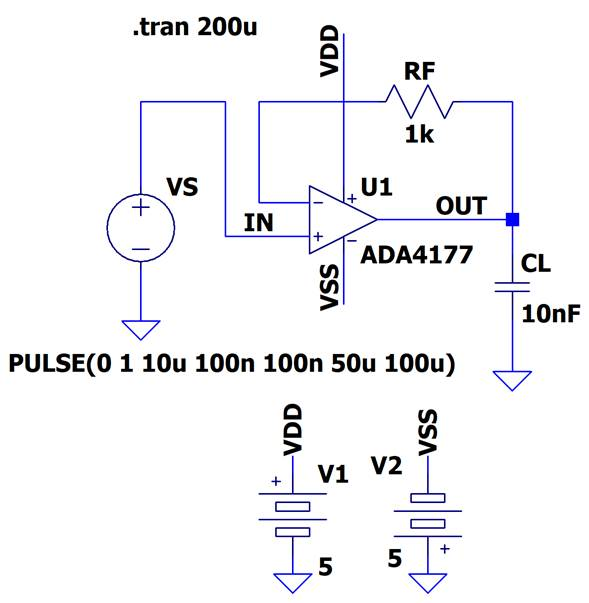
図6のように，OPアンプ出力に容量$C_L=$10nF（0.01$\mu$F）が接続されたことを考えてみます．ここで使用しているOPアンプはADA4177-2というものです．

図4にも記載してあるように，OPアンプ出力のドライバ回路も出力抵抗$R_{OUT}$はゼロではなく，数10$\Omega$から数k$\Omega$の抵抗値があります．帰還回路としてOPアンプを動作させている場合は，この抵抗は，帰還動作により1/（1 +$ A \beta）$倍に低減されて「見かけ上は」かなり低くはなりますが，容量$C_L$にとっては，$R_{OUT}$が直接見えることになります．

ADA4177-2のデータシートには数値の記述がありませんが，ADA4177-2の出力抵抗$R_{OUT}$を500$\Omega$と仮定すれば，$R_{OUT}$と$C_L$とで$-$3dB周波数が31.8kHzとなる$RC$ローパス・フィルタが形成されます．31.8kHzではOPアンプ内部のミラー積分回路による$RC$ローパス・フィルタでの位相遅れは$-$90°になっていますし，この$-$3dB周波数31.8kHzの10倍の周波数（318kHz）で$R_{OUT}$と$C_L$による位相遅れもほぼ$-$90°になりますから，318kHzより上の周波数においては，ADA4177-2の入力端子INからOUTにかけてトータルで$-$180°の位相遅れが形成されることになります．

本来，OPアンプの反転入力には，加えた信号と同位相の電圧が帰還されるべきです．これが反転入力により引き算され，過度な増幅動作を抑え込む・安定化させる「負帰還動作」が実現されています．

しかしこの説明のように，位相が$-$180°遅れてしまえば，負帰還とはならず「正帰還動作」になります．位相が完全に$-$180°遅れれば異常発振が生じますし，そこまでいかなくとも，$-$180°に近づいていくと回路動作が不安定になります．まさしく操舵性の鈍い自動車のはなしとまったく同じになります．

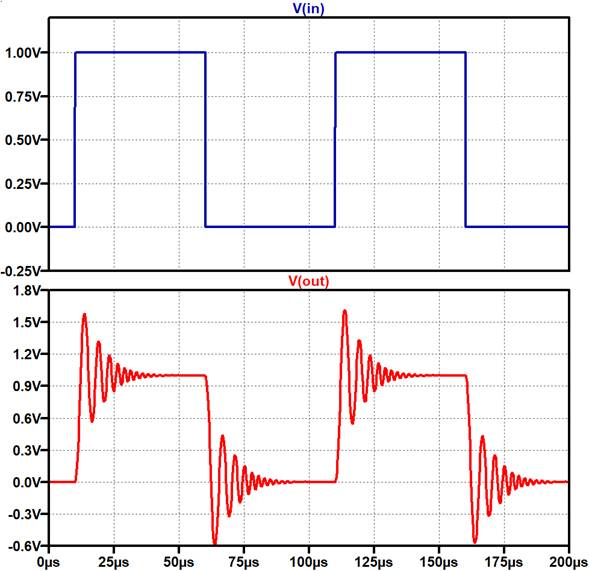
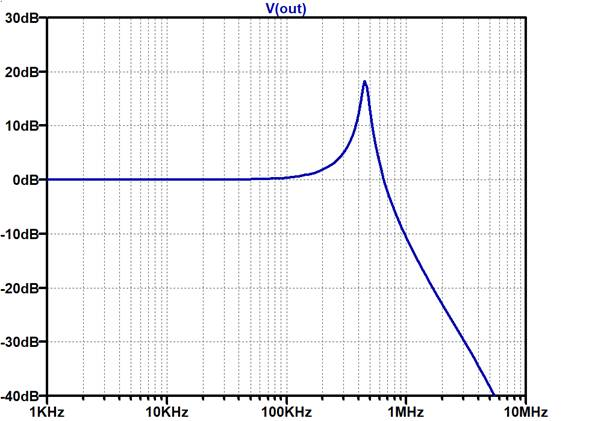
図7に矩形波入力への応答（図6のシミュレーション結果）を示します．また図8にAC解析による周波数特性を示します．

図7では非常に大きな暴れ（リンギング．ここでは150$\%$程度），図8では周波数が低下し始めるべきあたりで大きなピーク（ピーキング．ここでは+18dB程度）が生じていることがわかります．

このように，OPアンプは容量性負荷に対して弱い点に注意が必要です．またOPアンプ出力に同軸ケーブルを直結した場合も，同軸ケーブルは1mあたり100pFの容量がありますので，容量負荷相当となり同じ挙動になります．容量負荷以外にも，帰還抵抗とOPアンプの入力容量との間でもまったく同じしくみで位相遅れが生じ，不安定になることがあります（連載 第1回「7．周波数特性はいつでもなだらかに低下するとはいえない」で示した）．

4．安定性の評価方法と位相余裕

OPアンプ増幅回路が安定になっているかは，図7や図8でみてきたような矩形波応答や周波数特性で確認できます．これはシミュレーション，実測のどちらでも応用可能です．この評価指標として，以降に詳しく説明する「位相余裕」というものがあります．

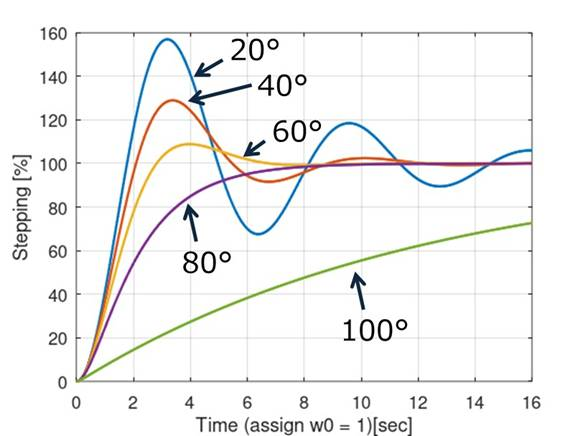
図9は矩形波応答と位相余裕の関係です．

回路に矩形波を加えて出力の応答を時間軸で確認します．位相余裕により応答の形状が異なっていますが，リンギングが大きいほど回路が不安定です．図7の例は不安定な（位相余裕が少ない）ことがわかります．一般的には位相余裕を40° ～60°くらいにして，収束がよい（安定で高速）状態を形成します．なお矩形波応答による確認ですので，OPアンプのスルーレート制限に注意して実施してください．

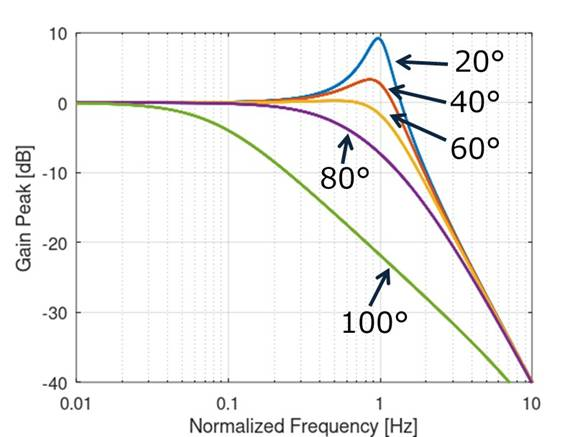
図10は周波数特性と位相余裕の関係です．回路入出力の周波数特性を周波数軸で確認します．周波数上昇でゲインが低減していく形状が位相余裕により異なっていますが，ゲイン・ピークが大きいほど回路が不安定です．図8の例は不安定な（位相余裕が少ない）ことがわかります．ここでも位相余裕を40° ～ 60°くらいにすると周波数特性がなだらかに変化し，安定で高速な状態になります．

5．OPアンプ増幅回路を安定化させる方法

上記のように，シミュレーションや実測で安定性の評価をおこない，問題がなければよいのですが，位相余裕が少ない場合は，以下の方法で安定化を確保できます．これら以外にも方法はありますが，ここでは3つの方法を例として示します．それでもどの方法も万能ではなく，いくぶん厄介だともいえます．

5.1　進み位相補償を施す

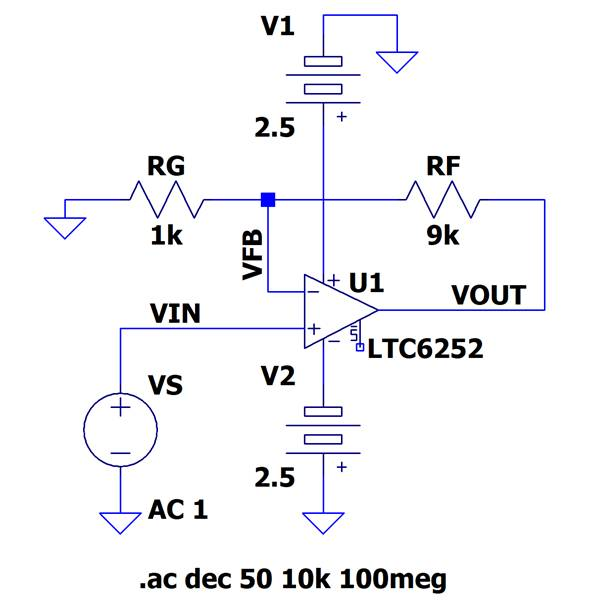
図11は，$GB$積720MHzの高速OPアンプ LTC6252を$G=$20dBで構成したものです．

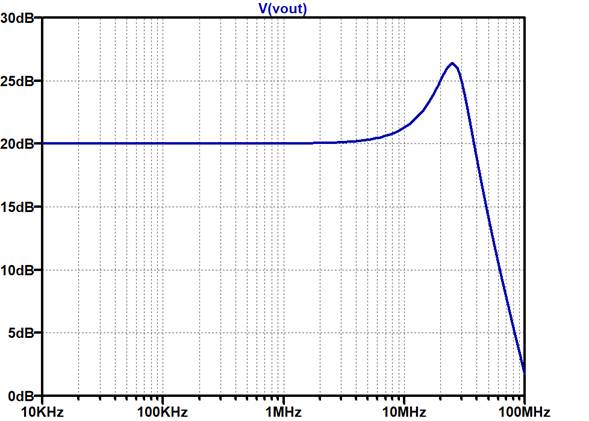
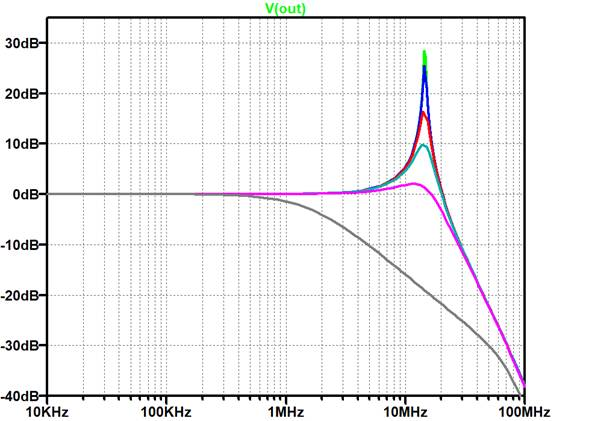
帰還抵抗$R_F$，$R_G$を適切な大きさから少し大きめにしており，帰還抵抗と入力容量（2.5pF）で位相遅れが生じる構成にしてあります．図12はこの回路の周波数特性をシミュレーションしたものです．ゲインのピークが7dB程度あり，位相余裕が30°程度と想定され，少し不安定ぎみです．

続いて図13に，図11の帰還抵抗$R_F$に並列に容量1pFを接続したときの周波数特性を示します．上のプロットのようにピーキングが消えています．ここに容量を接続することにより，同図下のプロットのようにOPアンプ出力から非反転入力にかけての帰還回路の位相が特定の周波数で進むことになり，位相特性を改善できます．容量負荷が接続された場合も同様に応用できます．これを「進み位相補償」と呼びます．

この補償方法は動作ゲインが低いとき，つまり$R_F$と$R_G$の値の比が小さいとき効果は低くなります．ある程度の動作ゲインがある回路での対策と考えてください．

5.2　容量負荷を分離する

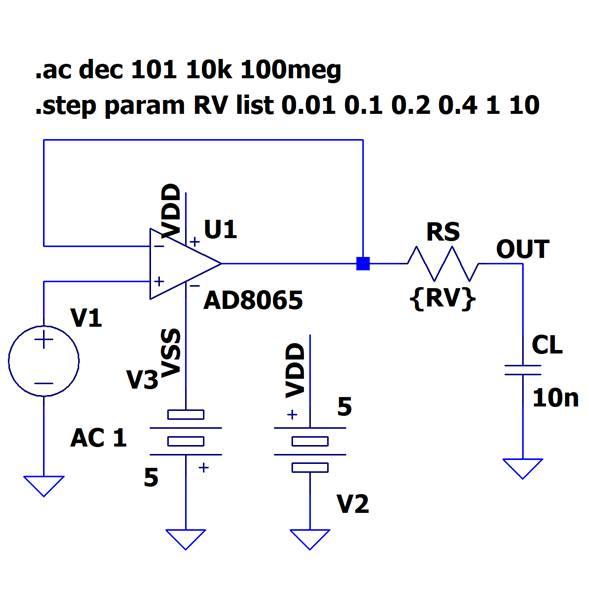
図14はFET入力高速OPアンプAD8065出力に容量$C_L$ = 10nF（0.01$\mu$F）が接続された回路です．

この回路はボルテージ・フォロアのため，先に説明した容量による進み位相補償は適用できません．そこで回路図のようにOPアンプ出力と容量負荷の間に抵抗$R_S$を挿入して，負荷容量を分離するという方法を取ります．

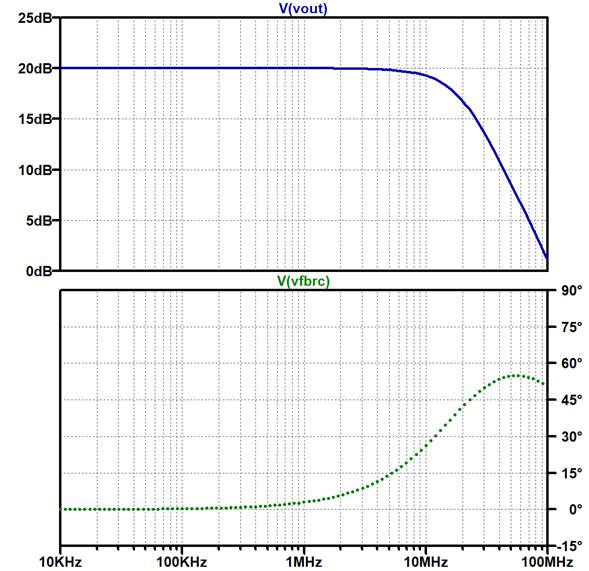
シミュレーションでは抵抗値$R_S$を10m$\Omega$，0.1$\Omega$，0.2$\Omega$，0.4$\Omega$，1$\Omega$，10$\Omega$に変化させてその周波数特性を確認してみます．シミュレーション結果を図15に示しますが，$R_S$ =1$\Omega$で十分なことがわかります．

このように小さい分離抵抗で十分な場合が多いといえます．デメリットは，$R_S$，$C_L$でできる$RC$ローパス・フィルタによる高域での出力レベルの低下，また重い（低い抵抗値の）負荷抵抗が接続された場合に$R_S$とで分圧されることによる高出力での出力レベルの低下があります．それぞれLTspiceでシミュレーションにより確認できます．

5.3　より高度な二重帰還補償

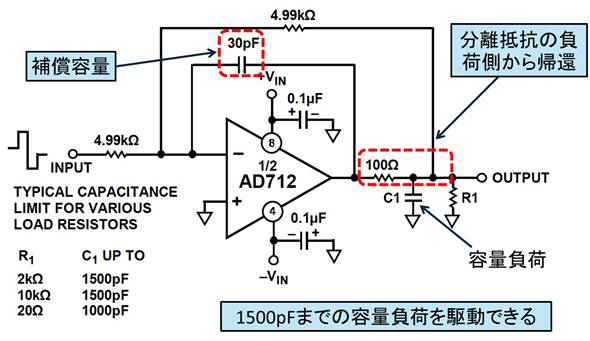
図16は高度な「二重帰還補償」というものです．

高度な手法ため，またSPICEシミュレーションでもOPアンプのモデルの不正確さが原因で適切な定数算定が難しいため，ここではコンセプトだけを示します．

この図はAD712のデータシートから抜粋したものです．分離抵抗と同じコンセプトで負荷容量を分離しますが，分離抵抗の負荷側からOPアンプの反転入力に帰還し，出力と入力間にも補償容量を接続して二重に帰還をかけます．AD712のデータシートの記述によると，これにより1500pFの容量負荷を駆動できるとあります．

6．位相余裕の理論的意味あいと確認方法

第4節で回路の応答と位相余裕との関係を示しました．ここでは最後の事項として，位相余裕の理論的意味あいと確認方法について説明します．

6.1　ループ・ゲインを定義する

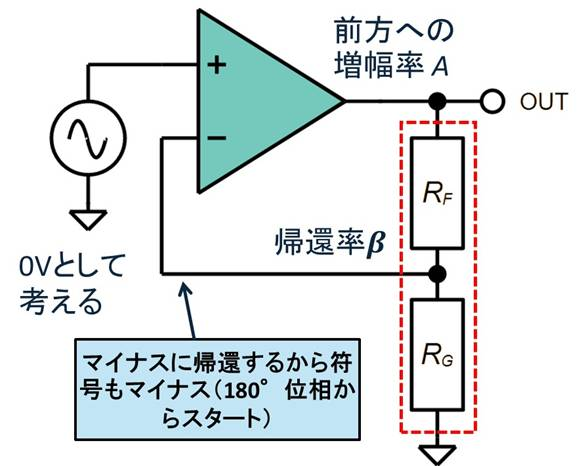
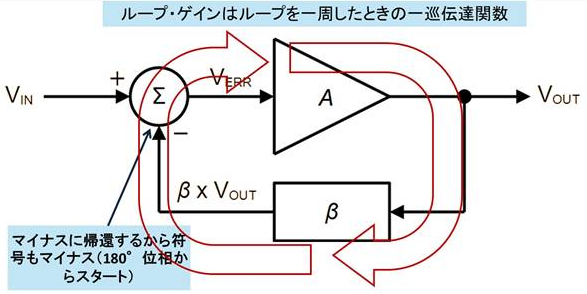
位相余裕の評価には，OPアンプの回路を「帰還モデル」として取り扱い，これから「ループ・ゲイン」というものを定義することがスタートです．図17に非反転増幅回路とそのループ・ゲインを定義するための補足を記載したものを示します．

OPアンプのオープン・ループ・ゲインを前方への増幅率$A$とし，帰還率$\beta$を，

\begin{align*} \beta = \frac{R_G}{R_G + R_F} \end{align*}

とします．この帰還率$\beta$は出力から反転入力へ帰還される$R_F$と$R_G$で形成される抵抗分圧比で，回路の動作ゲインの逆数になります．これからループ・ゲイン$T$を，

\begin{align*} T = - A \beta = - A \frac{R_G}{R_G + R_F} \end{align*}

として定義します．極性がマイナスなのは，反転入力に帰還しているからです．このループ・ゲインは系を信号が一巡するときのゲインで，図18のように考えることができます（「一巡伝達関数」とも呼ぶ）．

6.2　ループ・ゲインをシミュレーションし位相余裕を得る

「$- A \beta$であるなら，フィードバック経路を切断して図18の$V_{ERR}$から信号を注入し，ブロック$\beta$の出力$\beta \times V_{OUT}$をシミュレーションしたり実測したりすればいいだろう」と思うかもしれません．

しかしフィードバック経路を切断して，ループ・ゲインをシミュレーションや実測はできません．これは回路が非常に大きなゲイン（オープン・ループ・ゲイン）で動作しているため，入力オフセット電圧などで出力が振り切ってしまうからです．

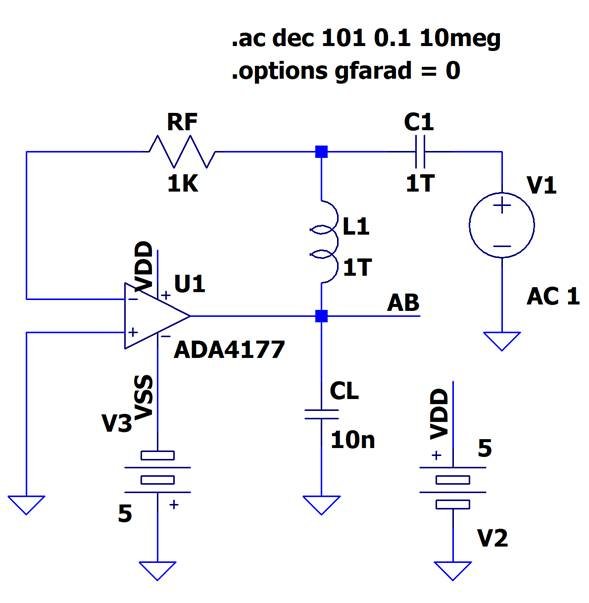
そこでシミュレーションでは見かけ上ループを閉じます．図19にこの回路を示します（ループを閉じるため，高いインダクタンス$L_1$を挿入している）．図6に示したADA4177-2で10nF（0.01$\mu$F）を駆動する例です．実測の方法については後述します．

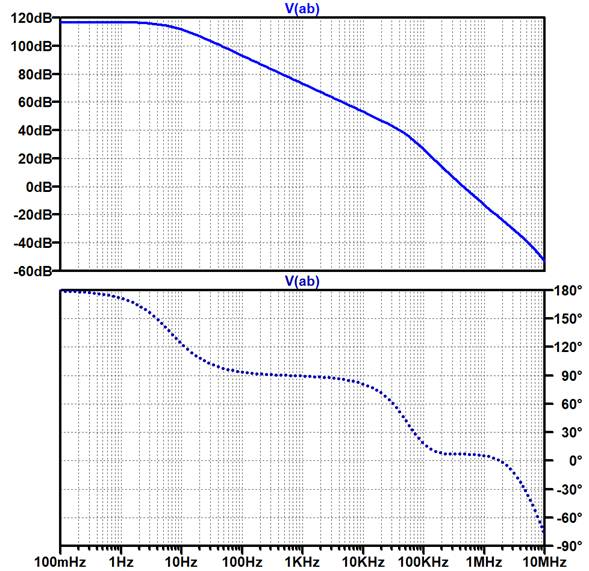
$V_1$から大きな容量$C_1$を通じて信号を印可します．端子ABを測定するとループ・ゲイン$T$が得られます．この結果を図20に示します．回路入出力の動作ゲインとはまったく異なるカーブ形状になっています．

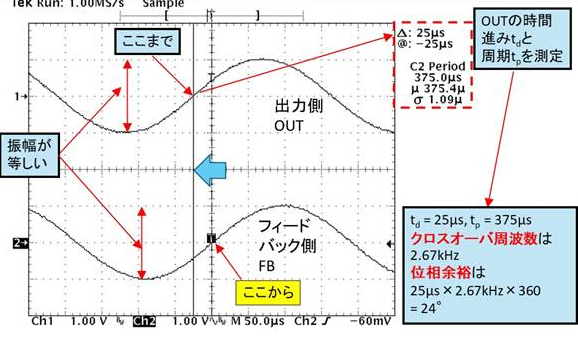
ここから位相余裕を求めることができます．位相余裕はループ・ゲイン$T$の大きさが0dB（$=$1）になったとき（これを「クロスオーバ周波数」と呼ぶ），0°位相（正帰還状態つまり発振状態）からどれだけ離れているかを示すものです．これが第4節に示したように40° ～60°程度が必要になります．

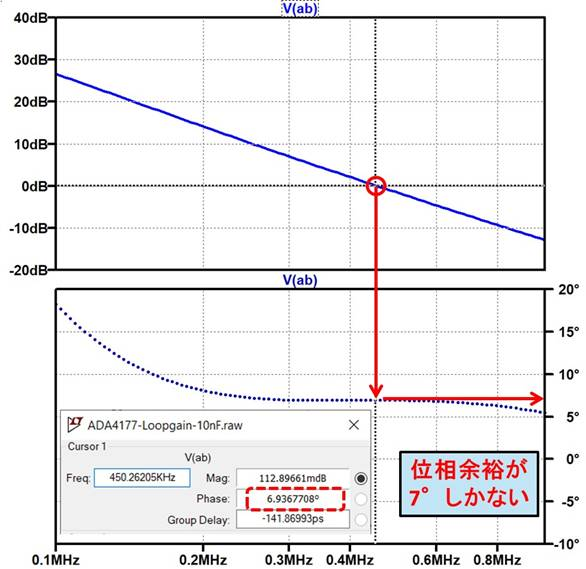
図20を拡大し，マーカを設定したものを図21に示します．ADA4177-2で10nF（0.01$\mu$F）を駆動する例（図6～図8）では位相余裕が7°しかなく，かなり不安定（異常発振寸前）だとこの結果からわかります．

6.3　実測で位相余裕を得る方法

実務では，第4節の図9や図10で示した矩形波応答や周波数特性測定で大きなリンギングやピーキングが出ていないことを確認すれば十分でしょう．それでも実測でループ・ゲインや位相余裕を求めたいとすれば，先に示したようなインダクタや容量は使用できません．

そこで実測ではFrequency Response Analyzer（FRA）という測定器（図22）を用います．

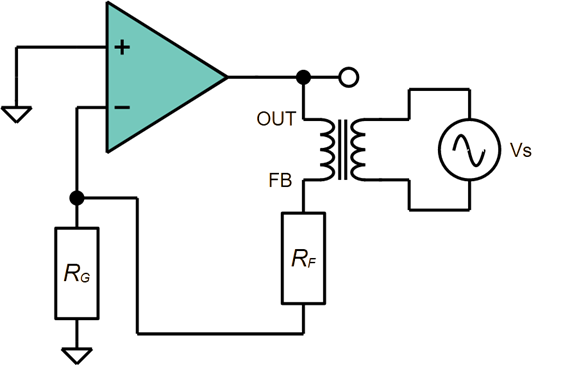
ただ単純に位相余裕だけを測定したいのであれば，図23のような構成でトランスを用いてフィードバック経路に電圧源を挿入することで実現できます．

測定はトランス両端のOUTとFBの電圧を観測しながら，それぞれの振幅が同じになる周波数に発振器を設定して，図24のように算出します．

これらの測定方法は「電圧注入法」と呼ばれるものですが，それでも出力側のインピーダンス$Z_{OUT}$と帰還入力側のインピーダンス$Z_{FB}$が，

\begin{align*} R_{OUT} \ll R_{FB} \end{align*}

である必要性があります．

図6や図19で示した容量負荷のある回路は，周波数が上昇してくると$Z_{OUT}$が上昇し，$Z_{FB}$が低下するため，上記の式の関係を維持することができなくなり，誤差が大きくなります．この辺の話題は話しが長くかつ本格的になりますので，興味あるかたは参考文献に示す資料を入手し，ご覧になることをお勧めします．

最後に

古くから，「OPアンプ増幅回路を作ると発振器になり，発振回路を作ると発振しない」というフレーズがあります．安定性を適切に評価し，不安定である心配があれば適切に対策することで，安定なOPアンプ増幅回路を作ることができます．

全4回にわたり，OPアンプ増幅回路について説明してきました．いくばくかでもご参考になれば幸いです．〈石井 聡〉

---

DigiKeyチャンネル「基本をがっちり！アナログ電子回路 30選」

YouTube「DigiKeyチャンネル」でも，本連載の著者 石井 聡 氏が，アナログ回路の重要ポイントをわかりやすく解説しています．全8回の動画を順次公開予定です．

OPアンプの基本的な使い方から高精度な計測回路の設計法まで，実際の回路例とともに学べる内容です．LTspiceによるシミュレーションと実測の比較もあり，理解が深まる内容です．アナログ回路を本気で学びたい方におすすめです．

　第1回　OPアンプの中身
　　第2回　OPアンプの基本回路
　　第3回　OPアンプの基本的な各種特性
　　第4回　オーディオ用回路
　　第5回　高精度計測回路
　　第6回　OPアンプで作る発振回路
　　第7回　電流電圧変換回路
　　第8回　OPアンプの安定性の確認と改善方法

〈ZEPエンジニアリング〉