微分方程式→伝達関数→状態方程式:動的システムのモデリング
ラズパイとPythonで一緒に!センサ・フュージョン入門
微分方程式は動的システムの出発点
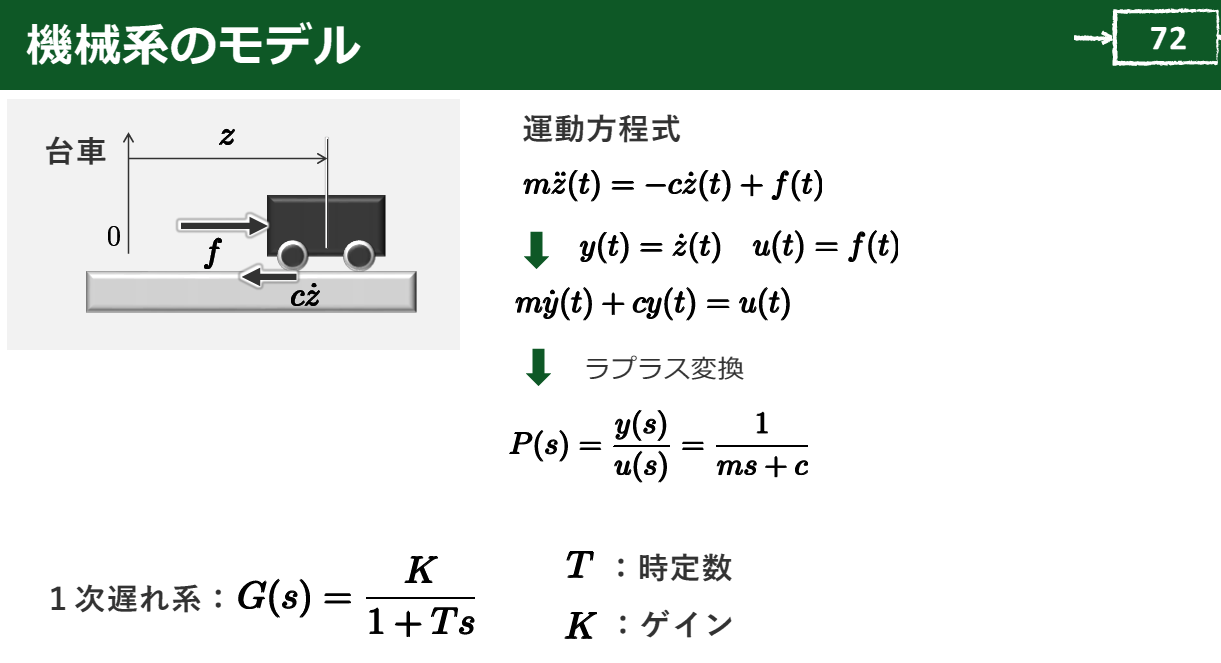
|
|---|
| 図1 微分方程式のままでは,時間領域での変化を追う必要があり,応答の特徴を直感的に比較しにくいため,別の表現へ変換する手順が使われる.画像クリックで動画を見る.または記事を読む.詳細はVOD/Pi KIT/data]ラズパイとPythonで一緒に!カルマン・フィルタ&センサ・フュージョン入門 |
動的システムのモデリングは,微分方程式から始まります.運動や電気回路,熱の伝達は,時間変化を含む関係として表されます.入力を $u$,出力を $y$ と整理すると,微分方程式は「入力が時間を通じて出力にどう影響するか」を示す記述です.この段階では,システムの物理的な意味が分かりやすく,質量や抵抗,摩擦といった要素が直接現れます.
一方で,微分方程式のままでは制御設計や解析が難しい場面があります.時間領域での変化を追う必要があり,応答の特徴を直感的に比較しにくいからです.このため,別の表現へ変換する手順が使われます.
伝達関数は入出力の関係を整理
微分方程式をラプラス変換すると,伝達関数という表現に変わります.ここでは初期値を $0$ と仮定し,入力と出力の関係だけに注目します.時間微分は複素変数に置き換えられ,微分方程式は代数的な形で整理されます.この変換によって,入力 $U$ と出力 $Y$ の比としてシステムの性質を表せます.
伝達関数は,周波数応答や安定性の議論に向いた表現です.入力に対して出力がどの程度増幅されるか,どの周波数で振る舞いが変わるかを一目で整理できます.制御器の設計では,この表現を使って応答の速さや振動の有無を検討します.
- 微分方程式:物理的意味を直接表す表現
- 伝達関数:入出力の関係を簡潔に示す表現
- 解析用途:安定性や応答特性の確認に向く
状態方程式は内部状態を明示
伝達関数は入出力の関係を示しますが,内部で何が起きているかは直接表しません.この内部の振る舞いを明示するのが状態方程式です.状態方程式では,システムの内部状態を変数として定義し,その時間更新を記述します.この表現は,動的システムが持つ「記憶」を明確にします.
状態方程式は,オブザーバやカルマン・フィルタといった状態推定の基盤です.ラズパイとPythonで制御や推定を実装する場合,離散時間の状態方程式として扱うことが一般的です.入力,状態,出力の関係が整理され,センサ・フュージョンとも結びつきやすい表現です.
- 状態:過去の影響を蓄えた内部変数
- 状態方程式:状態の更新と出力の関係を示す
- 推定と制御:同じ枠組みで扱える表現
表現を使い分ける設計の視点
微分方程式,伝達関数,状態方程式は,同じシステムを異なる視点で表したものです.物理理解には微分方程式,周波数特性の確認には伝達関数,推定や制御の実装には状態方程式が向いています.目的に応じて表現を切り替えることが,体系的な設計につながります.
ラズパイとPythonの環境では,これらの表現を行き来しながら設計を進められます.モデルを変換して理解を深めることが,動的システムを制御する力の基礎です.
〈ZEPマガジン〉参考文献
- [VOD/Pi KIT]MATLAB/Simulink×ラズパイで学ぶロボット制御入門,ZEPエンジニアリング株式会社.
- [VOD/KIT]MATLAB/Simulink×ラズパイで学ぶロボット制御入門,ZEPエンジニアリング株式会社.
- [VOD/Pi400 KIT]SLAMロボット&ラズパイ付き!ROSプログラミング超入門,ZEPエンジニアリング株式会社.
- [VOD/KIT]確率・統計処理&真値推定!自動運転時代のカルマン・フィルタ入門,ZEPエンジニアリング株式会社.
