お話 量子コンピュータ入門 その2
量子コンピュータの値は振幅1の球ベクトル
1と0の重ね合わせのイメージ
|
|---|
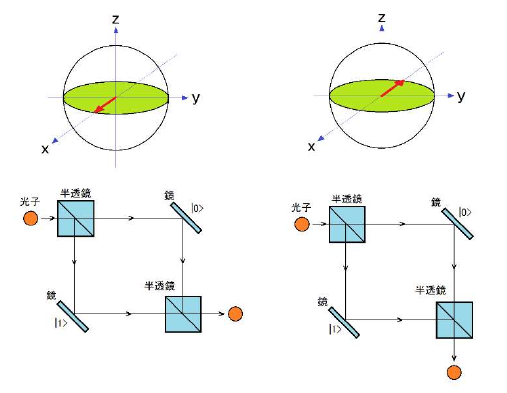
| 図1 古典的な1ビットが“0”または“1”で表されるのに対し,量子ビットは“0”と“1”の両方の状態を同時に保持する.これを「重ね合わせ」と呼ぶ.[著・提供]漆谷 正義.画像クリックで動画を見る.または記事を読む.詳細は[VOD/Pi KIT] Python×ラズパイで初めての量子コンピュータ |
量子ビットと球ベクトルの計算
重ね合わせと確率振幅
量子ビットは,古典的なビットが“0”または“1”で表されるのに対し,“0”と“1”の両方の状態を同時に保持できる点で異なります.これを「重ね合わせ」と呼び,状態は次のように表されます. \[ |\psi\rangle = \alpha |0\rangle + \beta |1\rangle \] ここで,$\alpha$ と $\beta$ は確率振幅と呼ばれる複素数であり,これらの絶対値の2乗がその状態の確率を表します.
球ベクトルとしての量子ビット
量子ビットの状態は,ブロッホ球と呼ばれる球面上のベクトルで視覚化できます.
この球面の任意の点が量子ビットの状態を表し,通常のビットが1次元の線上にあるのに対し,量子ビットは2次元の球面上に配置されます.これにより,量子ビットの状態は単なる“0”か“1”ではなく,状態ベクトルの振幅と位相で決定されます.
量子ゲートと量子演算
量子ビットの操作は量子ゲートを使って行います.
主な量子ゲートには,ビット反転の「Xゲート」,位相シフトの「Zゲート」,重ね合わせを作る「アダマールゲート(Hゲート)」などがあります.これらのゲートは線形代数の行列として表現され,量子ビットの状態ベクトルに適用されます. \[ H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \]
線形代数と量子ビット
量子ビットの動作や計算には線形代数学が欠かせません.量子ビットは“0”と“1”の状態をもつだけでなく,これらを重ね合わせた状態を保持できます.この重ね合わせの状態は,ケット・ベクトルというベクトルで表現されます.
例えば,量子ビットの状態は次のように表せます.
\[ |\psi\rangle = \alpha |0\rangle + \beta |1\rangle \]
ここで,$\alpha$ と $\beta$ は複素数であり,量子ビットの確率振幅と呼ばれます.
これらの絶対値の2乗がその状態が測定される確率を表します.量子ビットの状態はベクトルで表現され,量子ゲートはこのベクトルに作用する行列として定義されます.例えば,ビット反転を行う「Xゲート」や重ね合わせを作る「アダマール・ゲート(Hゲート)」などがあります.これらのゲートは状態ベクトルに行列を掛けることで量子ビットの状態を変化させます.
ブロッホ球とは
量子ビットの状態はブロッホ球と呼ばれる球体モデルで視覚化されます.
ブロッホ球は,量子ビットの状態を3次元空間で表現するための球体モデルです.量子ビットの振幅と位相が視覚的に理解しやすくするための表現です.量子ビットの状態は,この球体の表面上に配置され,球面上のどの位置も可能な状態を表します.
球面上の任意の点が量子ビットの状態を表し,線形代数学の行列演算を通じてこれらの状態を操作・制御できます.量子計算において,線形代数は量子ビットの基礎を支える重要な役割を果たしています.
量子ゲートとは
量子ビットの状態を変化させる操作を行います.ゲートは線形代数の行列で表現され,以下のように量子ビットの状態ベクトルに作用します
- Xゲート(ビット反転):ビットの“0”と“1”を反転する
- Zゲート(位相反転):状態の位相を180°シフトする
- アダマール・ゲート(Hゲート):ビットを重ね合わせ状態にする
これらのゲートは量子計算の基本的な操作であり,古典的なコンピュータでは実現できない並列計算が可能になります.〈著:ZEPマガジン〉
著者紹介
- 1971年 神戸大学大学院理学研究科修了
- 1971年 三洋電機株式に入社.レーザ研究,レーザ応用機器開発に従事.その後,ベータ,VHSビデオ開発,ディジタルビデオ・カメラ開発に従事
- 2009年 大分県立工科短期大学非常勤講師
- 2012年 西日本工業大学非常勤講師
- 2017年 大分大学工学部非常勤講師
著書
- [VOD/KIT] ラズパイ・キットで学ぶLinux I/Oボードの作り方・探し方・動かし方,ZEPエンジニアリング株式会社.
- [VOD/PiZero KIT]Python×ラズパイで初めての量子コンピュータ,ZEPエンジニアリング株式会社.
- 電子工作で始める量子コンピュータ,Interface,2019年3月号,CQ出版社.
参考文献
- [VOD/Pi KIT]ラズベリー・パイで学ぶLinux&Pythonプログラミング超入門,ZEPエンジニアリング株式会社.
- [VOD/KIT] 実習キットで一緒に作る!オープンソースCPU RISC-V入門,ZEPエンジニアリング株式会社.
- [VOD/Pi KIT]ラズベリー・パイで学ぶLinux&Pythonプログラミング超入門,ZEPエンジニアリング株式会社.
- [VOD/KIT]ラズベリー・パイで学ぶエッジAIプログラミング入門,ZEPエンジニアリング株式会社.
- [VOD/Pi KIT]SLAMロボット&ラズパイ付き!ROSプログラミング超入門,ZEPエンジニアリング株式会,ZEPエンジニアリング株式会社.社.
- [VOD/Pi KIT]ラズパイ×Pythonで動かして学ぶモータ制御入門
- [VOD/Pi KIT]MATLAB/Simulink×ラズパイで学ぶロボット制御入門,ZEPエンジニアリング株式会社.
- [VOD/KIT]ラズパイ×Node-REDで作ろう!IoTアプリ開発入門,ZEPエンジニアリング株式会社.
