【Digi-Key社提供】フレッシャーズ＆学生応援特別企画

実験しながら学ぶフーリエ解析とディジタル信号処理
[Vol.1　フーリエ解析の基本「三角関数」の正しい理解]

スペクトル解析やディジタル・フィルタを最適化してSTM32マイコンに実装

著者・講師：別府伸耕/Nobuyasu Beppu (リニア・テック)
企画編集・主催： ZEPエンジニアリング株式会社

関連製品：［VOD］Pythonで学ぶやりなおし数学塾1【微分・積分】
関連製品：［VOD］Pythonで学ぶやりなおし数学塾2【フーリエ解析】
関連製品：［VOD］Pythonで学ぶマクスウェル方程式【電場編】＋【磁場編】
関連製品：［VOD/KIT］STM32マイコン＆Wi-Fiモジュールで学ぶ C/C++プログラミング入門
関連記事：Pythonではじめる数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
関連記事：Pythonではじめる数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]

【Index】

Vol.1　フーリエ解析の基本「三角関数」の正しい理解

Vol.2　STM32マイコンの開発環境を準備する

Vol.3　「フーリエ級数」を利用して波形を合成する実験

Vol.4　「フーリエ級数」にもとづいて波形を分析する実験

ディジタル信号処理の本質をマイコンで学ぶ

誰もがディジタル信号処理を活用すべき時代


（a）システムの全体図	（b）LEDマトリクスにスペクトルを表示した様子
写真1　ワンチップ・マイコンを使ったディジタル信号処理システムの一例

計算処理を実行してこそ「コンピュータ」は真価を発揮する

半導体技術の発展により，高性能な「ワンチップ・マイコン」（one-chip microcomputer，以下「マイコン」）が数100円程度で入手できるようになりました．マイコンは，簡単なシステムの制御やユーザ・インターフェースの実装などにとても便利です．しかし，これらの用途にはそこまで高度な演算性能は必要ありません．

演算性能が高いマイコンがその真価を発揮するのは，「コンピュータ」という名前のとおり「計算機」として使われたときです．せっかく高性能なマイコンを安価に入手できるならば，その高度な演算性能こそ享受すべきです．演算処理を実行しないならば，いくら高性能なマイコンを持っていても宝の持ち腐れになってしまいます．

ディジタル信号処理の例：高速フーリエ変換

マイコンを使ったシステムと相性が良い計算処理にはいろいろな種類がありますが，その代表例として「ディジタル信号処理」（digital signal processing）が挙げられます．写真1の「オーディオ用スペクトル・アナライザ」は，マイコンを使ってディジタル信号処理システムを構成した一例です．

このシステムはコンデンサ・マイクで拾った音声信号をアンプで増幅し，その信号をマイコンのAD変換器に入力しています．マイコンはこの音声データを対象として「高速フーリエ変換」と呼ばれる演算を実行します．この演算を行うと，入力された音声データに含まれる音の周波数分布（周波数スペクトル）を求めることができます．演算結果として得られた周波数スペクトルは，写真1(b)のLEDマトリクスに表示されます．マイクは右と左の2個あるので，周波数スペクトルもそれぞれに対応したものが表示されます．

この「オーディオ用スペクトル・アナライザ」は信号処理のデモ用に作った一種のアクセサリですが，これ以外にも「高速フーリエ変換」の応用先は非常に多岐にわたります．

ディジタル信号処理を学べば付加価値を上げられる

開発コストが下がったことで差別化が困難になった

半導体メーカ各社の努力により高性能なマイコンの単価は下げられ，マイコンの評価ボードは低価格で供給されています．さらに，開発環境のソフトウェアですら無償で提供されるという状況になっています．マイコンを応用した製品開発のコストは，下がるところまで下がったという感触があります．

しかし，これは同時に「物だけで価値を生み出す」ことが難しくなったことを意味します．開発コストが下がった分だけ製品の陳腐化は避けがたくなり，他と差別化を図るのも難しくなります．

演算処理が製品に価値を吹き込む

このような状況において，マイコン回路に価値を吹き込むのは「信号処理の内容」です．解決すべき問題に対して適切な信号処理のアルゴリズム（計算手法）を選択し，それを効率よくマイコンに実装することができれば，製品の付加価値は大きく上がります．

誰もが簡単にマイコンを入手して開発できるようになったことで，誰もがディジタル信号処理を「読み書きそろばん」のレベルで使いこなすことが求められる時代になったと言えます．信号処理を活用できるようになれば，確実に製品の付加価値を上げられます．また，これを学んだエンジニア自身の市場価値も大きく向上するでしょう．

ディジタル信号処理の本質は「フーリエ解析」にある


図1　ディジタル信号処理はフーリエ解析の枠組みの一部であると考えられる

信号処理とは「数学」である

マイコンで扱う信号処理の実態は，「要求される機能を数式の形で展開してそれをディジタル数値の演算として実行する」というものです．実際の開発では「数式をそのまま忠実に実行するプログラムを書く」ことになるので，プログラミングの知識だけではなく数学の理解も必須となります．

今は便利なライブラリが揃っているので数学に対する深い理解が無くても「何か動作するもの」を作ることはできますが，不具合が発生した場合の対処が困難になったり，かえって工数を浪費する結果になったりするのでお勧めはしません．やはり，数学を学んでから信号処理のプログラムを自分で書いてみるというのが正攻法になります．

以下，図1を見ながら一般的な「ディジタル信号処理」という分野を概観します．

周波数解析

一般的にディジタル信号処理で扱う内容は，「周波数解析」（frequency analysis）と呼ばれる体系に属しています．周波数解析は時間的に変化する信号を周波数成分に分解して扱う分野であり，よく使われるフィルタリング処理やスペクトル解析もこれに含まれます．

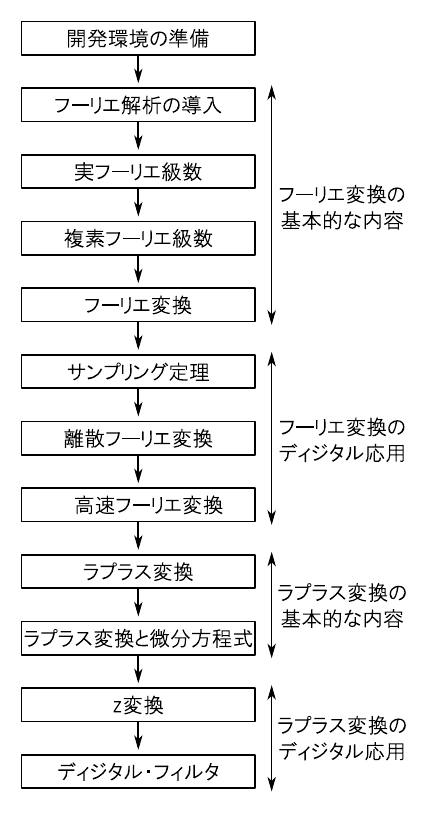
周波数解析は，「フーリエ解析」（Fourier analysis）という数学の分野によって裏付けられています．ディジタル信号処理（周波数解析）を意識してフーリエ解析の全体像を眺めると，図1のようになります．

フーリエ変換とラプラス変換

「フーリエ変換」（Fourier transform）は，フーリエ解析における中心的なテーマです．すべての信号処理はフーリエ変換から派生したものであると言っても過言ではありません．

また，フーリエ変換を変形させたものとして「ラプラス変換」（Laplace transform）という演算もあります．通常，エンジニアがラプラス変換を利用する目的はただ1つで，「（線形の）微分方程式を解くこと」です．これについては追ってラプラス変換を解説するときに触れます．

離散フーリエ変換とz変換

マイコンなどのディジタル回路で扱う信号は，何らかの時間間隔（あるいは空間的な間隔）でぶつ切りにされた「離散信号」（discrete signal）です．このような信号のことを「サンプリングされた信号」と表現することもあります．

数学の理論としてのフーリエ変換やラプラス変換では，時間的に（あるいは空間的に）連続した「連続信号」（continuous signal）を扱います．そのため，マイコンのプログラムとして実装するためにはフーリエ解析の各種演算を「離散化」（discretization）する必要があります．フーリエ変換を離散化したものは，「離散フーリエ変換」（discrete Fourier transform: DFT）と呼ばれています．また，ラプラス変換を離散化したものは「z変換」（z transform）といいます．

FFTとディジタル・フィルタ

マイコンでフーリエ変換を実行する場合は，離散フーリエ変換を変形した「高速フーリエ変換」（fast Fourier transform: FFT）と呼ばれるアルゴリズムがよく使われます．FFTは，DFTと比べて桁違いに短い時間で処理を実行できる利点があります．

また，z変換を利用すると信号の中から必要な周波数成分だけを取り出す「ディジタル・フィルタ」（digital filter）を作ることができます．z変換は，他にもシステムの微分方程式（差分方程式）と関係した様々な応用が可能です．

フーリエ解析はあらゆる分野で核心的な役割を担っている

フーリエ変換やラプラス変換をはじめとするフーリエ解析の理論は，「音声処理」や「画像処理」，「制御理論」，「ディジタル無線」，「計測機器」，さらには「確率・統計」など，あらゆる分野において欠かせない役割を担っています．先端技術の核心は，フーリエ解析なしには理解することができません．

これだけ応用分野に富むフーリエ解析を学ばずにいるのは，非常にもったいないことです．自分の仕事と直接関係なさそうだと思っていても，どこかで必ずフーリエ解析の理論とつながっています．フーリエ解析は，エンジニアリングにおいてまさに「空気」のような存在であると言えます．

フーリエ解析をマイコンに実行させる

自分でディジタル信号処理を実装することを目指す

本連載では，フーリエ解析の理論をできるだけ丁寧に解説していきます．フーリエ解析で登場する主要な演算を理解し，最終的にはディジタル信号処理のプログラムを自分で書けるようになることを目指します．

フーリエ解析を学ぶには，数式を読み解くことが必要となります．数式の解説はどうしても抽象的な議論になりがちなので，とっつきにくいと感じられるかもしれません．そこで，数式を用いた解説とあわせてマイコンによるプログラム例を示し，実際に演算処理を試しながら話を進めていくことにします．自分の手で実験しながら読み進めれば，抽象的な理論と具体的な実装をバランスよく理解し，技術を自分のものにできるはずです．なお，プログラミング言語はC言語（一部C++）を使います．

フーリエ解析の理論を体系的に理解する

図2に，本連載の流れを示します．はじめにマイコンの開発環境を整えてから，本題であるフーリエ解析の理論に入っていきます．

最初の目標は「フーリエ変換」を理解することです．フーリエ変換は，あらゆる信号処理の土台になります．続いて，離散信号を扱う上で重要となるサンプリング定理や，マイコン上でフーリエ変換を実行するアルゴリズムである「高速フーリエ変換」を扱います．

フーリエ変換の解説が終わったら，「ラプラス変換」に進みます．ラプラス変換は微分方程式との関りが深い演算なので，線形システムの取り扱いとあわせて解説します．ラプラス変換の基本をおさえたら，「z変換」や「ディジタル・フィルタ」といった信号処理でよく使われる手法について解説します．


図2　本連載の流れ．大きく分けて4つの部分で構成されている

コラム1　ディジタル信号処理と微分方程式

エンジニアが開発の現場で扱うシステムには，ロボットや電気回路など様々なものがあります．原理的には，これらのシステムの挙動は「ニュートンの運動方程式」や「マクスウェル方程式」といった「微分方程式」で表現されます．このことから，微分方程式はエンジニアが「設計」をする際の頼もしい味方であると言えます．

もともと，フーリエ解析という分野は微分方程式を扱いやすくするために生まれました．特に，ラプラス変換は様々な線形微分方程式を解く手法として広く使われています．フィルタ回路やフィードバック系の設計でラプラス変換を使ったことがある方も多いかと思います．

また，コンピュータ上で微分方程式を解くプログラムは「ソルバ」（solver）や「シミュレータ」（simulator）などと呼ばれていますが，これらの中には高速フーリエ変換やz変換を活用したものがあります．よって，ディジタル信号処理を学んでおけばシミュレーションに対する知見も広がります．これは，おおもとのフーリエ解析が微分方程式を解くためのテクニックであることを考えれば納得できるかと思います．

本連載で使用するSTM32系マイコンの紹介

ディジタル信号処理を学ぶための道具をそろえる

STマイクロエレクトロニクス社のマイコンと開発環境を利用する

本連載では「マイコンとして広く普及している」，「評価ボードを安価で購入できる」，「使いやすい開発環境が無償で手に入る」といった理由により，STマイクロエレクトロニクス社製の“STM32”系のマイコンを使うことにします．


（a）“NUCLEO-F446RE”ボード	（b）USB Type A - Mini B ケーブル

（c）プログラムの統合開発環境“STM32CubeIDE”	（d）プログラム書き込みツール“STM32CubeProgrammer”
図3　本連載で使うマイコンと開発環境．この4つがあればすぐに開発を始められる

図3（a）のマイコン・ボード本体，図3（b），図3（c），図3（d）の書き込みツールの4つを揃えれば，これから紹介する実験をすぐに始めることができます．

NUCLEO-F446REボード

図3（a）に，これから使うマイコン・ボードを示します．このボードはSTマイクロエレクトロニクス社が販売している“NUCLEO”（ニュークレオ）シリーズの評価ボードの1つで，“NUCLEO-F446RE”という型番のものです．

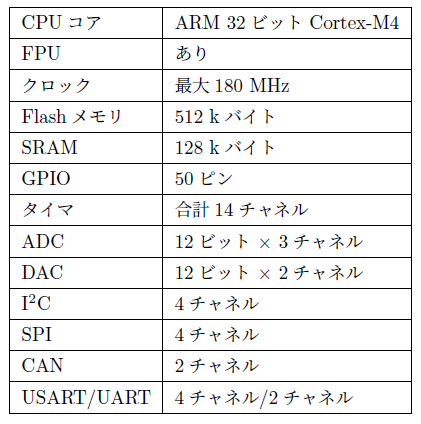
このボードには“STM32F446RET6”という型番のワンチップ・マイコンが搭載されています．このマイコンの主な仕様を表1に示します．クロックは最大180 MHzで，“FPU”（floating point unit，浮動小数点演算装置）も搭載されており，ちょっとした実験や製品に組み込むには十分な性能です．

また，“ADC”（analog to digital converter，アナログ・ディジタル変換器）や“DAC”（digital to analog converter，ディジタル・アナログ変換器）といったアナログ・インターフェースも備えています．さらに，“UART”（universal asynchronous receiver/transmitter，汎用非同期送受信機）や“$\mathrm{I^2 C}$”（inter integrated circuit，集積回路間通信），“SPI”（serial peripheral interface，シリアル式周辺回路インターフェース）といった周辺機器と接続するための各種インターフェースも豊富にあります．

STM32系のマイコンにはいろいろな種類のものがありますが，今回使う“STM32F446RET6”は全体的にバランスのとれた使いやすいマイコンであると言えます．


表1　“STM32F446RET6”の主な仕様

プログラムの作成には無償の開発環境を使う

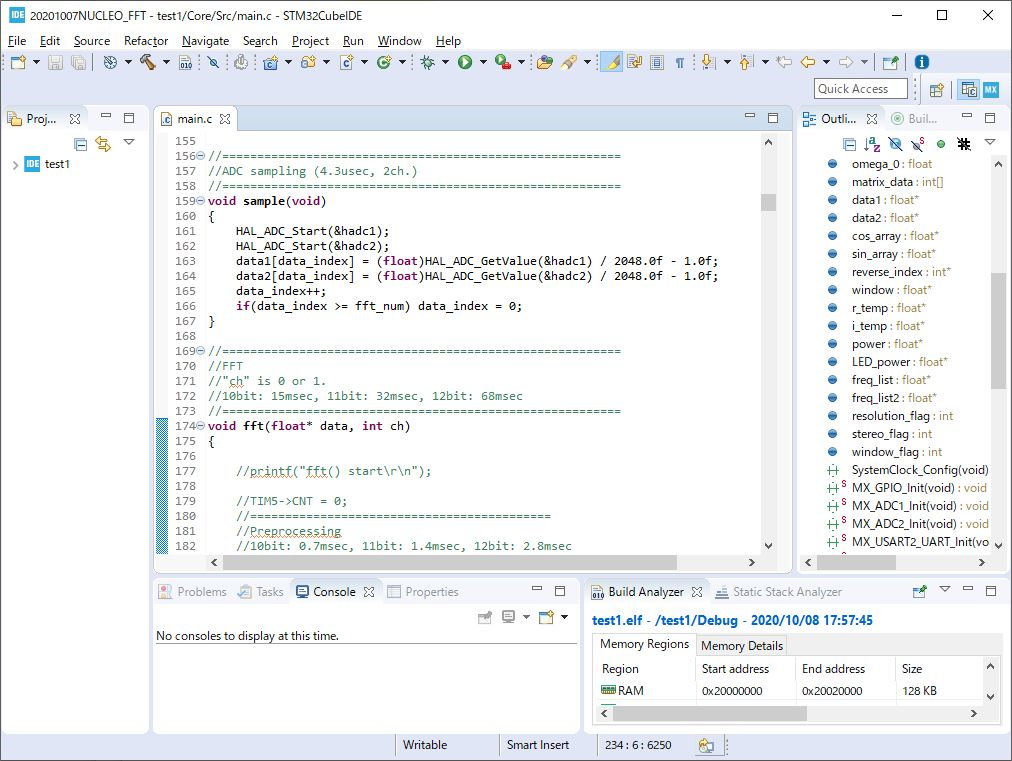
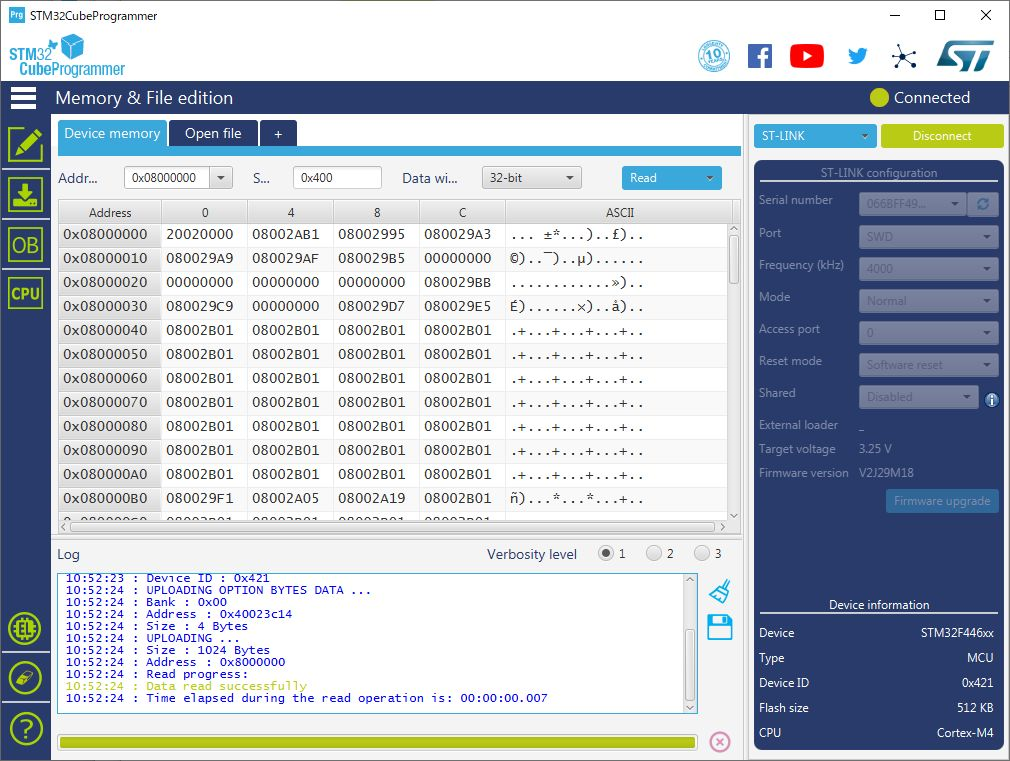
マイコンのプログラムを開発するソフトウェアは，STマイクロエレクトロニクス純正の“STM32CubeIDE”を使います（図3（c）．また，マイコンにプログラムを書き込むソフトウェアは“STM32CubeProgrammer”を使います（図3（d））．これらのソフトウェアは無償で入手できます．具体的なインストール手順は[Vol.2　STM32マイコンの開発環境を準備する]を参照してください．また，実際にこれらの開発環境を使って簡単なプログラムを作る手順も[Vol.2　STM32マイコンの開発環境を準備する]で解説しているので，初めてSTM32系のマイコンを使う場合はそちらも参照してください．

上記のソフトウェアの他に，マイコンから送られてきたシリアル通信のデータを表示するために“Tera Term”を使用します（Tera Termのインストール方法も[Vol.2　STM32マイコンの開発環境を準備する]で解説しています）．また，パソコン側でデータを整理したりグラフを描いたりする作業は“Excel”で行います．説明では“Excel 2019”を使っていますが，他のバージョンでも構いません．

フーリエ解析の主役である三角関数の復習

高校数学の復習から始める

これからフーリエ変換やラプラス変換，そこから派生した離散フーリエ変換やz変換について解説していきますが，これらの演算において中心的な役割を果たすのが「三角関数」（trigonometric function）です．

三角関数はディジタル信号処理にとどまらず電気回路理論や古典制御理論，さらには確率・統計といった分野にも登場し，常に重要な役割を果たします．これらの理論を使いこなす上で三角関数を避けて通ることはできません．そこで，ここでは高校数学で習う三角関数の定義から出発し，三角関数に関する重要な項目について確認することにします．

三角関数の定義

三角関数のもとになった「三角比」（trigonometric ratios）は，「角度と長さを結び付ける道具」として考案されたものです．三角関数もその性質を受け継いでいます．三角関数を扱うときは，図形的な「長さ」（座標）に着目して考えると理解しやすくなります．

サインとコサイン

図4のように半径が“1”の円を考えます．このような円を「単位円」（unit circle）といいます．単位円の円周上にある点“$\mathrm{P}(x,y)$”を考え，$x$軸から点Pを見た角度を“$\theta$”とします．この点Pの$x$座標を“$\cos (\theta)$”，$y$座標を“$\sin (\theta)$”と定義します．

\begin{align} x &= \cos(\theta)\\ y &= \sin(\theta) \end{align}

この定義と「三平方の定理」より，次式が得られます．

\begin{equation} \cos^2(\theta)+\sin^2(\theta) = 1 \end{equation}

また，図4を利用すると次の2式が成り立つことがわかります．

\begin{align} \sin(-\theta) &= -\sin(\theta)\\ \cos(-\theta) &= \cos(\theta) \end{align}


図4　三角関数の定義．単位円上の点Pの$x$座標を$\cos(\theta)$，$y$座標を$\sin(\theta)$と定義する

タンジェント

図4において“$y/x$”という「長さの比」を考え，この値を“$\tan(\theta)$”と定義します． \begin{equation} \cfrac{y}{x} = \cfrac{\sin(\theta)}{\cos(\theta)} = \tan(\theta) \end{equation} 「三角形の辺の長さの比」は他にも何種類か定義できますが，一般的に使われるのは“$\sin$”，“$\cos$”，“$\tan$”の3つです．これらは角度“$\theta$”に対応して変化するので，「角度$\theta$の関数」になっています．このことを明示するために，“$\sin(\theta)$”のように関数の名前の後に括弧を付けて変数“$\theta$”を表記しています．これは，C言語の文法と同じです．

角度の単位は「ラジアン」を使う

三角関数で扱う角度“$\theta$”の単位は「ラジアン」（radian）です．「度」（degree）は使いません．

「度」は，「地球では1年が約360日だから円周を360分割したものを1度としましょう」ということで定められました．私たち地球人の生活には馴染むかもしれませんが，数学的に意味のある単位の定め方ではありません．

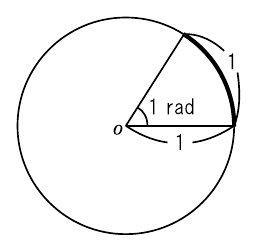
これに対して，「ラジアン」は「円周の長さ」に着目して定められた角度の単位です．単位円上の弧の長さが“1”になるときの中心角を“1 rad”として定義します（図5）．

もし中心角に対応する単位円上の弧の長さが“$x$”ならば，その中心角の角度は“$x$ rad”となります．また，単位円の円周全体の長さは“$2\pi$”なので次式が成り立ちます．

\begin{equation} 360^{\circ} = 2\pi \, \mathrm{rad} \end{equation}

今後は特に明示しませんが，角度の単位はすべて「ラジアン」に統一して扱います．


図5　三角関数を扱うときは角度の単位として「ラジアン」（rad）を使う

三角関数のグラフ

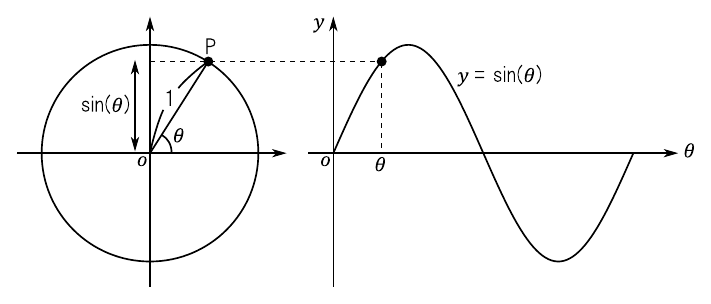
“$\sin(\theta)$”とは，単位円上を動く点Pの「$y$座標」の値でした．図6のように角度“$\theta$”を変化させたときにPが動く軌跡をイメージすれば，$\sin(\theta)$のグラフを描くことができます．

また，$\cos(\theta)$のグラフも点Pの$x$座標の軌跡として同様にイメージすることができます．今後は，$\sin$と$\cos$のグラフを合わせ「正弦波」（sine wave）と呼ぶことにします．


図6　$y=\sin(\theta)$のグラフ．単位円上の点の軌跡になっている

マイコンを使って正弦波のグラフを描く実験をする

プログラムを書いてコンパイルする

マイコンを利用して，自分で正弦波のグラフを描いてみましょう．

STM32CubeIDEで新しいプロジェクトを作ります．具体的な手順は[Vol.2　STM32マイコンの開発環境を準備する]を参照してください．“main.c”のソース・コードを開き，冒頭部分でリスト1のように“stdio.h”および“math.h”をインクルードしてください．今後作成するプログラムでは，特に明示しなくても常にこれらのヘッダ・ファイルをインクルードするものとします．

/* USER CODE BEGIN Includes */
#include "stdio.h"
#include "math.h"
/* USER CODE END Includes */

リスト1　ソース・コードの冒頭部分で“stdio.h”と“math.h”をインクルードする

`/* USER CODE BEGIN Includes / #include "stdio.h" #include "math.h" / USER CODE END Includes */`
リスト1　ソース・コードの冒頭部分で“stdio.h”と“math.h”をインクルードする

続いて，main()関数の部分をリスト2のように記述してください．リスト2では“printf()”関数を使っていますが，printf()関数を使えるようにする準備については[Vol.2　STM32マイコンの開発環境を準備する]を参照してください．プログラムが完成したら，問題なくコンパイルできることを確認してください．

なお，これ以降もプログラムのリストはmain()関数の部分のみ記載します．main()関数以外の部分（クロックやGPIOの設定など）は，特に指定しない場合は[Vol.2　STM32マイコンの開発環境を準備する]で解説している状態のまま変更しないものとします．

  /* USER CODE BEGIN 2 */
  int i; //loop index
  float sin_array[100]; //sin data array
  float delta = 2*M_PI/100;
  //initialize the array
  for(i=0; i<100; i++)
  {
	  sin_array[i] = sin(delta * i);
  }
  //print
  for(i=0; i<100; i++)
  {
	  printf("%f\r\n", sin_array[i]);
  }
  /* USER CODE END 2 */





リスト2　1周期分の$\sin(\theta)$の値をUARTで出力するプログラム

`/* USER CODE BEGIN 2 / int i; //loop index float sin_array[100]; //sin data array float delta = 2M_PI/100; //initialize the array for(i=0; i<100; i++) { sin_array[i] = sin(delta * i); } //print for(i=0; i<100; i++) { printf("%f\r\n", sin_array[i]); } /* USER CODE END 2 */`
リスト2　1周期分の$\sin(\theta)$の値をUARTで出力するプログラム

ソース・コードの解説

“sin_array[]”という配列を用意して，$\sin(\theta)$の値を1周期分格納しています．今回は1周期（$2\pi = 2 * \mathrm{M\_PI}$）を100分割した値を“delta”という変数に格納し，この値を刻み幅として$\sin(\theta)$のデータを作っています．作成したsin_array[]のデータは，printf()関数を使ってUARTから出力しています．

Tera Termで計算結果を受信する

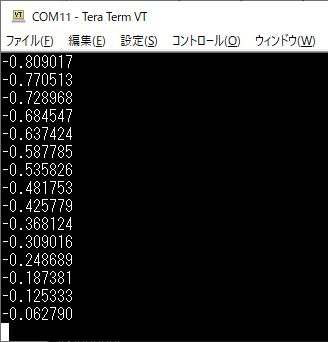
マイコンにバイナリ・ファイルを書き込んだら，Tera Termを起動します．Tera Termのメニュー・バーから[編集]-[バッファのクリア]をクリックして，それまでの受信内容を消去しておきます．この状態でNUCLEOボードのリセット・ボタンを押すと，図7のように100個のデータが表示されます．この状態で[編集]-[全て選択]をクリックし，キーボードで[Ctrl] + [c]を入力してデータをコピーします．

Excelでグラフを描く

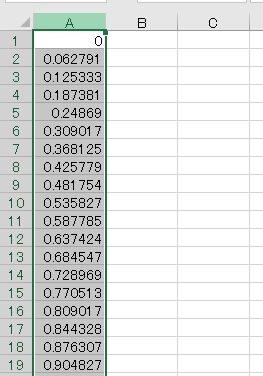
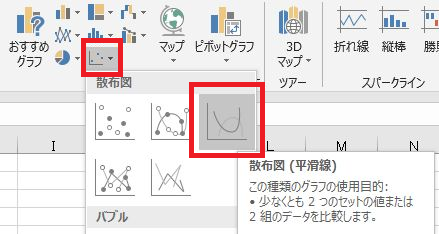
Excelを起動し，一番左上のセル（A1セル）を選択した状態でキーボードから[Ctrl] + [v]を入力します．先ほどコピーしたデータが貼り付けられたことを確認したら，続いてA列全体を選択します（図8．この状態で画面上部のメニュー・バーの[挿入]タブを選択し，「散布図（平滑線）」をクリックします（図9．図10のように1周期分の$\sin(\theta)$のグラフが表示されれば成功です．これ以降，グラフを描く時はこれと同様の手順で行うものとします．


図7　Tera Termで$\sin(x)$のデータを受信したようす	図8　Excelにデータを貼り付けて，全体を選択する


図9　データを選択した状態で「散布図（平滑線）」をクリックする	図10　Excelで$\sin(x)$のグラフを表示したようす

三角関数の加法定理

三角関数を扱う上で最もよく使う定理が，次の2式で表される「三角関数の加法定理」（trigonometric addition formulas）です．ここでは，これらの加法定理を導出します．これから何度も使う定理なので，ぜひ自分の手を動かして計算を追ってみることをおすすめします． \begin{align} \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) \\ \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) \end{align}

単位円上の弦“PQ”の長さを2通りの方法で表す

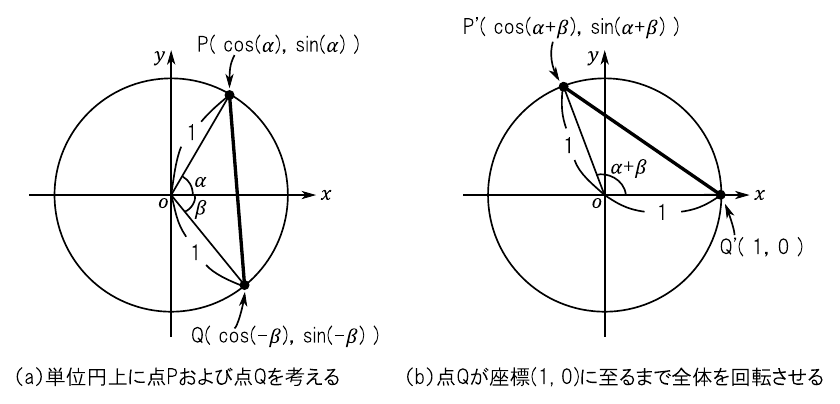
図11（a）のように，単位円上に点Pと点Qをとります．それぞれの点を$x$軸から見た角度を“$\alpha$”および“$\beta$”とします．このとき，弦PQの長さの2乗は「三平方の定理」より次のように求められます．

\begin{align} \label{eq:PQ_1} |\mathrm{PQ}|^2 &= \left\{ \cos(\alpha) - \cos(-\beta) \right\}^2 + \left\{ \sin(\alpha) - \sin(-\beta) \right\}^2 \nonumber \\ &= \left\{ \cos^2(\alpha)- 2\cdot \cos(\alpha) \cdot \cos(\beta) + \cos^2(\beta) \right\} \nonumber \\ &+ \left\{ \sin^2(\alpha) + 2\cdot \sin(\alpha) \cdot \sin(\beta) + \sin^2(\beta) \right\} \nonumber \\ &= 2 - 2 \cdot \left\{ \cos(\alpha)\cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) \right\} \end{align}

ここで，図11（b）のように図形全体を回転させて，点Qが点$(1,0)$と重なるようにします．この移動後の点を点P'および点Q'とします．点P'と点Q'の位置関係は図11（a）と同じなので，弦P'Q'の長さは弦PQと同じであり．したがって弦P'Q'に対応する中心角の大きさは“$\alpha + \beta$”となります．このとき，弦P'Q'の長さの2乗は「三平方の定理」より次のように表せます． \begin{align} \label{eq:PQ_2} |\mathrm{P'Q'}|^2 &= \left\{ \cos(\alpha + \beta) - 1 \right\}^2 + \left\{ \sin(\alpha + \beta) - 0 \right\}^2 \nonumber \\ &= \left\{ \cos^2(\alpha + \beta) - 2\cdot \cos(\alpha + \beta) + 1 \right\} + \sin^2(\alpha + \beta) \nonumber \\ &= 2 -2 \cdot \cos(\alpha + \beta) \end{align}


図11　加法定理の証明．弦PQの長さを2通りの方法で表す

cosに関する加法定理

弦PQと弦P'Q'の長さは等しいので，式（11）から次式が得られます． \begin{equation} \label{eq:cos_addition} \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) \end{equation}

これで「$\cos$に関する加法定理」を導出できました．

“$\theta + \pi/2$”に対する$\sin$と$\cos$の変換式

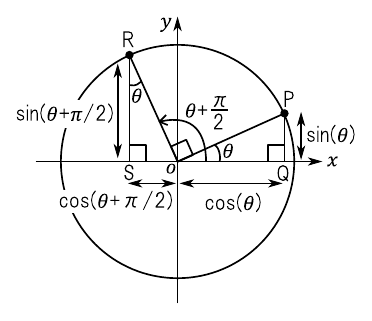
図12のように，単位円上に点Pと点Rをとります．$\mathrm{\Delta OPQ}$と $\mathrm{\Delta ROS}$は合同なので，$\sin$および$\cos$の定義から次の2式が得られます．

\begin{align} \label{eq:sin_pi_2} \sin(\theta) &= - \cos \left( \theta + \cfrac{\pi}{2} \right) \\ \label{eq:cos_pi_2} \cos(\theta) &= \sin \left( \theta + \cfrac{\pi}{2} \right) \end{align}


図12　角度が“$\theta+\pi /2$”のときの$\sin$および$\cos$の値を考える

$\sin$に関する加法定理

先に導出した「$\cos$に関する加法定理」において，“$\alpha$”の部分を“$\alpha + \pi/2$”に置き換えます．

\begin{equation} \cos \left( \alpha + \cfrac{\pi}{2} + \beta \right) = \cos \left( \alpha + \cfrac{\pi}{2} \right) \cdot \cos(\beta) - \sin \left( \alpha + \cfrac{\pi}{2} \right) \cdot \sin(\beta) \end{equation}

上式を式（13）および式（14）を利用して変形すると，次のようになります．

\begin{equation} -\sin(\alpha + \beta) = -\sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) \end{equation}

上式より，「$\sin$に関する加法定理」が得られます．

\begin{equation} \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) \end{equation}

三角関数の微分

微分の定義

「微分」（differential）という演算は，様々な関数の挙動を分析するためのとても便利な道具です．その本質は，「局所的な線形近似」であると言えます．

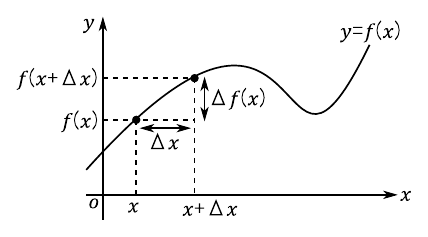
図13のように，何らかの関数“$f(x)$”があるとします．このとき，ある地点“$x$”における関数$f(x)$の「局所的な傾き」は次式で表せます．ただし，“$\Delta x$”は傾きを考えるための小さな幅をイメージしてください．

\begin{equation} \mathrm{「傾き」} = \cfrac{\Delta f(x)}{\Delta x} = \cfrac{f(x+\Delta x) - f(x)}{\Delta x} \end{equation}

ここで幅“$\Delta x$”を限りなく0に近づけると，本当の意味で「位置$x$における（ピンポイントの）傾き」を表現できると考えられます．すなわち，次のような極限を考えます．

\begin{equation} \cfrac{df(x)}{dx} = \lim_{\Delta x \to 0}\cfrac{f(x + \Delta x) - f(x)}{\Delta x} \end{equation}

上式で定義される演算のことを「微分」といいます．そもそも「傾き」というのは，「1次関数」すなわち「線形な関数」が持つパラメータです．これを様々な関数$f(x)$に対して考えようとしているので，微分という演算は「関数を局所的に線形だと見なして，その位置における傾きを求める操作」であると解釈できます．


図13　関数$f(x)$の「局所的な傾き」を考える

$\sin(x)$を微分する

「微分」の定義にもとづいて，関数“$f(x) = \sin(x)$”を微分すると次のようになります．なお，次式の計算では「加法定理」を使っています．

\begin{align} \label{eq:sin_diff_1} \cfrac{df(x)}{dx} &= \lim_{\Delta x \to 0}\cfrac{\sin(x + \Delta x)-\sin(x)}{\Delta x} \nonumber \\ &= \lim_{\Delta x \to 0} \cfrac{ \left\{ \sin(x)\cdot \cos(\Delta x) + \cos(x) \cdot \sin(\Delta x) \right\} -\sin(x) }{\Delta x} \nonumber \\ &= \lim_{\Delta x \to 0} \left\{ \sin(x) \cdot \cfrac{\cos(\Delta x) - 1}{\Delta x} + \cos(x) \cdot \cfrac{\sin(\Delta x)}{\Delta x} \right\} \end{align}

“$\sin(\Delta x)/\Delta x$”の極限

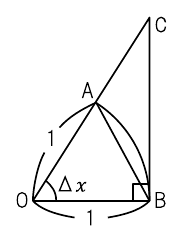
上式に現れた“$\sin(\Delta x)/\Delta x$”という形の極限について考えます．図14に示す$\mathrm{\Delta OAB}$の面積を“$S_1$”，弧OABの面積を“$S_2$”，$\mathrm{\Delta OCB}$の面積を“$S_3$”とします．これらの面積の面積を求めると，次のようになります．

\begin{align} S_1 &= \cfrac{1}{2} \cdot \left\{ 1\cdot \sin(\Delta x) \right\} \cdot 1 \nonumber \\ &= \cfrac{1}{2} \cdot \sin(\Delta x) \end{align} \begin{align} S_2 &= (\pi \cdot 1 \cdot 1) \cdot \cfrac{\Delta x}{2 \pi} \nonumber \\ &= \cfrac{1}{2} \cdot \Delta x \end{align} \begin{align} S_3 &= \cfrac{1}{2} \cdot \left\{ 1 \cdot \tan(\Delta x) \right\} \cdot 1 \nonumber \\ &= \cfrac{1}{2} \cdot \tan(\Delta x) \end{align}

これらの図形の面積には，“$S_1 < S_2 < S_3$”という大小関係が成り立ちます．よって，次式が得られます．

\begin{equation} \cfrac{1}{2}\cdot \sin(\Delta x) < \cfrac{1}{2} \cdot \Delta x < \cfrac{1}{2} \cdot \tan(\Delta x) \end{equation}

上式を変形すると，次式が得られます．

\begin{equation} \cos(\Delta x) < \cfrac{\sin(\Delta x)}{\Delta x} < 1 \end{equation}

上式において“$\Delta x \to 0$”の極限をとると，最左辺と最右辺がともに“1”になります．よって，「はさみうちの原理」より次式が得られます．

\begin{equation} \lim_{\Delta x \to 0} \cfrac{\sin(\Delta x)}{\Delta x} = 1 \end{equation}


図14　“$\sin(\Delta x)/\Delta x$”の極限を求めるために，図形の面積からアプローチする

“$\left\{ \cos(\Delta x) - 1 \right\}/\Delta x$”の極限

式（20）に現れた“$\left\{ \cos(\Delta x) - 1 \right\}/\Delta x$”という極限についても考えておきます．先に得られた“$\sin(\Delta x)/\Delta x \to 1$”という結果を利用すると，次式が得られます． \begin{align} \lim_{\Delta x \to 0} \cfrac{\cos(\Delta x) - 1}{\Delta x} &= \lim_{\Delta x \to 0} \cfrac{ \left\{ \cos(\Delta x) - 1 \right\} \cdot \left\{ \cos(\Delta x) + 1 \right\} }{\Delta x \cdot \left\{ \cos(\Delta x) + 1 \right\}} \nonumber \\ &= \lim_{\Delta x \to 0} \cfrac{\cos^2(\Delta x) - 1}{\Delta x \cdot \left\{ \cos(\Delta x) + 1 \right\}} \nonumber \\ &= \lim_{\Delta x \to 0} \cfrac{-\sin^2(\Delta x)}{\Delta x \cdot \left\{ \cos(\Delta x) + 1 \right\}} \nonumber \\ &= \lim_{\Delta x \to 0} - \left\{ \cfrac{\sin(\Delta x)}{\Delta x} \right\}^2 \cdot \Delta x \cdot \cfrac{1}{\cos(\Delta x) + 1} \nonumber \\ &= -(1)^2 \cdot 0 \cdot \cfrac{1}{1+1} \nonumber \\ &= 0 \end{align}

$\sin(x)$の導関数を求める

以上のことから，式（20）で表される「$\sin(x)$の微分」を実行すると次のようになります． \begin{align} \lim_{\Delta x \to 0} \cfrac{\sin(x + \Delta x) - \sin(x)}{\Delta x} &= \sin(x) \cdot 0 + \cos(x) \cdot 1 \nonumber \\ &= \cos(x) \end{align}

上式より，$\sin(x)$を微分すると“$\cos(x)$”が得られることがわかりました．このように，微分した結果得られる関数のことを「導関数」（derivative）}といいます．

$\cos(x)$の導関数を求める

$\sin(x)$を微分したときと同様の手順にしたがい，関数$f(x) = \cos(x)$の導関数も求めてみましょう．なお，次式の計算では「加法定理」を使っています．

\begin{align} \cfrac{df(x)}{dx} &= \lim_{\Delta x \to 0} \cfrac{\cos(x + \Delta x)- \cos(x)}{\Delta x} \nonumber \\ &= \lim_{\Delta x \to 0} \cfrac{ \left\{ \cos(x) \cdot \cos(\Delta x) - \sin(x) \cdot \sin(\Delta x) \right\} - \cos(x) }{\Delta x} \nonumber \\ &= \lim_{\Delta x \to 0} \left\{ \cos(x) \cdot \cfrac{\cos(\Delta x) - 1}{\Delta x} - \sin(x) \cdot \cfrac{\sin(\Delta x)}{\Delta x} \right\} \nonumber \\ &= \cos(x) \cdot 0 - \sin(x) \cdot 1 \nonumber \\ &= -\sin(x) \end{align}

上式より，$\cos(x)$を微分すると“$-\sin(x)$”が得られることがわかりました．

三角関数の微分をマイコンで計算する実験

“$\sin(x)$”を微分した値を求めるプログラム

マイコンを使って，関数“$f(x) = \sin(x)$”の微分を数値的に求める実験をしてみましょう．「微分」の定義にしたがって$\sin(x)$の微分を求める操作は，次式で表されるのでした．

\begin{equation} \cfrac{d}{dx} \sin(x) = \lim_{\Delta x \to 0} \cfrac{\sin(x + \Delta x) - \sin(x)}{\Delta x} \end{equation}

実際にマイコンで行う演算では“$\Delta x \to 0$”の極限を扱えないので，“$\Delta x$”として十分に小さい値を使うようにします．ここではリスト2に示したプログラムと同じく，「1周期の$2 \pi$を100分割した値」を“$\Delta x$”として使うことにします．

上式にしたがって$\sin(x)$の微分を求めるプログラムをリスト3に示します．

/* USER CODE BEGIN 2 */
  int i; //loop index
  float delta = 2*M_PI/100;
  float sin_array[100]; //sin data array
  float dsin_array[99]; //dsin/dx data array
  //initialize the array
  for(i=0; i<100; i++)
  {
	  sin_array[i] = sin(delta * i);
  }
  //differentiate
  for(i=0; i<99; i++)
  {
	  dsin_array[i] = (sin_array[i+1] - sin_array[i])/delta;
  }
  //print
  for(i=0; i<99; i++)
  {
	  printf("%f\r\n", dsin_array[i]);
  }
  /* USER CODE END 2 */





リスト3　$\sin(x)$を微分した値を出力するプログラム

`/* USER CODE BEGIN 2 / int i; //loop index float delta = 2M_PI/100; float sin_array[100]; //sin data array float dsin_array[99]; //dsin/dx data array //initialize the array for(i=0; i<100; i++) { sin_array[i] = sin(delta * i); } //differentiate for(i=0; i<99; i++) { dsin_array[i] = (sin_array[i+1] - sin_array[i])/delta; } //print for(i=0; i<99; i++) { printf("%f\r\n", dsin_array[i]); } /* USER CODE END 2 */`
リスト3　$\sin(x)$を微分した値を出力するプログラム

ソース・コードの解説

リスト2のプログラムと同様に，配列“sin_array[]”には$\sin$関数の値が格納されています．この配列に対して次式の演算を行い，近似的に「$\sin$関数の微分」を実行しています．計算結果は配列“dsin_array[]”に格納されます．なお，“$\Delta x$”の値は変数“delta”に対応しています．今回は“2*M_PI/100”という値に設定しています． \begin{equation} \cfrac{\sin(x + \Delta x) - \sin(x)}{\Delta x} = \cfrac{ \mathrm{ sin\_array[i + 1] - sin\_array[i] } }{\mathrm{delta}} \end{equation}

実行結果

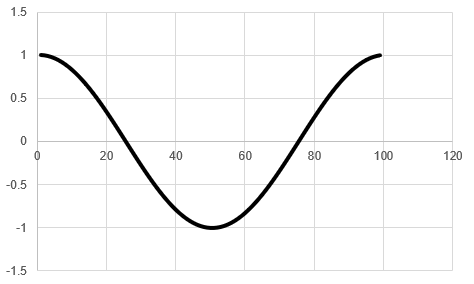
例によってTera Termを使って計算結果を受信し，Excelでグラフを描きます．図15のようなグラフが得られれば成功です．

図15は「$\cos(x)$のグラフ」になっています．これは，理論的に求めた「$\sin(x)$を微分すると$\cos(x)$になる」という結果と一致しています．

なお，今回は変数“delta”を「1周期 $2\pi$を100分割した値」に設定して実験をしましたが，もっと分割数を増やせば精度を向上させることができます．ただし，数値計算そのものによって生じる誤差もあるので，一概に分割を細かくすれば精度が上がるとは言えません．


図15　“$f(x)=\sin(x)$”を数値的に微分した結果．理論どおり$\cos(x)$のグラフが得られる

三角関数の積分

リーマン和

「微分」の次は，「積分」について考えます．

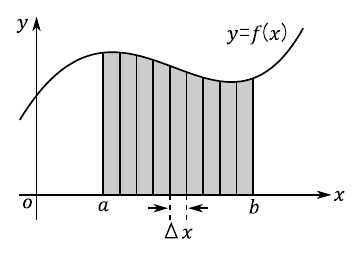
図16の色付き部分は，“$a \leqq x \leqq b$”の範囲で関数$f(x)$のグラフと$x$軸で囲まれた領域を表しています．ここでは，この領域の面積を求めることを考えます．関数$f(x)$は曲線なので，そのままでは簡単に面積を求めることができません．

ここで，「関数$f(x)$で囲まれた領域を細かく分割する」ことを考えます．分割数を“$n$”とします．また，各分割点の座標を“$x_0 = a,\ x_1,\ x_2,\ x_3,\ \cdots ,\ x_{n-1},\ x_n = b$”とし，各小区間の幅を“$\Delta x_k = x_k - x_{k-1}$”と表すことにします．さらに，分割後の$k$番目の領域において“$x_{k-1} \leqq t_k \leqq x_k$”を満たす任意の点を「代表点」“$t_k$”として定義します．

分割数“$n$”を十分に大きくすれば，各小区間を「長方形」に近似して面積を求めることができます．このとき，関数$f(x)$のグラフで囲まれた領域の面積“$S$”は，小さな長方形の面積をすべて足し合わせたものとして次のように表せます．

\begin{align} S &= f(t_1)\cdot \Delta x_1 + f(t_2)\cdot \Delta x_2 + \cdots + f(t_n)\cdot \Delta x_n \nonumber \\ &= \sum^{n}_{k=1} f(t_k) \cdot \Delta x_k \end{align}

上式のようにして曲線で囲まれた領域の面積を表したものを「リーマン和」（Riemann sum）といいます．また，この考え方は「区分求積法」と呼ばれることもあります．


図16　“$y=f(x)$”のグラフと$x$軸で囲まれた部分の面積を考える

定積分

分割数“$n$”を限りなく大きくすれば，リーマン和は対象の面積に限りなく近づくと考えられます．この「リーマン和の極限」のことを関数$f(x)$の定積分（definite integral）といい，次式で表します．

\begin{equation} \lim_{n\to \infty} \sum^{n}_{k=1} f(t_k) \cdot \Delta x_k = \int^{b}_{a} f(x) \ dx \end{equation}

上式で使われている記号“∫”は「インテグラル」（integral）といい，定積分の範囲“$a \leqq x \leqq b$”のことを「積分範囲」（interval of integral）といいます．また，定積分の計算を実行する時に値を変化させる変数（今回は“$x$”）のことを「積分変数」（variable of integration）といいます．

微積分学の基本定理

定積分の本質は「リーマン和の極限を求めること」ですが，これを手計算で実行するのは現実的に不可能です．ところが「微積分学の基本定理」（fundamental theorem of calculus）という定理を利用すると，定積分を簡単に計算できるようになります．

微積分学の基本定理は，「微分と積分は逆の演算である」という事実を示すものです．この定理があってはじめて，面積を求める「積分」と関数の傾きを求める「微分」という，一見すると何の関係も無さそうな2つの演算が結びつきます．ここでは証明を省略しますが，興味のある方は微分・積分の教科書を読んでみてください．

定積分の計算

「微積分学の基本定理」により，定積分の計算は「微分するとその関数になるものを探す」という作業に帰着します．例えば“$\cos(x)$”の積分は，先に確認した「$\sin(x)$を微分すれば$\cos(x)$になる」という事実を利用して次のように計算できます．

\begin{align} \int^{a}_{b} \cos(x) dx &= \left[ \sin(x) \right]^{b}_{a} \nonumber \\ &= \sin(b) - \sin(a) \end{align}

また“$\sin(x)$”の積分は，先に確認した「$-\cos(x)$を微分すると$\sin(x)$になる」という事実を利用して次のように計算できます．

\begin{align} \int^{a}_{b} \sin(x) dx &= \left[ -\cos(x) \right]^{b}_{a} \nonumber \\ &= -\cos(b) + \cos(a) \end{align}

不定積分

面積を求める定積分の計算とは独立して，単に「微分したらその関数になるものを求める」ことを「不定積分」（indefinite integral）といいます．定数を微分すると“0”になるので，不定積分では次のように「積分定数」（constant of integration）“$C$”を加えるのが慣例です．$\cos(x)$および$\sin(x)$の不定積分を次に示します． \begin{align} \int \cos(x)\ dx &= \sin(x) + C\\ \int \sin(x)\ dx &= -\cos(x) + C \end{align}

三角関数の積分をマイコンで計算する実験

$\cos(x)$を積分した値を求めるプログラム

マイコンを使って，本来の「リーマン和」の考え方にもとづいて関数“$f(t)=\cos(t)$”を積分してみます．なお，文字“$x$”は別のところで使いたいので，ここでは変数を“$t$”としています．

$\cos(t)$を“$t=0$”から“$t=x$”まで積分すると，次のようになります．

\begin{align} \int^{x}_{0}\cos(t)\ dt &= \left[ \sin(t) \right]^{x}_{0} \nonumber \\ &= \sin(x) - \sin(0)\nonumber \\ &= \sin(x) \end{align}

上式より，“$cos(t)$”を“$0 \leqq t \leqq x$”の範囲で積分すれば“$\sin(x)$”が得られるはずです．この計算を実行するプログラムをリスト4に示します．

  /* USER CODE BEGIN 2 */
  int i, j; //loop index
  float delta = 2*M_PI/100;
  float cos_array[100]; //sin data array
  float sum[100]; //integrated data array
  //initialize the array
  for(i=0; i<100; i++)
  {
	  cos_array[i] = cos(delta * i);
	  sum[i] = 0;
  }
  //integration
  for(i=0; i<100; i++)
  {
	  for(j=0; j<=i; j++)
	  {
		  sum[i] += cos_array[j]*delta;
	  }
  }
  //print
  for(i=0; i<100; i++)
  {
	  printf("%f\r\n", sum[i]);
  }
  /* USER CODE END 2 */





リスト4　$\cos(x)$を積分した値を出力するプログラム

`/* USER CODE BEGIN 2 / int i, j; //loop index float delta = 2M_PI/100; float cos_array[100]; //sin data array float sum[100]; //integrated data array //initialize the array for(i=0; i<100; i++) { cos_array[i] = cos(delta * i); sum[i] = 0; } //integration for(i=0; i<100; i++) { for(j=0; j<=i; j++) { sum[i] += cos_array[j]delta; } } //print for(i=0; i<100; i++) { printf("%f\r\n", sum[i]); } / USER CODE END 2 */`
リスト4　$\cos(x)$を積分した値を出力するプログラム

ソース・コードの解説

今回は$\cos(x)$の値を積分するので，最初に配列“cos_array[]”に$\cos(x)$の値を格納しています．例によって変数“delta”の値は“$2\pi/100 = 2 * \mathrm{M\_PI}/100$”としています．

“sum[]”は，$\cos(x)$を積分した結果を格納する配列です．“sum[0]”の値は“cos_array[0] * delta”となります．“sum[1]”の値は“(cos_array[0] + cos_array[1]) * delta”となります．このように，“sum[i]”の値は“cos_array[]”を0番目からi番目まですべて足し合わせて“delta”を掛け算した値になっています．これを数式で表すと，次のようになります．

\begin{equation} \mathrm{sum[i]} = \sum_{j=0}^{i} \mathrm{cos\_array[j] * delta} \end{equation}

実行結果

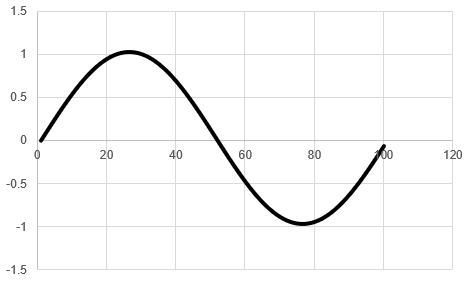
Tera Termで計算結果を受信し，Excelでグラフを描くと図17のようになります．理論どおり，「$\cos(x)$を積分すると$\sin(x)$が得られる」ことが確認できました．

なお，グラフをよく見ると最大値が1よりも大きくなっている箇所がありますが，これは数値積分の精度の問題だと考えられます．もっと分割を細かくすればより正確な値を求められますが，先にも触れた通り，いくらでも細かくすれば良いというものでもありません．十分な精度を得られる適当な分割数を探してみてください．


図17　“$f(x)=\cos(x)$”を数値的に積分した結果．理論どおり$\sin(x)$のグラフが得られる

実験しながら学ぶフーリエ解析とディジタル信号処理 [Vol.1 フーリエ解析の基本「三角関数」の正しい理解]

ディジタル信号処理の本質をマイコンで学ぶ

誰もがディジタル信号処理を活用すべき時代

計算処理を実行してこそ「コンピュータ」は真価を発揮する

ディジタル信号処理の例：高速フーリエ変換

ディジタル信号処理を学べば付加価値を上げられる

開発コストが下がったことで差別化が困難になった

演算処理が製品に価値を吹き込む

ディジタル信号処理の本質は「フーリエ解析」にある

信号処理とは「数学」である

周波数解析

フーリエ変換とラプラス変換

離散フーリエ変換とz変換

FFTとディジタル・フィルタ

フーリエ解析はあらゆる分野で核心的な役割を担っている

フーリエ解析をマイコンに実行させる

自分でディジタル信号処理を実装することを目指す

フーリエ解析の理論を体系的に理解する

コラム1 ディジタル信号処理と微分方程式

本連載で使用するSTM32系マイコンの紹介

ディジタル信号処理を学ぶための道具をそろえる

STマイクロエレクトロニクス社のマイコンと開発環境を利用する

NUCLEO-F446REボード

プログラムの作成には無償の開発環境を使う

フーリエ解析の主役である三角関数の復習

高校数学の復習から始める

三角関数の定義

サインとコサイン

タンジェント

角度の単位は「ラジアン」を使う

三角関数のグラフ

マイコンを使って正弦波のグラフを描く実験をする

プログラムを書いてコンパイルする

ソース・コードの解説

Tera Termで計算結果を受信する

Excelでグラフを描く

三角関数の加法定理

単位円上の弦“PQ”の長さを2通りの方法で表す

cosに関する加法定理

“$\theta + \pi/2$”に対する$\sin$と$\cos$の変換式

$\sin$に関する加法定理

三角関数の微分

微分の定義

$\sin(x)$を微分する

“$\sin(\Delta x)/\Delta x$”の極限

“$\left\{ \cos(\Delta x) - 1 \right\}/\Delta x$”の極限

$\sin(x)$の導関数を求める

$\cos(x)$の導関数を求める

三角関数の微分をマイコンで計算する実験

“$\sin(x)$”を微分した値を求めるプログラム

ソース・コードの解説

実行結果

三角関数の積分

リーマン和

定積分

微積分学の基本定理

定積分の計算

不定積分

三角関数の積分をマイコンで計算する実験

$\cos(x)$を積分した値を求めるプログラム

ソース・コードの解説

実行結果

実験しながら学ぶフーリエ解析とディジタル信号処理
[Vol.1　フーリエ解析の基本「三角関数」の正しい理解]

コラム1　ディジタル信号処理と微分方程式