【Digi-Key社提供】フレッシャーズ＆学生応援特別企画
実験しながら学ぶフーリエ解析とディジタル信号処理
[Vol.3 「フーリエ級数」を利用して波形を合成する実験]
スペクトル解析やディジタル・フィルタを最適化してマイコンに実装
- 著者・講師：別府 伸耕/Nobuyasu Beppu (リニア・テック)
- 企画編集・主催： ZEPエンジニアリング株式会社
- 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
- 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
- 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
- 関連製品：［VOD/KIT］STM32マイコン＆Wi-Fiモジュールで学ぶ C/C++プログラミング入門
- 関連記事：Pythonではじめる 数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
- 関連記事：Pythonではじめる 数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]
【Index】
三角関数を組み合わせて矩形波を作る実験
信号処理を“NUCLEO”マイコン・ボードで実験しながら学ぶ
|
|---|
| 写真1 本連載で扱う内容はすべて“NUCLEO-F446RE”ボード(STマイクロエレクトロニクス)で実験できる |
本連載では，32ビットARM Cortex-M4コアを搭載したワンチップ・マイコンである“STM32F446”で実際に信号処理を行いながら，ディジタル信号処理の核心を担う理論である「フーリエ解析」を学びます．
実験に必要なのは“STM32F446”の評価ボードである“NUCLEO-F446RE”（2,000円程度）とUSBケーブルだけです．ぜひ自分の手でプログラムを書いて実験しながら記事を読み進めてみてください．
分析対象のデータは何らかの「関数」として表現できる
これから学ぶ「フーリエ解析」や「ディジタル信号処理」は，様々なデータを加工して有益な情報を引き出すための技術です．分析の対象はマイクに入力された音声信号やカメラでとらえた画素データ，さらには人口や株価の変化，地域ごとの降水量や川の水深データに至るまで，幅広い分野のデータを扱うことができます．
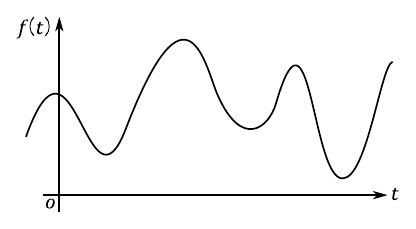
これから行う信号処理の対象は，図1のような「時間的に変化する波形」として表されるデータであるとします．このような波形は，一般的に時間“$t$”の関数“$f(t)$”として表現できます．我々がオシロスコープで測定した波形や，データ・ロガーで取得した測定データなどがこれに該当します．
|
|---|
| 図1 分析の対象となるデータの波形は，何らかの「関数」として表される |
時間的に変化しないデータであっても構わない
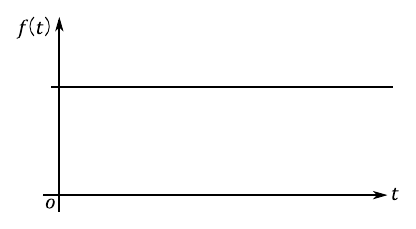
信号処理の対象として，図2のような「時間的に変化しないデータ」を選んでも構いません．これは，「時間的に変化するデータ」の特別な場合（すべての時刻において同じ値をとる場合）であると考えられます．ただし，時間的に変化しないデータを出力するような対象はその素性がわかりきっているので（一定値のまま変化しないから），わざわざ「分析」を行う必要がない場合がほとんどです．
|
|---|
| 図2 時間的に変化しないデータを扱ってもよいが，「分析」をするまでもない場合がほとんどである |
空間的な値の分布に対して分析を行うこともできる
時間的に変化するデータではなく，空間的に変化する対象を扱いたい場合もあるかと思います．例えば，「場所ごとにことなる温度分布の測定データ」などが挙げられます．このような場合は分析対象のデータを位置“$x$”の関数“$f(x)$”として表現することで，時間的に変化する信号を扱うときと全く同様の手法を利用することができます．いずれにしても，分析対象のデータを何らかの「関数」として取り扱うことが重要となります．
ここから先は数学的に一般化した議論を扱いたいので，いったん「位置」“$x$”や「時間」“$t$”といった物理的なイメージから離れることにします．特別な場合を除いて変数はすべて“$x$”とし，分析対象となる関数は“$f(x)$”と表記することにします．
数学者フーリエが考えたこと
一般的に，分析対象のデータは不規則かつ複雑な波形になりがちです．どんな波形にも対応できる「汎用的かつ統一的な分析手法」があれば便利ですが，それを生み出すのは非常に困難でしょう．ところが，この問題を解決する驚くべきアイディアがフランスの数学者ジョゼフ・フーリエ（Joseph Fourier, 1768 - 1830）によって出されました．
フーリエが提唱したのは，汎用的な信号処理に応用できる非常に重要な考え方です．それは，「あらゆる周期関数は様々な三角関数の和によって表せる」というアイディアでした．例えば，「何らかの関数“$f(x)$”を$\sin$関数の足し合わせで表す」という操作は式(1)のように表せます．
\begin{equation} \label{eq:fourier_idea} f(x) = a_{1}\cdot \sin(x) + a_{2}\cdot \sin(2x) + a_{3}\cdot \sin(3x) + \cdots \end{equation}式(1)では“$\sin(x),\ \sin(2x),\ \sin(3x),\ \cdots$”といった様々な周期の$\sin$関数を足し合わせています．“$a_{1},\ a_{2},\ a_{3},\ \cdots$”は，それぞれの周期をもつ成分の振幅（全体に対する寄与率）を調整するための定数です．なお，ここでは$\sin$関数だけを使った例を示していますが，実際は$\sin$と$\cos$の両方を組み合わせて使うのが一般的です．フーリエの理論は，式(1)のような形で「どんな周期関数$f(x)$でも表現できる」という話から出発します．
sin関数だけで矩形波を作る実験
式(1)のような形で様々な関数を表現できるという事実は，初めてフーリエ解析を学ぶ人にとっては信じがたいことかもしれません．そこで，簡単な実験を行って「三角関数の重ね合わせ」の威力を実感してみることにします．
|
|---|
| 図3 このような波形を「矩形波」という．矩形波はsin関数の足し合わせによって作れる |
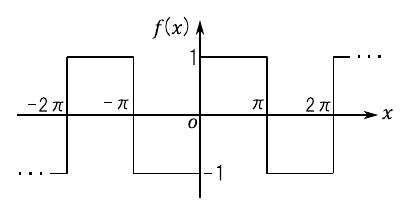
ここでは，$\sin$関数だけを使って図3のような「矩形波」（くけいは，square wave）を作ってみます．我々が知っている$\sin$関数のグラフはなめらかな曲線であり，カクカクとした図3の矩形波とはまったく異なる形をしています．ところが，式(2)にもとづいて計算を行うと関数“$f(x)$”として図3の矩形波を得ることができます．
\begin{align} \label{eq:square_wave_example} f(x) &= \cfrac{4}{\pi} \cdot \sum^{\infty}_{k=0} \cfrac{1}{2k+1} \cdot \sin \left\{ (2k+1) x \right\} \nonumber \\ &= \cfrac{4}{\pi} \cdot \left\{ \sin(x) + \cfrac{1}{3} \cdot \sin(3x) + \cfrac{1}{5} \cdot \sin(5x) + \cfrac{1}{7}\cdot \sin(7x) + \cdots \right\} \end{align}式(2)を導く具体的な方法は，これからフーリエ解析を学びながら解説します．ここでは，とりいそぎ式(2)を利用して本当に$\sin$関数の重ね合わせによって矩形波を作れるのかを確かめてみることにします．
sin関数を組み合わせて矩形波を作るプログラムのソース・コード
今回も，例によって“NUCLEO-F446RE”ボードを使って実験を行います．本連載のVol. 2で紹介した手順にしたがい，新しいプロジェクトを作成してクロックやUARTなどの設定を行ってください．また，“stdio.h”や“math.h”をインクルードしたり“printf()”関数を使うための準備を済ませたりしておいてください．
開発環境上で“main.c”のソース・コードを開き，“/* USER CODE BEGIN 0 */”と“/* USER CODE END 0 */”の間の部分にリスト1に示す関数“square_wave()”を記述してください（printf()関数を使うために記述している_write()関数の下に追記する形になる）．
この関数“square_wave()”では，式(2)の計算をそのまま行って結果を配列“data_array[]”に格納しています．変数“N”は足し合わせる$\sin$関数の項数を表します．理想的には“$\textrm{N}=\infty$”とすべきですが，コンピュータ上で無限回の計算を実行するのは難しいので“N”はできるだけ大きい値として設定するようにします．変数“delta”は波形を計算する際の1ステップあたりの刻み幅です．今回は適当な値として“$\mathrm{delta} = 2\pi / 100$”としました．19行目の部分が，式(2)の計算に相当します．最後に27行目から30行目の部分で計算結果をUART経由で出力しています．
|
|---|
| リスト1 矩形波を出力する関数“square_wave()” |
main()関数の内部では，リスト2に示すように“/* USER CODE BEGIN 2 */”から“/* USER CODE END 2 */”の間の部分に関数“square_wave()”を呼び出す処理を記述しておきます．
|
|---|
| リスト2 矩形波を出力するプログラムのmain()関数内部の記述 |
実験結果
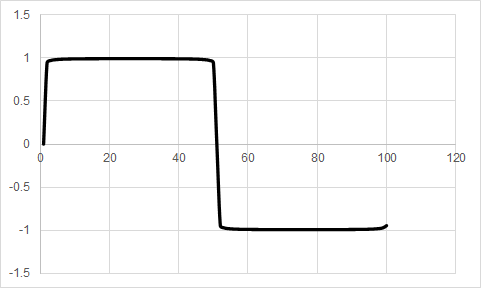
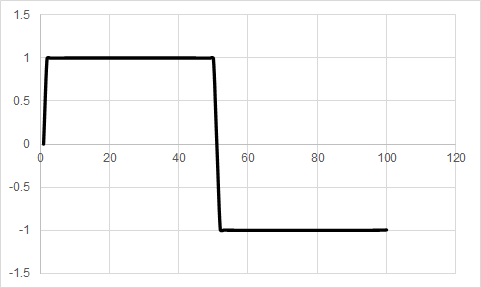
本連載のVol. 2で紹介した方法にしたがって，ソース・コードをコンパイルしてプログラムをマイコンに書き込んでください．“Tera Term”を起動してから“NUCLEO-F446RE”ボードのリセット・スイッチ（黒色）を押すと，マイコンがUART経由で出力した計算結果がTera Term上に表示されます．この計算結果をExcelにコピーしてグラフを描いたものが，図4から図9に示す波形です．
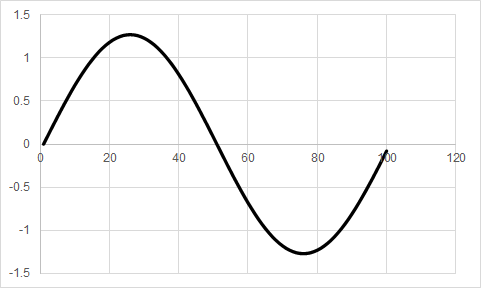
図4はリスト1において“N=1”とした場合に得られるグラフです．これは“$f(x)=4/\pi \cdot \sin(x)$”のグラフそのものです．
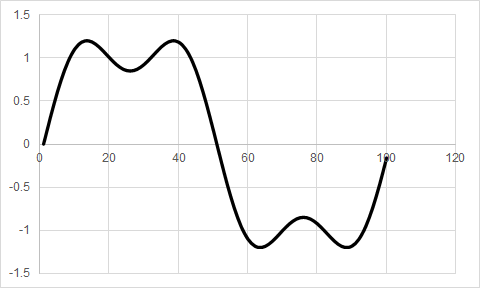
図5は“N=2”とした場合のグラフです．これは“$f(x)=4/\pi \cdot \left\{ \sin(x) + \sin(3x)/3 \right\}$”のグラフに相当します．もともとの“$\sin(x)$”のグラフの山の部分（$\sin(x)$の$x=\pi/2$の部分に相当）が“$\sin(3x)$”のグラフの谷の部分と重なることで，いくらか平坦化されていることがわかります．谷の部分（$\sin(x)$の$x=3\pi/2$の部分に相当）も同様にピークが打ち消されています．
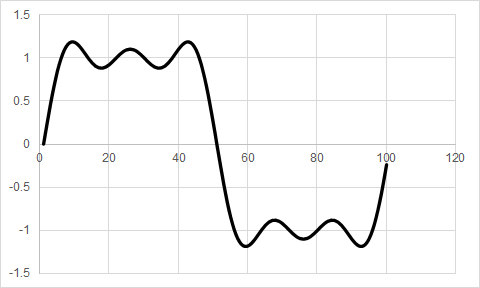
図6は“N=3”とした場合のグラフです．これは“$f(x)=4/\pi \cdot \left\{ \sin(x) + \sin(3x)/3 + \sin(5x)/5 \right\}$”のグラフに相当します．また，図7は“N=10”とした場合のグラフです．これは10個の$\sin$関数を足し合わせた波形で，“$f(x)=4/\pi \cdot \left\{ \sin(x) + \sin(3x)/3 + \cdots + \sin(19x)/19 \right\}$”のグラフに相当します．かなり矩形波に近くなってきました．
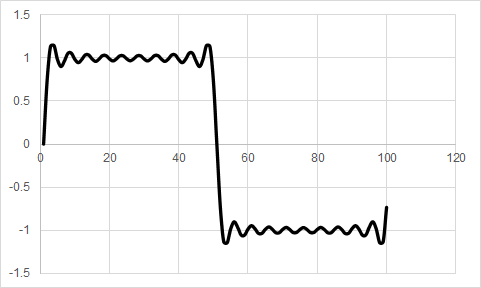
図8は“N=100”とした場合，図9は“N=1000”とした場合のグラフです．ここまでくると，ほとんど矩形波であると言ってもよいでしょう．なお，“N=100”の場合のマイコンの計算時間はおよそ2秒ほどです．また，“N=1000”の場合は計算に20秒ほどかかります．自分でリスト1の変数“N”の値をいろいろと変更して，計算結果のグラフの形や計算時間の変化を確かめてみてください．
|
|
|---|---|
| 図4 N=1のときの波形 | 図5 N=2のときの波形 |
|
|
| 図6 N=3のときの波形 | 図7 N=10のときの波形 |
|
|
| 図6 N=100のときの波形 | 図7 N=1000のときの波形 |
どんな波形でも三角関数の重ね合わせで作れるのか？
以上の実験から，たしかに「$\sin$関数を組み合わせると矩形波を作れる」ことがわかりました．この他にも「三角波」や「のこぎり波」など様々な波形を三角関数の組み合わせによって作れることが知られています．
すると，「ありとあらゆる波形を三角関数の組み合わせで表現できるのか？」という疑問が生じるかと思います．ここでは数学的に厳密な議論は省略しますが，少なくとも我々がオシロスコープで測定するような波形はすべて対応することができます．もし厳密な内容に興味がある場合は，「フーリエ級数の収束」というキーワードで調べてみてください．
なお，三角関数は「周期関数」なので，三角関数によって表現できる波形も周期関数に限られます．ただし，三角関数の組み合わせで表現する波形の周期を「1万年」など非常に長い時間に設定すれば，人間の時間感覚としては「測定期間内に1回しか現れない波形」を扱うことができます．そのため，「周期関数しか表現できない」という制限は実用上あまり問題になりません．
関数は「ベクトル」である
ベクトル
ここでは，フーリエ解析と非常に深い関わりがある「ベクトル」の基本事項を復習しておきます．これまでの「三角関数を使えばいろいろな波形を表せる」という話題から外れているように思われるかもしれませんが，ベクトルはフーリエ解析の根幹を担っています．少しばかりお付き合いいただければと思います．
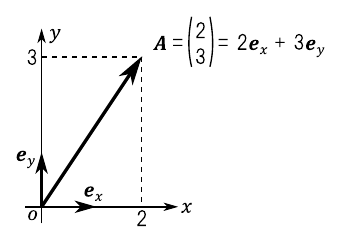
\begin{equation} \bm{A} = \left( \begin{array}{c} 2 \\ 3 \\ \end{array} \right) \end{equation}上式の“$\bm{A}$”のように，複数の数字を括弧でくくってまとめたものを「ベクトル」（vector）といいます．ベクトルは一般的に太字で表記します．上式における“2”や“3”のように，ベクトルに含まれる要素のことを「成分」（component）といいます．また，ベクトルに含まれる成分の数のことを「次元」（dimension）といいます．上式のベクトル“$\bm{A}$”は「2次元」であり，2次元のベクトルは図10のように「2次元平面内の矢印」としてイメージすることができます．
|
|---|
| 図10 複数の数字をひとつにまとめたものを「ベクトル」と呼ぶ．2次元のベクトルは平面上の矢印としてイメージできる |
ベクトル$\bm{A}$の長さ（絶対値）を“$|\bm{A}|$”と表記します．図10において「三平方の定理」を適用すると，“$|\bm{A}|$”は次のように求められます．
\begin{equation} |\bm{A}| = \sqrt{2^{2} + 3^{2}} = \sqrt{13} \end{equation}なお，長さが“1”のベクトルは「単位ベクトル」（unit vector）と呼ばれます．
基底ベクトル
図11に示すように，$x$軸方向を向いた単位ベクトル“$\bm{e}_{x}$”と，$y$軸方向を向いた単位ベクトル“$\bm{e}_{y}$”を用意します．
\begin{equation} \bm{e}_{x} = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) , \ \ \ \bm{e}_{y} = \left( \begin{array}{c} 0 \\ 1 \end{array} \right) \end{equation}これらのベクトル“$\bm{e}_{x}$”および“$\bm{e}_{y}$”を利用すると，さきほど考えたベクトル“$\bm{A}$”は次のように表せます．
\begin{align} \bm{A} &= \left( \begin{array}{c} 2 \\ 3 \end{array} \right) \nonumber \\ &= 2 \cdot \left( \begin{array}{c} 1 \\ 0 \end{array} \right) + 3 \cdot \left( \begin{array}{c} 0 \\ 1 \end{array} \right) \nonumber \\ &= 2 \cdot \bm{e}_{x} + 3 \cdot \bm{e}_{y} \end{align}上式と同様に考えると，第一成分が“$A_{x}$”で第二成分が“$A_{y}$”である任意のベクトル“$\bm{A}$”は次のように表せます．
\begin{equation} \bm{A} = \left( \begin{array}{c} A_{x} \\ A_{y} \end{array} \right) = A_{x} \cdot \bm{e}_{x} + A_{y} \cdot \bm{e}_{y} \end{equation}上式は，「“$\bm{e}_{x}$”と“$\bm{e}_{y}$”をそれぞれ適当に伸び縮みさせて足し合わせれば，2次元平面内のあらゆるベクトルを表現できる」ということを意味しています．このようなベクトル“$\bm{e}_{x}$”，“$\bm{e}_{y}$”のことを2次元の「基底」（basis）あるいは「基底ベクトル」（basis vector）といいます．
|
|---|
| 図11 2次元平面内のすべてのベクトルは，基底ベクトル“$\bm{e}_{x}$”および“$\bm{e}_{y}$”の組み合わせで表現できる |
基底ベクトルのとり方は何通りも考えられます．2次元平面内のベクトルを一意に表現できるならば，どのようなベクトルを基底として使っても構いません．なお，図11の“$\bm{e}_{x}$”および“$\bm{e}_{y}$”は長さが“1”で互いに直交しているので，「正規直交基底」（orthonormal basis）という特別な呼び名があります．
今回は2次元ベクトルの例で考えましたが，3次元ベクトルを扱う場合は3つの基底ベクトルが必要になります．例えば$x$，$y$，$z$軸方向を向いた単位ベクトル$\bm{e}_{x}$，$\bm{e}_{y}$，$\bm{e}_{z}$を基底として（これは3次元の正規直交基底だと言える）一般の3次元ベクトル“$\bm{A}$”を表現すると式(8)のようになります．ただし“$A_{x}$”，“$A_{y}$”，“$A_{z}$”は3次元ベクトル“$\bm{A}$”の各成分です．
\begin{equation} \label{eq:vector_3d_example1} \bm{A} = A_{x} \cdot \bm{e}_{x} + A_{y} \cdot \bm{e}_{y} + A_{z} \cdot \bm{e}_{z} \end{equation}一般の$n$次元ベクトルを表現するには，$n$個の基底が必要となります．$n$個の基底を“$\bm{e}_{1}$”，“$\bm{e}_{2}$”，$\cdots$，“$\bm{e}_{n}$”とすると，次のような具合になります．
\begin{equation} \label{eq:vector_nd_example1} \bm{A} = A_{1} \cdot \bm{e}_{1} + A_{2} \cdot \bm{e}_{2} + \cdots + A_{n} \cdot \bm{e}_{n} \end{equation}ベクトルの内積
ここでは，「ベクトルどうしの演算」について考えることにします．ベクトルどうしの演算には「足し算」，「引き算」，「掛け算」がありますが，足し算と引き算はベクトルの各成分どうしの足し算あるいは引き算を行うだけなので解説は省略します．ベクトルどうしの「掛け算」には，「内積」（inner product）と「外積」（cross product）の2種類があります．このうち，フーリエ解析でよく使うのは「内積」のほうです．
|
|---|
| 図12 ベクトルの内積の定義 |
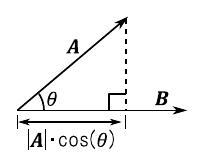
図12のように，2つのベクトル“$\bm{A}$”および“$\bm{B}$”を考えます．これらのベクトルがなす角度を“$\theta$”としたとき，$\bm{A}$と$\bm{B}$の内積“$\bm{A} \cdot \bm{B}$”は次のように定義されます．
\begin{equation} \bm{A} \cdot \bm{B} = |\bm{A}| \cdot |\bm{B}| \cdot \cos(\theta) \end{equation}内積の定義式における“$|\bm{A}|\cdot \cos(\theta)$”の部分は，ベクトル$\bm{A}$のうちベクトル$\bm{B}$と同じ方向の成分の大きさを表しています．もしベクトル$\bm{A}$と$\bm{B}$が同じ方向を向いていて“$\theta = 0$”となる場合，内積“$\bm{A}\cdot\bm{B}$”の値は最大値“$|\bm{A}|\cdot|\bm{B}|$”となります．
\begin{align} \bm{A} \cdot \bm{B} &= |\bm{A}| \cdot |\bm{B}| \cdot \cos(0) \nonumber \\ &= |\bm{A}| \cdot |\bm{B}| \end{align}一方で，ベクトル$\bm{A}$と$\bm{B}$が互いに逆の方向を向いていて“$\theta = \pi$”となる場合，内積“$\bm{A}\cdot\bm{B}$”の値は最小値“$-|\bm{A}|\cdot|\bm{B}|$”となります．
\begin{align} \bm{A} \cdot \bm{B} &= |\bm{A}| \cdot |\bm{B}| \cdot \cos(\pi) \nonumber \\ &= -|\bm{A}| \cdot |\bm{B}| \end{align}もしベクトル$\bm{A}$と$\bm{B}$が互いに直交する場合は“$\theta = \pi/2$”となるので，内積“$\bm{A}\cdot\bm{B}$”の値は“0”になります．
\begin{align} \bm{A} \cdot \bm{B} &= |\bm{A}| \cdot |\bm{B}| \cdot \cos(\pi/2) \nonumber \\ &= 0 \end{align}以上のことから，内積とは「2つのベクトルがどれだけ同じ成分を持つか」を表す指標であると考えられます．特に，内積が“0”になるときは「2つのベクトルが共通した要素をまったく持たない」という意味で，「直交している」（orthogonal）という言い方をします．
ベクトルの内積を成分計算で表す
さきほど確認したベクトルの内積の定義は，ベクトルの「長さ」や「角度」など図形的なパラメータを使ったものでした．ここではベクトルの「成分」を使って内積を計算する方法を確認します．以下，ベクトル“$\bm{A}$”および“$\bm{B}$”の成分を次式のように定めます．
\begin{equation} \bm{A} = \left( \begin{array}{c} A_{x} \\ A_{y} \end{array} \right) , \ \ \ \bm{B} = \left( \begin{array}{c} B_{x} \\ B_{y} \end{array} \right) \end{equation}上式の定義を使うと，ベクトルの絶対値“$|\bm{A}|$”および“$|\bm{B}|$”は次のように表せます．
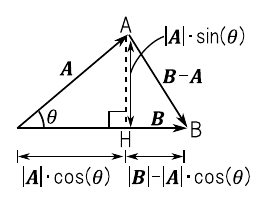
\begin{equation} |\bm{A}|=\sqrt{{A_{x}}^{2} + {A_{y}}^{2}} , \ \ \ |\bm{B}|=\sqrt{{B_{x}}^{2} + {B_{y}}^{2}} \end{equation}また，図13のベクトル“$|\bm{B}-\bm{A}|$”の長さは次のように表せます．
\begin{equation} |\bm{B}-\bm{A}| = \sqrt{{(B_x - A_x)}^2 + {(B_y - A_y)}^2 } \end{equation}
|
|---|
| 図13 三角形ABHで三平方の定理を使う |
ここで，図13のように点Aからベクトル$\bm{B}$に対して垂線をおろし，その交点を“H”とします．三角形ABHに対して「三平方の定理」を適用すると次のようになります．なお，この式は「余弦定理」とも呼ばれます．
\begin{align} |\bm{B}-\bm{A}|^2 &= \left\{ |\bm{A}|\cdot \sin(\theta) \right\}^2 + \left\{ |\bm{B}|-|\bm{A}|\cdot \cos(\theta) \right\}^2 \nonumber \\ &= |\bm{A}|^2 \cdot \sin^{2}(\theta) + \left\{ |\bm{B}|^2 - 2\cdot |\bm{A}|\cdot|\bm{B}|\cdot \cos(\theta) + |\bm{A}|^2 \cdot \cos^{2}(\theta) \right\} \nonumber \\ &= |\bm{A}|^2 + |\bm{B}|^2 - 2\cdot|\bm{A}|\cdot|\bm{B}|\cdot \cos(\theta) \end{align}上式を利用すると，“$\cos(\theta)$”は次のように表せます．
\begin{align} \cos(\theta) &= \cfrac{|\bm{A}|^2 + |\bm{B}|^2 - |\bm{B}-\bm{A}|^2}{2\cdot|\bm{A}|\cdot|\bm{B}|} \end{align}上式の“$\cos(\theta)$”を利用すると，ベクトルの内積“$\bm{A}\cdot\bm{B}$”は次のように表せます．
\begin{align} \bm{A}\cdot\bm{B} &= |\bm{A}|\cdot |\bm{B}| \cdot \cos(\theta) \nonumber \\ &= |\bm{A}| \cdot |\bm{B}| \cdot \cfrac{|\bm{A}|^2 + |\bm{B}|^2 - |\bm{B}-\bm{A}|^2}{2\cdot|\bm{A}|\cdot|\bm{B}|} \nonumber \\ &= \cfrac{1}{2} \cdot ( |\bm{A}|^2 + |\bm{B}|^2 - |\bm{B}-\bm{A}|^2 ) \nonumber \\ &= \cfrac{1}{2} \cdot \left[ ({A_{x}}^2 + {A_{y}}^2) + ({B_{x}}^2 + {B_{y}}^2) - \left\{ (B_x - A_x)^2 + (B_y - A_y)^2 \right\} \right] \nonumber \\ &= A_x \cdot B_x + A_y \cdot B_y \end{align}結局のところ，ベクトルの内積を計算するには「2つのベクトルの各成分を掛け算して，すべて足し合わせればよい」ことがわかりました．この結果は，2次元ベクトルに限らず一般の$n$次元ベクトルにも一般化できます．例えば，次のように$n$次元のベクトル$\bm{A}$および$\bm{B}$があったとします．
\begin{equation} \bm{A} = \left( \begin{array}{c} A_1 \\ A_2 \\ \vdots \\ A_n \end{array} \right) , \ \ \ \bm{B} = \left( \begin{array}{c} B_1 \\ B_2 \\ \vdots \\ B_n \end{array} \right) \end{equation}このとき，2つのベクトルの内積“$\bm{A}\cdot\bm{B}$”は次のように計算できます．
\begin{equation} \bm{A}\cdot\bm{B} = A_1 \cdot B_1 + A_2 \cdot B_2 + \cdots + A_n \cdot B_n \end{equation}人間の感覚では，「$n$次元のベクトル」というものを図形的にイメージするのは難しいかもしれません．それでも，「内積」という計算の性質を考えれば，上式で表される内積“$\bm{A}\cdot\bm{B}$”は「ベクトル$\bm{A}$と$\bm{B}$の共通成分の大きさ」に相当するものであると理解できます．
関数は「無限次元のベクトル」だと見なせる
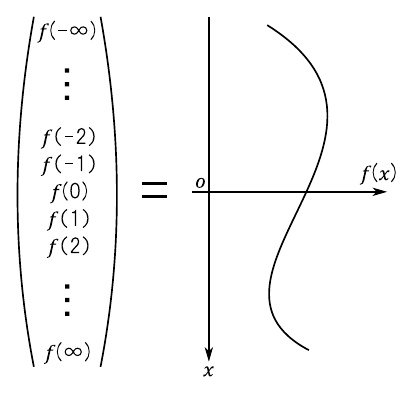
データの「波形」，すなわち「関数」の話題に戻ります．今後は特に断らない限り，関数“$f(x)$”は“$x=-\infty$”から“$x=\infty$”の範囲で定義されているものとします．
ここで，何らかの関数“$f(x)$”のグラフを図14のように$90^{\circ}$回転させて眺めてみます．関数$f(x)$は$x=-\infty$，$\cdots$，$x=-2$，$x=-1$，$x=0$，$x=1$，$x=2$，$\cdots$，$x=\infty$といった各点において，$f(-\infty)$，$\cdots$，$f(-2)$，$f(-1)$，$f(0)$，$f(1)$，$f(2)$，$\cdots$，$f(\infty)$という値をとります．なお，ここでは簡単のために$x$の値を整数で書いていますが，本来$x$はもっと細かい値（実数全体）をとります．
|
|---|
| 図14 関数は「無限次元のベクトル」であると見なせる |
このようにして見ると，図14の関数$f(x)$のグラフは「様々な$x$の値に対応する$f(x)$の値をまとめたもの」になっています．「複数の値を1つに束ねたもの」であることから，「関数はベクトルである」と考えることができます．図14では関数$f(x)$は$f(-\infty)$から$f(\infty)$までの無限個の点から構成されているので，この関数$f(x)$は「無限次元のベクトル」ということになります．
なお，我々がオシロスコープで測定する波形やデータ・ロガーで取得する測定データなどは高々有限個の値しか持ちません．もしオシロスコープで測定した波形のサンプリング点数が1024ポイントならば，その波形は「1024次元のベクトル」ということになります．このように「関数をベクトルとして扱う」という感覚は，これからフーリエ解析を学ぶ上で非常に重要となります．
関数どうしの内積
関数を「ベクトル」として扱えるならば，ベクトルに対して定義されている「内積」という計算を関数に対しても実行できるはずです．そこで，ここでは「関数どうしの内積」について考えてみることにします．
$x=-\infty$から$x=\infty$までの領域で定義されている関数“$f(x)$”および“$g(x)$”があったとします．これらの関数を「無限次元のベクトル」として見なした場合，これらの関数の「内積」“$(f,g)$”は次のように計算できると考えられます．
\begin{equation} (f, g) = f(-\infty)\cdot g(-\infty) + \cdots + f(0) \cdot g(0) + \cdots + f(\infty) \cdot g(\infty) \end{equation}上式は，あくまで「ベクトルの内積」をもとにして直感的に考えた式です．実際の$f(x)$や$g(x)$は$x=-\infty$から$x=\infty$まで無限に細かい値をとるので，次のように積分の形で表現したほうが適切であると考えられます．よって，今後は次式を「関数$f(x)$と関数$g(x)$の内積“$(f,g)$”を求める式」として使うことにします．
\begin{equation} (f,g) = \int^{\infty}_{-\infty} f(x) \cdot g(x) dx \end{equation}上式の計算結果が大きいほど，「関数$f(x)$と$g(x)$はよく似ている」と考えられます． また，上式の値が“0”になったときは「関数$f(x)$と$g(x)$の間に共通成分はない」すなわち「関数$f(x)$と$g(x)$は直交している」ということになります．このような事情により，上式の計算によって得られる値は関数$f(x)$と$g(x)$の「相関」（correlation）と呼ばれることがあります．
三角関数の直交性
三角関数は様々な関数の「基底」になっている
任意の2次元ベクトルは，2つの基底“$\bm{e}_{x}$”と“$\bm{e}_{y}$”を組み合わせることで表現できます．また同様に，任意の$n$次元ベクトルは$n$個の基底“$\bm{e}_{1}$”，“$\bm{e}_{2}$”，$\cdots$，“$\bm{e}_{n}$”によって表現できます．ここで，さきほどの「関数はベクトルである」という話をあわせると，「関数にも基底ベクトルに相当するものがあるのではないか？」という発想が生まれます．
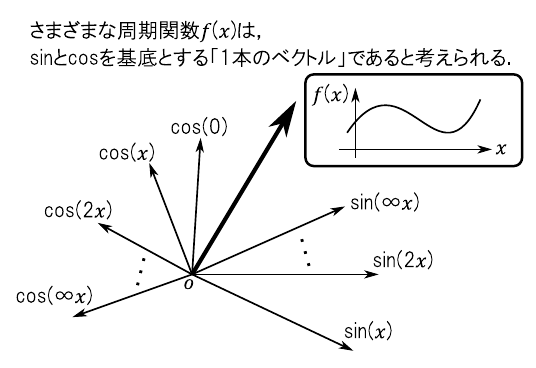
先に実験で確認したとおり，「$\sin$関数を組み合わせれば矩形波を作れる」のでした．矩形波に限らず，いろいろな周期の$\sin$関数と$\cos$関数を組み合わせれば様々な周期関数を作ることができます．このことから，「三角関数は様々な関数の基底になっている」と考えられます．
このイメージを図15に示します．この空間は無限個の$\sin$および$\cos$によって作られる「無限次元空間」なので，図として正確に描くことは困難です．あくまでイメージとして理解してください．“$\sin(x)$”,“$\sin(2x)$”，$\cdots$という無限個の関数がこの空間の基底です．周期関数$f(x)$は，これらの基底を適当に組み合わせて作った「1本のベクトル」に相当します．このように考えれば，「$\sin$関数を組み合わせて矩形波を作れる」という事実もいくらか納得できるのではないでしょうか．
|
|---|
| 図15 三角関数はあらゆる周期関数の「基底」になっていると考えられる |
信号処理でよく使う「フーリエ変換」の本質
ここまで考えてきた「$\sin$と$\cos$は様々な周期関数の基底である」という話は，これから学ぶフーリエ解析という分野の本質です．$\sin$や$\cos$を適当に「ブレンド」することで好きな形の波形を構築できるならば，次は「いま測定したこの波形には$\sin$や$\cos$がどれくらいの割合で含まれているのか？」ということが知りたくなります．後で解説する「フーリエ変換」という演算は，まさにこの「含有量」を求めるための計算処理です．
フーリエ変換によって各周期の$\sin$や$\cos$の「含有量」がわかれば，その値にしたがって$\sin$や$\cos$を混ぜ合わせることで好きな波形を再現できるはずです．この演算は，「逆フーリエ変換」と呼ばれます．いずれにしても，すべての根底にあるのは「関数をベクトルとして見なしたとき，その基底は$\sin$と$\cos$である」という考え方です．
「フーリエ変換」については，もう少し数学的な準備を整えてから詳しく解説することにします．
周期が異なる$\sin$関数どうしは直交している
先に例として考えた2次元ベクトルの基底“$\bm{e}_{x}$”と“$\bm{e}_{y}$”は，それぞれ$x$軸方向と$y$軸方向を向いているので明らかに「直交」しています．実際に内積を計算してみると，次のように“0”になることが確認できます．
\begin{align} \bm{e}_{x} \cdot \bm{e}_{y} &= \left( \begin{array}{c} 1 \\ 0 \end{array}\right) \cdot \left( \begin{array}{c} 0 \\ 1 \end{array}\right) \nonumber \\ &= 1\cdot 0 + 0 \cdot 1 \nonumber \\ &= 0 \end{align}それでは，「関数の基底」である$\sin$関数や$\cos$関数は互いに直交しているのでしょうか．基底は必ずしも直交している必要はありませんが，直交していれば「互いにまったく共通成分を持たない基底」すなわち「無駄のない基底」であると言えます．これを確かめるために，$\sin$や$\cos$について「関数どうしの内積」を計算してみましょう．
まずは，$\sin$関数どうしが直交していることを確認します．ここでは一般化して，“$\sin(mx)$”と“$\sin(nx)$”の内積を求めてみます．“$m$”および“$n$”は自然数とします（$\sin$関数の周期はそれぞれ“$2\pi/m$”および“$2\pi/n$”となる）．また，積分範囲は“$-\infty < x < \infty$”ではなく三角関数の基本周期である$0 \leqq x \leqq 2\pi$の範囲とします．
\begin{align} \left( \sin(mx),\ \sin(nx) \right) &= \int^{2\pi}_{0} \sin(mx)\cdot\sin(nx) dx \nonumber \\ &= \int^{2\pi}_{0} \cfrac{\cos\left\{(m-n)x\right\} - \cos\left\{(m+n)x\right\}}{2} dx \end{align}上式の変形では，いわゆる「積和公式」（$\cos$の「加法定理」をもとにして導出できる）を使いました．ここで，“$m=n$”の場合は上式の計算結果は次のようになります．
\begin{align} &\cfrac{1}{2} \cdot \int^{2\pi}_{0} 1- \cos\left\{(m+n)x\right\} dx \nonumber \\ =& \cfrac{1}{2} \cdot \left[ x - \cfrac{1}{(m+n)} \cdot \sin\left\{(m+n)x\right\} \right]^{2\pi}_{0} \nonumber \\ =& \ \pi \end{align}また，“$m \neq n$”の場合は次のようになります．
\begin{align} &\cfrac{1}{2} \cdot \int^{2\pi}_{0} \cos\left\{(m-n)x\right\} - \cos\left\{(m+n)x\right\} dx \nonumber \\ =& \cfrac{1}{2} \cdot \left[ \cfrac{1}{m-n}\cdot \sin\left\{(m-n)x\right\} - \cfrac{1}{(m+n)} \cdot \sin\left\{(m+n)x\right\} \right]^{2\pi}_{0} \nonumber \\ =& \ 0 \end{align}結局，内積“$(\sin(mx),\ \sin(nx))$”の計算結果は次のようにまとめられます．
\begin{eqnarray} (\sin(mx),\ \sin(nx)) = \left\{ \begin{array}{ll} \pi & (m = n) \\ 0 & (m \neq n)\\ \end{array} \right. \end{eqnarray}以上のことから，「周期が異なる$\sin$関数どうしはすべて直交している」ことがわかりました．
周期が異なる$\cos$関数どうしは直交している
$\cos$関数どうしの直交性についても調べてみましょう．次のように，$\cos(mx)$と$\cos(nx)$の内積“$(\cos(mx),\ \cos(nx))$”を計算します．
\begin{align} \left( \cos(mx),\ \cos(nx) \right) &= \int^{2\pi}_{0} \cos(mx)\cdot\cos(nx) dx \nonumber \\ &= \int^{2\pi}_{0} \cfrac{\cos\left\{(m-n)x\right\} + \cos\left\{(m+n)x\right\}}{2} dx \end{align}ここで，“$m=n$”の場合は上式の計算結果は次のようになります．
\begin{align} &\cfrac{1}{2} \cdot \int^{2\pi}_{0} 1 + \cos\left\{(m+n)x\right\} dx \nonumber \\ =& \cfrac{1}{2} \cdot \left[ x + \cfrac{1}{(m+n)} \cdot \sin\left\{(m+n)x\right\} \right]^{2\pi}_{0} \nonumber \\ =& \ \pi \end{align}また，“$m \neq n$”の場合は次のようになります．
\begin{align} &\cfrac{1}{2} \cdot \int^{2\pi}_{0} \cos\left\{(m-n)x\right\} + \cos\left\{(m+n)x\right\} dx \nonumber \\ =& \cfrac{1}{2} \cdot \left[ \cfrac{1}{m-n}\cdot \sin\left\{(m-n)x\right\} + \cfrac{1}{(m+n)} \cdot \sin\left\{(m+n)x\right\} \right]^{2\pi}_{0} \nonumber \\ =& \ 0 \end{align}結局，内積“$(\cos(mx),\ \cos(nx))$”の計算結果は次のようにまとめられます．
\begin{eqnarray} (\cos(mx),\ \cos(nx)) = \left\{ \begin{array}{ll} \pi & (m = n) \\ 0 & (m \neq n)\\ \end{array} \right. \end{eqnarray}以上のことから，「周期が異なる$\cos$関数どうしはすべて直交している」ことがわかりました．
$\sin$関数と$\cos$関数は直交している
$\sin$関数と$\cos$関数が互いに直交していることも確認しておきましょう．次のように，内積“$(\sin(mx),\ \cos(nx))$”を計算します．
\begin{align} \left( \sin(mx),\ \cos(nx) \right) &= \int^{2\pi}_{0} \sin(mx)\cdot\cos(nx) dx \nonumber \\ &= \int^{2\pi}_{0} \cfrac{\sin\left\{(m-n)x\right\} + \sin\left\{(m+n)x\right\}}{2} dx \end{align}上式では，$\sin$関数の加法定理から導出される「積和公式」を使いました．ここで，“$m=n$”の場合は上式の計算結果は次のようになります．
\begin{align} &\cfrac{1}{2} \cdot \int^{2\pi}_{0} 0 + \sin\left\{(m+n)x\right\} dx \nonumber \\ =& \cfrac{1}{2} \cdot \left[ - \cfrac{1}{(m+n)} \cdot \cos \left\{(m+n)x\right\} \right]^{2\pi}_{0} \nonumber \\ =& \ 0 \end{align}また，“$m \neq n$”の場合は次のようになります．
\begin{align} &\cfrac{1}{2} \cdot \int^{2\pi}_{0} \sin\left\{(m-n)x\right\} + \sin\left\{(m+n)x\right\} dx \nonumber \\ =& \cfrac{1}{2} \cdot \left[ - \cfrac{1}{m-n}\cdot \cos\left\{(m-n)x\right\} - \cfrac{1}{(m+n)} \cdot \cos\left\{(m+n)x\right\} \right]^{2\pi}_{0} \nonumber \\ =& \ 0 \end{align}結局，内積“$(\sin(mx),\ \cos(nx))$”の計算結果は次のようにまとめられます．
\begin{equation} (\sin(mx),\ \cos(nx)) = 0 \end{equation}以上のことから，「$\sin$関数と$\cos$関数は周期に関わらずすべて直交している」ことがわかりました．
ここまでの計算により，周期が異なる$\sin$関数と$\cos$関数はすべてが互いに「直交」していることが確認できました．これは，三角関数の集合が「無駄のない基底」を構築していることを表しています．
ここで，「様々な周期の$\sin$関数と$\cos$関数を集めれば，それで基底は全部揃うのか？」という疑問が生じるかと思います．結論としては，「様々な周期の三角関数を集めれば，それで基底として十分である」ことが知られています．厳密な証明は省略しますが，この内容について気になる方は「三角関数の完全性」というキーワードで調べてみてください．
三角関数の直交性を数値計算で確認する実験
プログラムのソース・コード
さきほど計算で確認した「三角関数の直交性」を，マイコンによる数値計算で確認してみましょう．三角関数どうしの内積を計算する関数“inner_product()”のソース・コードをリスト3に示します．このソース・コードを“/* USER CODE BEGIN 0 */”と“/* USER CODE END 0 */”の間に記述します（さきほどの実験で使った“square_wave()”関数の後に記述する）．
この関数の第一引数“mode”は，内積を計算する三角関数の種類を指定するために使います．“$\mathrm{mode}=0$”のときは“$\sin \times \sin$”の内積，“$\mathrm{mode}=1$”のときは“$\cos \times \cos$”の内積，“$\mathrm{mode}=2$”のときは“$\sin \times \cos$”の内積を計算します．
第2引数の“$m$”と第3引数の“$n$”は，内積を計算する三角関数の周期を指定するために使います．これは，さきほどの理論計算で使った“$m$”および“$n$”とまったく同じ役割です．
内積の計算はリスト3の36行目の部分で行われ，計算結果は変数“sum”に格納されます．
|
|---|
| リスト3 三角関数どうしの内積を計算する関数“inner_product()” |
リスト4に示すように，main()関数の“/* USER CODE BEGIN 2 */”から“/* USER CODE END 2 */”の間に関数“inner_product()”を呼び出す処理を記述します．今回は“temp”という変数に内積の計算結果を格納して，printf()関数で表示しています．
|
|---|
| リスト4 sinどうしの内積を計算するmain()関数の記述例 |
実験結果
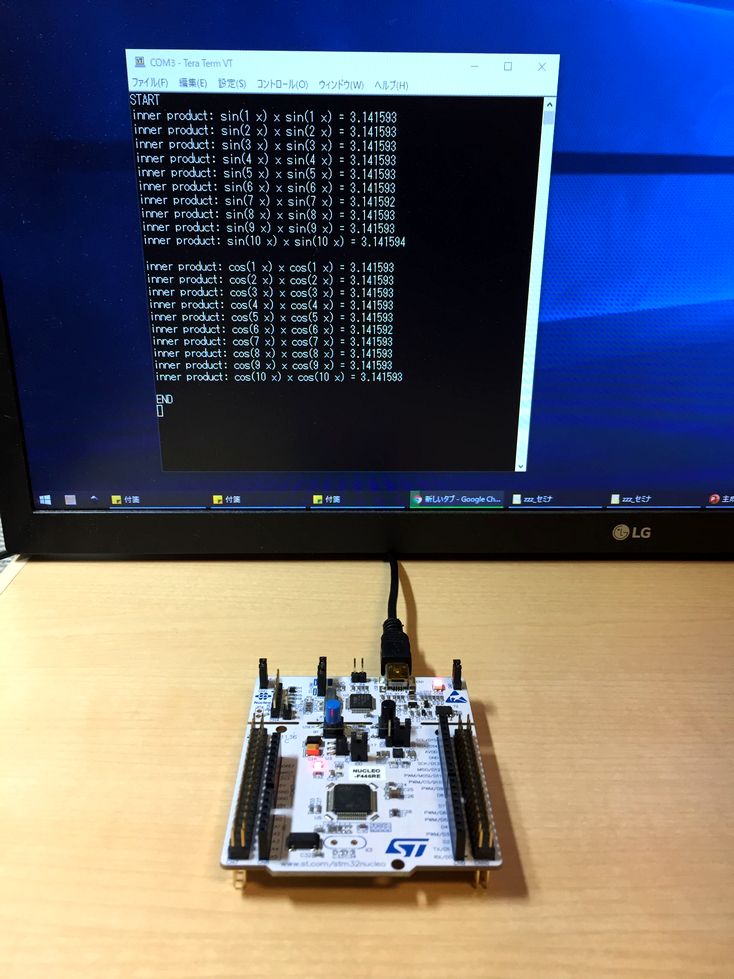
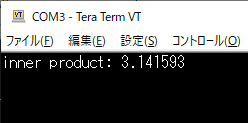
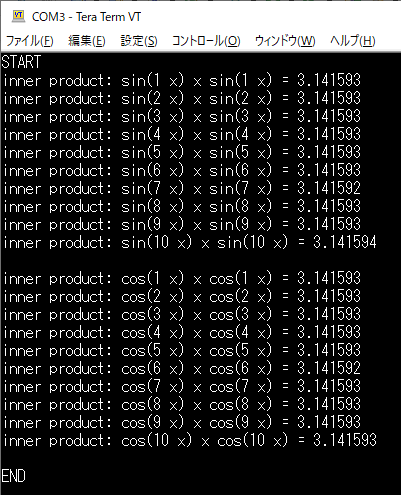
リスト3およびリスト4の内容を追記したプログラムをコンパイルしてマイコンに書き込みます．Tera Termを起動してからマイコンのリセット・スイッチ（黒）を押すと，図16のような結果が表示されます．今回は内積“$(\sin(x),\ \sin(x)$”に相当する計算を行ったので，さきほど理論計算で確認したとおり“$\pi$”の値が計算結果として得られました．
|
|---|
| 図16 リスト4のプログラムの実行結果 |
いろいろな内積のパターンを試してみる
リスト5に，いろいろな周期の$\sin$関数および$\cos$関数どうしの内積を計算するプログラムのソース・コードを示します．周期は“$m=1$”から“$m=10$”までの範囲で計算を行っています．“$n$”についても同様です．
先に理論計算で確認したとおり，周期が異なる$\sin$どうしの内積，周期が異なる$\cos$どうしの内積，さらに$\sin$と$\cos$の内積はすべて“0”になります．そこで，計算結果を見やすくするために内積の値が“0”になる場合は結果を表示しないようにしています．ただし，計算誤差の影響により内積がちょうど“$0.00000\cdots$”になることはないので，計算結果が“0.0001”より小さい場合は「ゼロ」であると判定するようにしています．
|
|---|
| リスト5 三角関数どうしの内積をいろいろなパターンで計算するmain()関数の記述例 |
main()関数の内部の“/* USER CODE BEGIN 2 */”から“/* USER CODE END 2 */”の間をリスト5のように書き換えてコンパイルします．このプログラムを実行すると，図17に示す結果が得られます．理論計算で確認したとおり，同じ周期の$\sin$どうしおよび$\cos$どうしの内積は“$\pi$”になり，それ以外はすべて“0”になるので表示されません．
|
|---|
| 図17 リスト5のプログラムの実行結果 |
「フーリエ級数」の導入
三角関数という「基底」を組み合わせて様々な周期関数を作る
一般の2次元ベクトル“$\bm{A}$”は，$x$方向の基底“$\bm{e}_{x}$”および$y$方向の基底“$\bm{e}_{y}$”を使って次のように表現できるのでした．
\begin{equation} \bm{A} = A_x \cdot \bm{e}_{x} + A_y \cdot \bm{e}_{y} \end{equation}一方で，これまで考えてきたとおり$\sin$や$\cos$といった三角関数は様々な周期関数の「基底」になっています．また，ただの基底ではなく「直交」した基底であることも確認しました．そこで，上式から類推すると様々な周期関数“$f(x)$”は次のように表現できると考えられます．
\begin{align} f(x) &= \cfrac{a_0}{2} \cdot \cos(0) + a_1 \cdot \cos(x) + a_2 \cdot \cos(2x) + \cdots + b_1 \cdot \sin(x) + b_2 \cdot \sin(2x) + \cdots \nonumber \\ &= \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos(kx) + \sum^{\infty}_{k=1} b_k \cdot \sin(kx) \end{align}上式は，「フーリエ級数」（Fourier series）と呼ばれています．また，各項の係数“$a_0$”，“$a_1$”，“$a_2$”，$\cdots$，“$b_1$”,“$b_2$”，$\cdots$は「フーリエ係数」（Fourier coefficients）といいます．“$\cos(0)$”（定数成分）の係数が“$a_{0}/2$”になっているのは，後で帳尻を合わせるためです．また“$\sin(0)=0$”なので，この項はフーリエ係数には含めないのが一般的です．
次回は「フーリエ係数」の求め方を解説
フーリエ級数は，様々な周期関数“$f(x)$”を$\sin$と$\cos$で表すための「ひながた」であると見なせます．そして，各項のフーリエ係数“$a_k$”および“$b_k$”を適当に定めれば，自由自在に周期関数を表現できるだろうと考えられます．次回は，所望の関数を表現するためのフーリエ係数の値を求める方法について考えます．