【Digi-Key社提供】フレッシャーズ＆学生応援特別企画
実験しながら学ぶフーリエ解析とディジタル信号処理
[Vol.4 「フーリエ級数」にもとづいて波形を分析する実験]
スペクトル解析やディジタル・フィルタを最適化してマイコンに実装
- 著者・講師：別府 伸耕/Nobuyasu Beppu (リニア・テック)
- 企画編集・主催： ZEPエンジニアリング株式会社
- 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
- 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
- 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
- 関連製品：［VOD/KIT］STM32マイコン＆Wi-Fiモジュールで学ぶ C/C++プログラミング入門
- 関連記事：Pythonではじめる 数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
- 関連記事：Pythonではじめる 数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]
【Index】
原始的な“DFT”（離散フーリエ変換）を体験する
ディジタル信号処理を“NUCLEO”ボードで実験しながら学ぶ
本連載では，32ビットARM Cortex-M4コアを搭載したワンチップ・マイコンである“STM32F446”で実際に信号処理を実行しながら，ディジタル信号処理の核心を担う理論である「フーリエ解析」を学びます．
実験に必要なのは“STM32F446”の評価ボードである“NUCLEO-F446RE”（2,000円程度）とUSBケーブルだけです(写真1)．ぜひ自分の手でプログラムを書いて実験しながら，信号処理の感覚を身につけてください．
|
|---|
| 写真1 “NUCLEO-F446RE”ボードがあれば本連載で扱う内容をすべて実験できる |
前回導入した「フーリエ級数」の復習
前回のVol.3では，フランスの数学者フーリエ（Joseph Fourier, 1768 - 1830）が提唱した「様々な関数は三角関数の組み合わせで表現できる」という強烈なアイディアを紹介しました．また，この事実を直感的に理解するために，たくさんの$\sin$関数を足し合わせて「矩形波」（くけいは）を作る実験をしました．
一般に，周期が“$2\pi$”の周期関数“$f(x)$”は次式のように様々な周期の$\sin$と$\cos$を組み合わせることで表現できます．このように$\sin$関数や$\cos$関数を無限に足し合わせたものを「フーリエ級数」（Fourier Series）といいます．
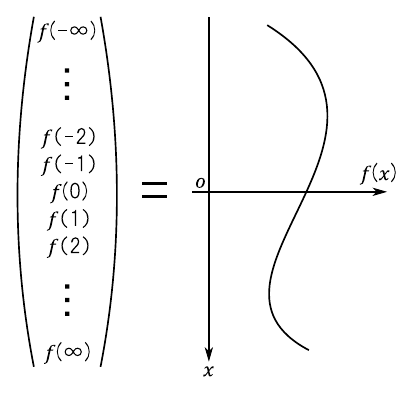
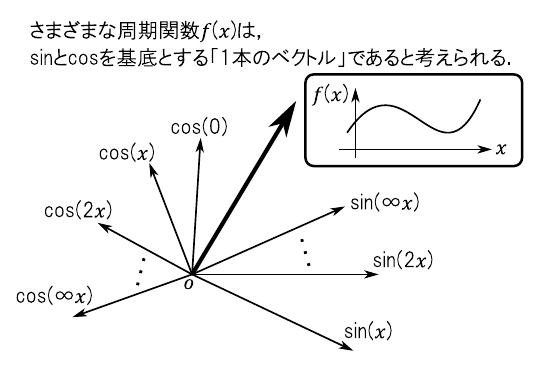
\begin{equation} \label{eq:fourier_series} f(x) = \cfrac{a_0}{2} + \sum^{\infty}_{k=1}a_k \cdot \cos(kx) + \sum^{\infty}_{k=1}b_k \cdot \sin(kx) \end{equation}フーリエ級数の意味を考える上で重要となるのが，図1のように「関数を1つのベクトルと見なす」というアプローチです．図2に示すように関数“$f(x)$”は「無限次元空間にある1本のベクトル」であり，“$\sin$”や“$\cos$”はこの無限次元空間における「基底ベクトル」に相当すると考えられます．このイメージにしたがうと，一般的なベクトルを表現する場合と同様に「各基底を適当な大きさずつ足しあわせる」ことで様々な関数“$f(x)$”を表現できると考えられます．式1のフーリエ級数は，このような考えにもとづいて作られた式でした．
|
|
|---|---|
| 図1 関数は1つの「ベクトル」だと見なせる | 図2 $\sin$や$\cos$は「関数の基底」としてイメージできる |
「フーリエ係数」を求めるプログラムを作る
式1の定数“$a_0,\ a_1,\ a_2, \cdots$”および“$b_1,\ b_2,\ \cdots$”を「フーリエ係数」（Fourier coefficient）といいます．これらの値を定めれば，様々な関数$f(x)$をフーリエ級数の形で表現できます．今回の主題は，対象とする関数“$f(x)$”にあわせて適切な「フーリエ係数」を求める方法を考えることです．
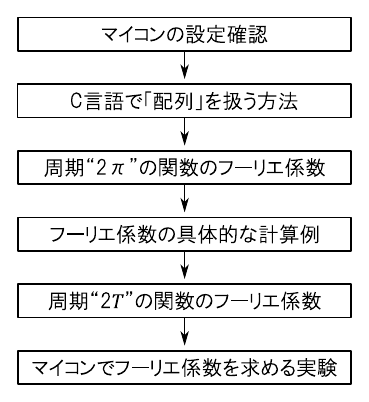
今回の流れを図3に示します．
|
|---|
| 図3 今回の流れ．フーリエ係数をマイコンで計算することを目指す |
今回の実験で作るプログラムは計算量が多いので，マイコンのクロック周波数を最大値に設定しておきます．また，その他のマイコンの設定についても確認します．
C言語のプログラムで「波形データ」を扱う際は，「配列」をよく使います．信号処理のプログラムでは配列を避けて通れないので，「ポインタ」や“malloc()”関数などの基本事項を確認しておくことにします．
続いて，本題である「周期“$2\pi$”の関数のフーリエ係数」を求める方法について考えます．フーリエ係数の計算方法がわかったら，具体的な波形のフーリエ係数を求めてみます．今回は「矩形波」，「全波整流波形」，「三角波」の3種類の波形を扱います．
一般的な周期関数は常に“$2\pi$”の周期であるとは限りません．そこで，ここまで考えた話を一般化して周期が“$2T$”の関数に適用できるフーリエ係数の算出方法を考えます．これで対応可能な範囲が一気に広がります．
最後に，マイコンでフーリエ係数を求めるためのプログラムを作ります．ここで実装する処理は，ディジタル信号処理における「離散フーリエ変換」（DFT）の原型であると言えます．このプログラムを自分で書いて実行すれば，「マイコンを使ってフーリエ解析をする」という感覚がつかめるはずです．
実験の準備
今回の実験は計算量が多いので，マイコンのクロックをできるだけ高速に設定しておきます．例によって，開発環境“STM32CubeIDE”で新しいプロジェクトを作成してプログラムを開発するものとします．
以下，簡単に設定の要点を解説します．開発環境の使い方に関する詳しい説明は本連載のVol.2を参照してください．
ピン・アサインの設定
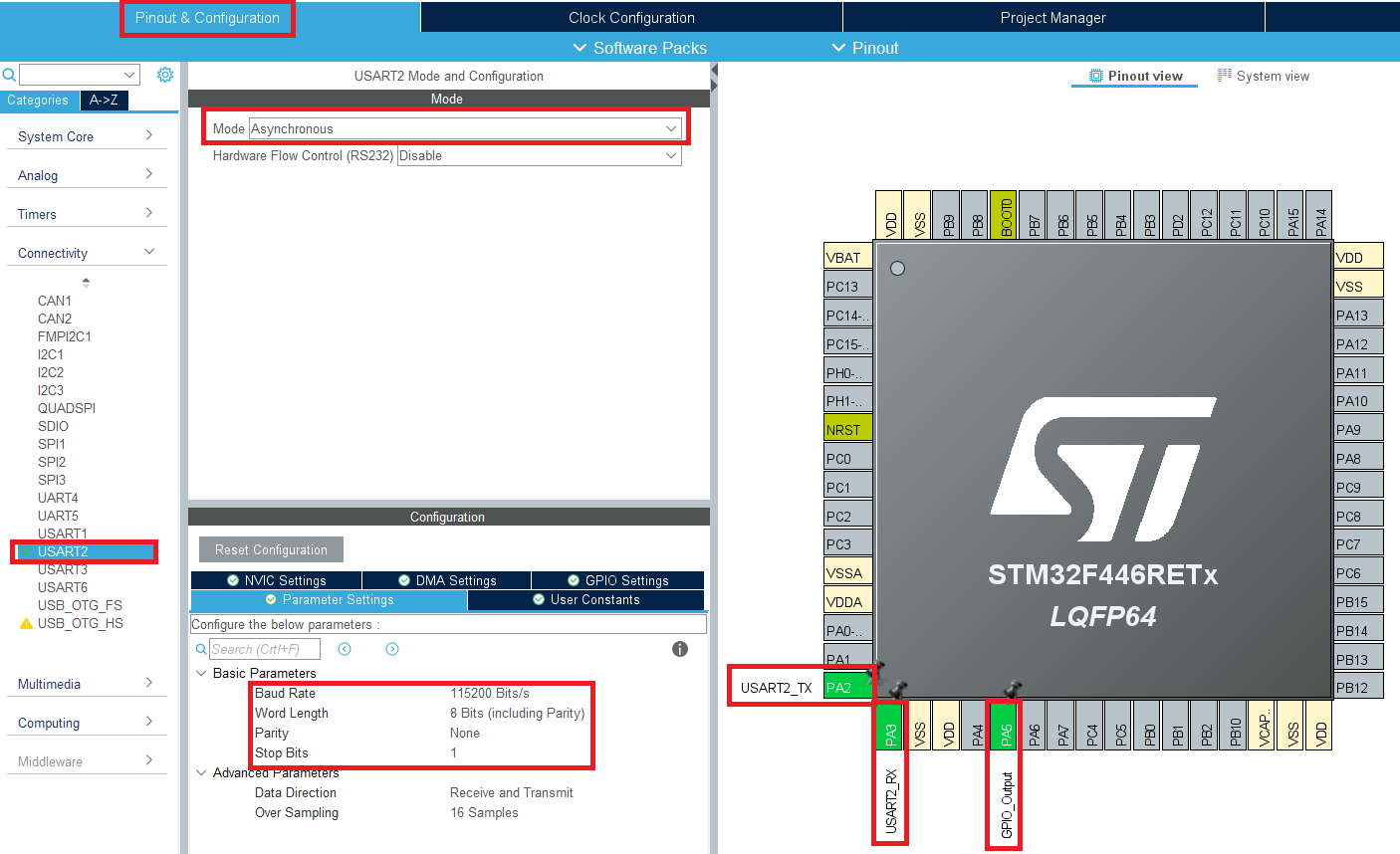
まずは，図4の“Pinout & Configuration”の画面でピンの機能を設定します．
今回も“NUCLEO-F446RE”ボードのUSB経由で計算結果を出力したいので，“PA2”を“USART2_TX”に，“PA3”を“USART2_RX”に設定します．また，画面左側の“Categories”一覧で[Connectivity] - [USART2] を選択し，“Mode”の欄で“Asynchronous”を選択します．これでUSARTモジュール（今回は非同期の“UART”として使う）がアクティブになります．
ボー・レート（Baud Rate）などの設定はデフォルトのままで結構です．念のため“Baud Rate: 115200 Bits/s”，“Word Length: 8 Bits”，“Parity; None”，“Stop Bits: 1”となっていることを確認してください．
なお，図4では“PA5”を“GPIO_Output”に設定しています．これは，NUCLEOボード上の緑色LEDを光らせるためです．今回は積極的に緑色LEDを使いませんが，デバッグに便利なのでこのように設定しておきます．
|
|---|
| 図4 “Pinout & Configuration”画面で各ピンの機能を設定する |
クロックの設定
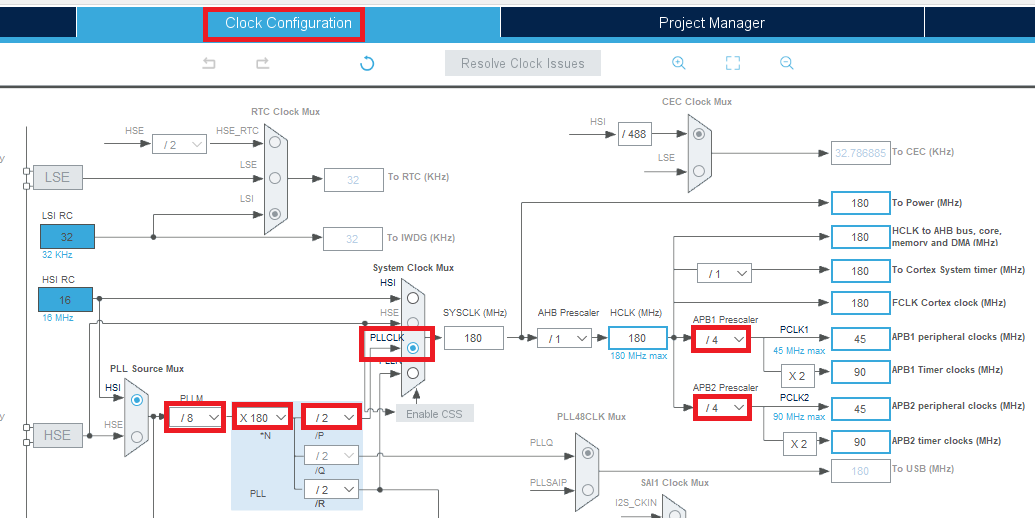
続いて，図5の“Clock Configuration”画面を開いてクロックの設定をします．今回は“STM32F446”マイコンの最大クロック周波数である“180 MHz”で動かすことにします．
図5の中央付近にあるマルチプレクサ“System Clock Mux”で，PLLの出力である“PLLCLK”を選択します．“PLL”（Phase Locked Loop）は，おおもとのクロック源である“HSI RC”の16 MHzを基準として様々な周波数のクロック信号を作り出す回路です．今回は“PLLM”の欄を“/ 8”（8分周），“*N”の欄を“X 180”（180逓倍），“/P”の欄を“/ 2”（2分周）に設定して“$16 \div 8 \times 180 \div 2 = 180 \ \mathrm{MHz}$”のクロック信号を作ります．
なお，UARTやADCといった周辺モジュールの動作速度はCPUコアよりも遅いので，適宜クロックを分周しておきます．今回は“APB1 Prescaler”の欄を“/ 4”（4分周），“APB2 Prescaler”の欄を“/ 4”（4分周）にします．
もし「クロック周波数が大きすぎる」などの問題が生じた場合は，問題箇所の項目が赤くなります．図5と見比べながら値を修正してください．
|
|---|
| 図5 “Clock Configuration”画面でシステム・クロックを最大の180 MHzに設定する |
“printf()”関数を使うための設定
パソコンに対してUART経由で文字列を出力するとき，“printf()”関数が使えると便利です．そのための準備をしておきましょう．
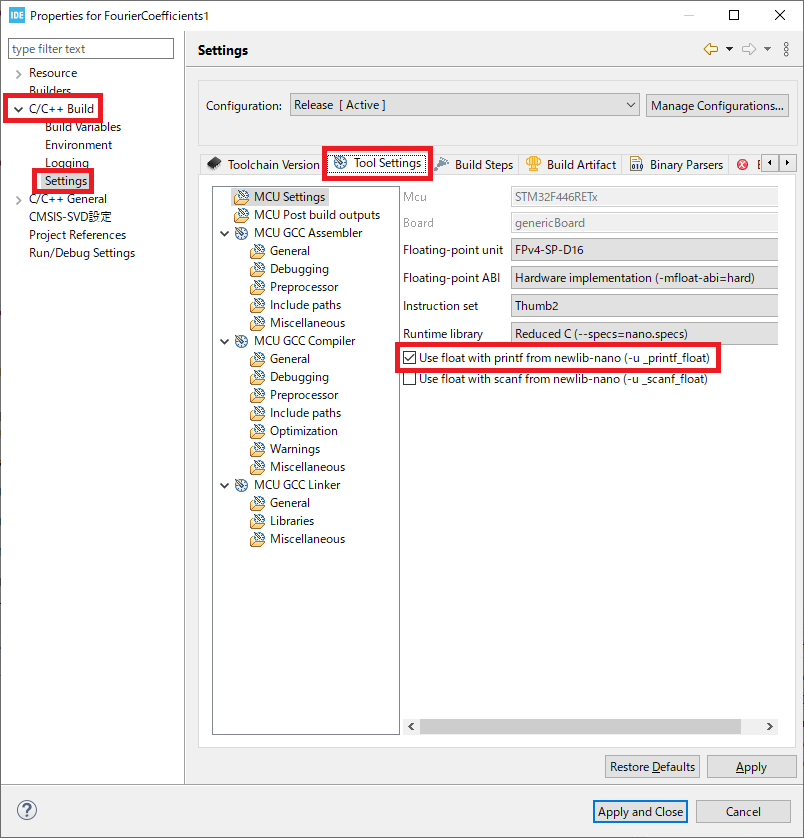
まずはメニュー・バーから [Project] - [Properties] をクリックして図6の画面を開きます．“C/C++ Build”の項目を展開して“Settings”をクリックし，“Tool Settings”タブを開きます．ここで“Use float with printf from newlib-nano”にチェックを付けて[Apply and Close]ボタンをクリックします．これでprintf()関数でfloat型の数値を出力できるようになります．
|
|---|
| 図6 “printf()”関数でfloat型の数値を表示できるようにする |
続いて，ソース・ファイル“main.c”の冒頭の“USER CODE BEGIN Includes”の部分にリスト1の内容を記述します．“stdio.h”はprintf()関数を使うため，“math.h”はsinやcosなどの計算を行うため，“stdlib.h”は後で解説する“malloc()”関数を使うためにインクルードしています．
|
|---|
| リスト1 必要なヘッダ・ファイルをインクルードする |
さらに，printf()関数の標準出力をUARTに設定するために，リスト2に示す“_write()”関数を定義しておきます．この内容は“/* USER CODE BEGIN 0 */”から“/* USER CODE END 0 */”の間に記述します．
|
|---|
| リスト2 標準出力をUARTに設定するために“_write()”関数を定義する |
C言語で配列を扱う方法の確認
信号処理のプログラムでは「配列」を多用する
マイコンを使った信号処理では，測定結果や波形のデータを扱うために「配列」（array）をよく使います．C言語で配列を扱うテクニックは信号処理のプログラムを書く上でとても役立つので，重要な項目を簡単に確認しておきます．
配列データのメモリ上の配置
ここでは例として，リスト3のようにint型のデータを4個格納できる“a”という配列を定義したとします．
|
|---|
| リスト3 int型のデータを4個格納できる配列“a”を定義する |
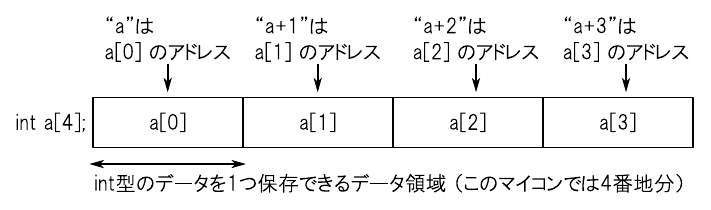
このとき，マイコンのメモリ上にはint型のデータを連続して4個保存する領域が図7のように用意されます．
|
|---|
| 図7 “int a[4];”を定義したときに確保されるメモリ領域 |
ソース・コード上でこの配列の名前“a”を記述すると，これは「配列“a”の先頭のアドレス値」として扱われます．これは，1番目のデータ“a[0]”のアドレスと同義です．また，“a+1”と書いた場合は2番目のデータである“a[1]”のアドレス値を意味します．
実際にmain()関数の“/* USER CODE BEGIN 2 */”から“/* USER CODE END 2 */”の間にリスト4の内容を記述して，簡単な実験をしてみましょう．
|
|---|
| リスト4 配列“a”を定義してから“a”および“a+1”の値そのものを出力する |
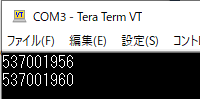
パソコン側で“Tera Pad”などのターミナル・ソフトを起動してからマイコン側でリスト4のプログラムを実行すると，図8のような出力結果が得られます．
|
|---|
| 図8 「リスト4」のプログラムを実行した様子 |
新しく定義した配列“int a[4]”のデータをメモリ上のどこに置くかは，コンパイラが自動的に決めます．図8より，今回は“537001956”番地を先頭とするメモリ領域が確保されたようです．また，2番目のデータである“a[1]”が保存されるアドレスは“537001960”となっています．
配列のデータはメモリ上で連続して並ぶように配置されるので，「int型のデータ」を1個保存するためには$537001960 - 537001956 = 4$ アドレス分のメモリ領域を消費することがわかります（1アドレスあたり保存できるデータが8ビットなら，int型は32ビット長ということになる）．
以上の実験で確認できたとおり，配列の名前“a”は「メモリ上のアドレスの値」として扱われます．ソース・コード上で“a+1”と記述した場合，その値は数値的な“a+1”とは必ずしも一致しません．なお，配列“a”をchar型やlong型，float型やdouble型で定義すると“a”と“a+1”の間隔が変化します．実験してみてください．
間接参照演算子“*”の使い方
今度は，配列“a”をリスト5のように初期値を指定して定義したとします．
|
|---|
| リスト5 配列“a”を定義し，初期値も定める |
このように配列を定義した状態で“a[0]”と記述すれば，“1”という数値データを取り出すことができます．同様に，“a[1]”と記述すれば“2”という数値データにアクセスできます．
ここで，「間接参照演算子」（indirection operator）“*”を使うことを考えます．この演算子“*”を何らかの「アドレス値を保存している変数」の前につけると，そのアドレスに保存されているデータを取り出すことができます．すなわち，“*a”と書けば配列“a”の1番目のデータである“a[0]”にアクセスでき，“*(a+1)”と書けば2番目のデータ“a[1]”にアクセスできます．これを実験で確かめてみましょう．
|
|---|
| リスト6 間接参照演算子“*”を使う実験 |
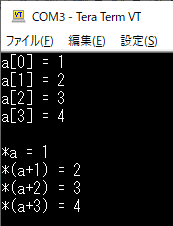
main()関数内部の/* USER CODE BEGIN 2 */から/* USER CODE END 2 */の間にリスト5の内容を記述します．ソース・コードの前半では“a[0]”，“a[1]”といった形で配列の要素にアクセスしています．一方で，ソース・コードの後半では“*a”や“*(a+1)”という具合にアドレスを意識した形でデータを参照しています．
リスト6のプログラムを実行すると，図9のような出力結果が得られます．この結果から，ソース・コード上では“a$[ x ]$”と“*($\mathrm{a} + x$)”は同じ意味になることがわかります．“int a[4]”という配列を定義した時点で，コンパイラは「int型だから各データのアドレス間隔は“4”だ」ということを認識しています．そのため，先ほど確認したとおり“a”，“a+1”，“a+2”といった値の差分は“4”になります．これにより，“*a”，“*(a+1)”，“*(a+2)”という記述によって各データの内容を正しく参照できるようになっています．
|
|---|
| 図9 「リスト6」のプログラムを実行した様子 |
配列の長さを別の変数で指定したいときは“malloc()”関数を使う
いろいろなプログラムを書いていると，配列を定義するときに長さを固定せず，別の変数で長さを指定したい時があります．このような場合に便利なのが“malloc()”関数です．“malloc”（マロック）は“memory allocation”の略で，直訳すると「メモリを割り当てる」という意味です．
例えば，int型のデータを4個もつ配列“a”をmalloc()関数を使って用意したい時はリスト7のように記述します．
|
|---|
| リスト7 “malloc()”関数でint型のデータを4個格納できる配列“a”を定義する |
malloc()関数の引数は，確保するメモリ領域の大きさを指定します．今回はint型のデータを4個保存できる領域を確保したいので，“sizeof(int) * 4”としています．なお，“sizeof()”関数は各データ型に必要なメモリ領域の大きさ（アドレス長）を返す関数です．このマイコンの場合，“sizeof(int)”は“4”，“sizeof(char)”は“1”といった値になります．
malloc()関数で確保されるメモリ領域の場所は，コンパイラによって自動的に決められます．その結果として，malloc()関数は確保したメモリ領域の先頭のアドレスを返します．今回はそれを“a”という変数で受けています．なお，“a”は「int型のアドレスを保持する変数」なので“int*”という型で定義しています．いわゆる「ポインタ」（pointer）です．
malloc()関数で確保したメモリ領域を使い終わったら，“free()”関数で解放しておくことをおすすめします．メモリ領域は有限なので，無暗にmalloc()を使い続けるとメモリ不足に陥る可能性があります（いわゆる「メモリ・リーク」）．先ほど確保したメモリ領域（配列）“a”を解放する場合は，リスト8のように記述します．
|
|---|
| リスト8 使い終わったメモリ領域はfree()で解放しておく |
それでは，malloc()関数を使う実験をしてみましょう．配列“a”の長さを“data_num”（the number of dataの略）という変数で指定して，値を読み書きする例をリスト9に示します．
|
|---|
| リスト9 malloc()関数を使って配列を動的に確保する実験 |
リスト9のプログラムの実行結果を図10に示します．今回は“data_num = 10”として，配列の長さを“10”にしました．これに伴い，プログラム中のfor文の繰り返し回数もすべて“10”となります．変数“data_num”をいろいろな値に変えて実験してみてください．
|
|---|
| 図10 「リスト9」のプログラムを実行した様子 |
関数に配列を渡す
C言語では，関数に対して配列のデータをまるごと渡すことができません．そこで，「配列の先頭のアドレスを渡す」 という方法がよく使われます．
先に確認したとおり，配列を定義するとコンパイラはメモリ領域を連番で取得します．そのため，配列“a”の先頭のアドレスさえわかれば“a+1”は2番目のデータのアドレス，“a+2”は3番目のデータのアドレスといった具合に順番にデータをたどることができます．ただし，配列を受け取る関数は「配列の長さ」を知らないので，これも関数の引数として渡すようにするのが一般的です．
関数に配列データを渡す実験をしてみましょう．リスト10で定義されている関数“print_array()”は，引数“array”の内容をprintf()関数で表示します．引数“data_num”で配列の長さを指定しています．これを“/* USER CODE BEGIN 0 */”から“/* USER CODE END 0 */”の間（先に用意した“_write()”関数の後ろなど）に記述します．
|
|---|
| リスト10 配列を受け取る関数の例 |
関数“print_array()”を定義したら，リスト11のようにmain()関数の中で使ってみます．
|
|---|
| リスト11 関数に配列を渡す実験 |
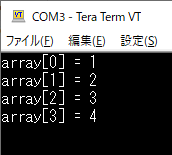
リスト11のプログラムを実行した様子を図11に示します．配列“a”の先頭のアドレスを利用して，関数が配列のデータにアクセスできていることがわかります．今回は配列のデータを読み込むだけでしたが，関数内で配列に値を書き込むこともできます．
|
|---|
| 図11 「リスト11」のプログラムを実行した様子 |
周期“$2\pi$”の関数のフーリエ係数
フーリエ係数“$a_k$”を求める方法
本題の「フーリエ係数」の話題に入ります．次式の「フーリエ級数」は，周期“$2\pi$”の関数“$f(x)$”を表す「ひな型」であると言えます．
\begin{equation} f(x) = \cfrac{a_0}{2} + \sum^{\infty}_{k=1}a_k \cdot \cos(kx) + \sum^{\infty}_{k=1}b_k \cdot \sin(kx) \end{equation}特定の関数“$f(x)$”をうまく表せるように係数“$a_0,\ a_1,\ \cdots , $”および係数“$b_1,\ b_2,\ \cdots$”を定めれば，その関数をフーリエ級数で表現できたことになります．まずは，フーリエ係数“$a_k$”（$k \geqq 1$）を求める方法について考えます．
係数“$a_k$”は，「関数“$f(x)$”がどれくらい“$\cos(kx)$”の成分を含んでいるか」を表しています．よって，係数“$a_k$”の大きさを求めるには「関数“$f(x)$”と“$\cos(kx)$”との内積」を計算すれば良いと考えられます（「関数の内積」については前回のVol.3を参照）．関数“$f(x)$”の周期は“$2\pi$”なので，内積計算の積分範囲は“$0 \leqq x \leqq 2\pi$”とします．
\begin{equation} \label{eq:coeff_ak_0} ( f(x),\ \cos(kx) )= \int^{2\pi}_{0} f(x) \cdot \cos(kx)\ dx \end{equation}くどいですが，係数“$a_k$”は関数“$f(x)$”に含まれる“$\cos(kx)$”の振動成分の大きさを表します．そのため，もし“$f(x) = \cos(kx)$”すなわち「関数“$f(x)$”が“$\cos(kx)$”そのもの」ならば，“$a_k$”=1となる必要があります．そこで，試しに“$f(x)=\cos(kx)$”を上式に代入してみます．
\begin{align} \int^{2\pi}_{0} \cos(kx) \cdot \cos(kx)\ dx &= \int^{2\pi}_{0} \cfrac{1 + \cos(2kx)}{2} \ dx \nonumber \\ &= \cfrac{1}{2}\cdot \left[ x + \cfrac{1}{2k}\cdot \sin(2kx) \right]^{2\pi}_{0} \nonumber \\ &= \pi \end{align}上式より，“$\cos(kx)$”どうしの内積を計算すると“$\pi$”という値になります．よって，係数“$a_k$”を求めるためには式3の両辺を“$\pi$”で割り算すれば良いと考えられます．これは，いわゆる「規格化」あるいは「正規化」（normalization）の処理に相当します．
\begin{equation} \label{eq:coeff_ak_1} a_k = \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \cos(kx)\ dx \end{equation}なお，ここでは関数“$f(x)$”の周期を“$2\pi$”であると仮定しており，“$\cos(kx)$”も長さ“$2\pi$”の範囲にちょうど収まります（周期が“$2\pi / k$”だから）．そのため，「関数どうしの内積」を求める際の積分範囲は「積分区間の長さが“$2\pi$”」になっていればどのようにとっても構いません．教科書によっては次式のように積分範囲を“$-\pi \leqq x \leqq \pi$”としている場合もありますが，いずれにしても計算結果は同じです．
\begin{equation} \label{eq:coeff_ak_2} a_k = \cfrac{1}{\pi} \int^{\pi}_{-\pi} f(x) \cdot \cos(kx)\ dx \end{equation}前回のVol.3で確認したとおり，周期が異なる“$\cos$”関数どうしには「直交性」があるのでした．すなわち，次式が成り立ちます．
\begin{equation} (\cos(mx),\ \cos(nx)) = \left\{ \begin{array}{ll} \pi & (m = n) \\ 0 & (m \neq n)\\ \end{array} \right. \end{equation}上式より，式5や式6の計算では“$k$”で指定した周期の“$\cos$”関数の成分だけが抽出され，それ以外の振動成分は無視されます．
フーリエ係数“$b_k$”を求める方法
続いて，フーリエ係数“$b_k$”を求める方法を考えます．基本的な流れは係数“$a_k$”のときと同じです．
係数“$b_k$”は，「対象とする関数“$f(x)$”が“$\sin(kx)$”の振動成分をどれほど含んでいるか」を表す値です．よって，係数“$b_k$”を求めるには「関数“$f(x)$”と“$\sin(kx)$”との内積」を計算すれば良いと考えられます．
\begin{equation} \label{eq:coeff_bk_1} (f(x), \sin(kx)) = \int^{2\pi}_{0} f(x) \cdot \sin(kx) \, dx \end{equation}ここで，関数“$f(x)$”が“$\sin(kx)$”そのものだった場合，上式の内積の値は“$\pi$”になります．
\begin{align} \int^{2\pi}_{0} \sin(kx) \cdot \sin(kx) \, dx &= \int^{2\pi}_{0} \cfrac{1 - \cos(2kx)}{2} \, dx \nonumber \\ &= \cfrac{1}{2} \cdot \left[ x - \cfrac{1}{2k} \cdot \sin(2kx) \right]^{2\pi}_{0} \nonumber \\ &= \pi \end{align}よって，式8の両辺を“$\pi$”で割って「正規化」すれば係数“$b_k$”が得られます．
\begin{equation} \label{eq:coeff_bk_2} b_k = \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \sin(kx) \, dx \end{equation}係数“$a_k$”の場合と同様に，積分範囲を“$-\pi \leqq x \leqq \pi$”としても同じ結果が得られます．
\begin{equation} \label{eq:coeff_bk_3} b_k = \cfrac{1}{\pi} \int^{\pi}_{-\pi} f(x) \cdot \sin(kx) \, dx \end{equation}前回のVol.3で確認したとおり，周期が同じ$\sin$関数どうしの内積は“$\pi$”になり，周期が異なる$\sin$関数どうしの内積は“0”になるのでした．
\begin{equation} (\sin(mx),\ \sin(nx)) = \left\{ \begin{array}{ll} \pi & (m = n) \\ 0 & (m \neq n)\\ \end{array} \right. \end{equation}上式より，式10や式11の計算では“$k$”で指定した周期をもつ“$\sin$”関数の成分だけが抽出され，それ以外の振動成分は無視されます．
フーリエ係数“$a_0$”を求める方法
フーリエ係数“$a_0$”が含まれる項はいわゆる「定数項」で，波形でいうところの「オフセット」に相当します．係数“$a_0$”の大きさは，「関数“$f(x)$”がどれくらい“$\cos(0 \cdot x)$ = 1”の成分を含んでいるか」を表しています（“$\sin(0 \cdot x) = 0$”なので“$b_0$”は無い）．よって，係数“$a_0$”を求めるには「関数“$f(x)$”と“1”の内積」を求めれば良いと考えられます．
\begin{equation} \label{eq:coeff_a0_1} (f(x), 1) = \int^{2\pi}_{0} f(x) \cdot 1 \ dx \end{equation}ここで，関数“$f(x)$”が“$f(x) = 1$”である場合を考えます．このとき，上式の内積は次のように計算できます．
\begin{align} \int^{2\pi}_{0} 1 \cdot 1 \ dx &= [x]^{2\pi}_{0} \nonumber \\ &= 2\pi \end{align}上式より，係数“$a_0$”を求めるには式13の両辺を“$2\pi$”で割って正規化する必要があります．しかし，ここまで求めたフーリエ係数“$a_k$”（$k \geqq 1$）や係数“$b_k$”は正規化するために“$\pi$”で割り算していたので，係数“$a_0$”だけ“$2\pi$”で割り算するというのは統一感がありません．そこで，すべてのフーリエ級数は“$\pi$”で割り算する形で表現しておき，後で「フーリエ級数」のほうで帳尻を合わせることにします．
\begin{equation} \label{eq:coeff_a0_2} a_0 = \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \, dx \end{equation}なお，積分範囲を“$-\pi \leqq x \leqq \pi$”としても同じ結果が得られます．
\begin{equation} \label{eq:coeff_a0_3} a_0 = \cfrac{1}{\pi} \int^{\pi}_{-\pi} f(x) \, dx \end{equation}周期“$2\pi$”の関数のフーリエ係数まとめ
以上のことから，フーリエ係数“$a_0$”，“$a_k$”，“$b_k$”を求める式がそろいました．
\begin{align} a_0 &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \, dx \\ a_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \cos(kx) \, dx\\ b_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \sin(kx) \, dx \end{align}上式で得られたフーリエ係数を使って“$\cos$”や“$\sin$”といった振動成分およびオフセット（定数項）を組み合わせると，関数“$f(x)$”を次式のように表現できます．これが，いわゆる「フーリエ級数」です．
\begin{equation} f(x) = \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos(kx) + \sum^{\infty}_{k=1} b_k \cdot \sin(kx) \end{equation}なお，“$a_0$”だけ“1/2”倍されているのは先ほど説明した帳尻合わせのためです．
周期“$2\pi$”のフーリエ級数の例
具体的にフーリエ係数を求める方法がわかったので，代表的な関数をフーリエ級数で表現してみることにします．
矩形波のフーリエ級数展開
|
|---|
| 図12 今回扱う矩形波 |
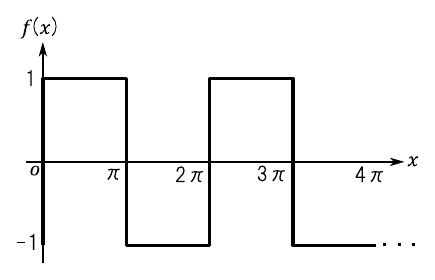
「矩形波」（くけいは，square wave）とは，図12のような波形を指します．ディジタル回路で扱う「パルス信号」などが矩形波に相当します．この波形をフーリエ級数で表現してみましょう．
今回扱う矩形波を表す関数“$f(x)$”を次のように定義します．なお，式22は関数“$f(x)$”が周期“$2\pi$”で限りなく続く波形であることを表しています．
\begin{equation} f(x) = \left\{ \begin{array}{cc} 1 & (0 \leqq x < \pi) \\ -1 & (\pi \leqq x < 2\pi) \end{array} \right. \end{equation} \begin{equation} \label{eq:period_2pi} f(x + 2\pi) = f(x) \end{equation}まずはフーリエ係数“$a_0$”を求めます．
\begin{align} \label{eq:square_a0} a_0 &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} 1 \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -1 \, dx \nonumber \\ &= 1 - 1 \nonumber \\ &= 0 \end{align}上式より，“$a_0 = 0$”であることがわかりました．これは図12の波形に「オフセット」が無いことからも納得できるかと思います．
続いて，フーリエ係数“$a_k$”を求めます．
\begin{align} \label{eq:square_ak} a_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \cos(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} 1 \cdot \cos(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -1 \cdot \cos(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \cdot \left[ \cfrac{1}{k} \cdot \sin(kx) \right]^{\pi}_{0} + \cfrac{1}{\pi} \cdot \left[ - \cfrac{1}{k} \cdot \sin(kx) \right]^{2\pi}_{\pi} \nonumber \\ &= \cfrac{1}{\pi} \cdot (0 - 0) + \cfrac{1}{\pi} \cdot (0 - 0) \nonumber \\ &= 0 \end{align}上式より，“$a_k = 0$”であることがわかりました．$\cos$関数は“$f(-x) = f(x) $”を満たすのでいわゆる「偶関数」ですが，図12の矩形波は“$f(-x) = -f(x)$”となる「奇関数」です．よって偶関数である“$\cos(kx)$”の成分は一切含まれていないということで，“$a_k = 0$”となったものと考えられます．
最後に，フーリエ係数“$b_k$”を求めます．
\begin{align} b_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \sin(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} 1 \cdot \sin(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -1 \cdot \sin(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \cdot \left[ - \cfrac{1}{k} \cdot \cos(kx) \right]^{\pi}_{0} + \cfrac{1}{\pi} \cdot \left[ \cfrac{1}{k} \cdot \cos(kx) \right]^{2\pi}_{\pi} \nonumber \\ &= \cfrac{1}{\pi k} \cdot \left\{ 2 - 2 \cdot \cos(k \cdot \pi) \right\} \end{align}ここで“$n$”を整数とすると，“$\cos(2n \cdot \pi) = 1$”および“$\cos\left\{ (2n-1)\cdot \pi \right\} = -1$”が成り立ちます．よって，次のように場合分けできます．
\begin{equation} \label{eq:square_bk} b_k = \left\{ \begin{array}{cc} 0 & (k = 2n) \\ \cfrac{4}{\pi k} & (k = 2n-1) \end{array} \right. \end{equation}以上のことから，「矩形波」のフーリエ級数は次のように表せます．
\begin{align} \label{eq:square_series} f(x) &= \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos(kx) + \sum^{\infty}_{k=1} b_k \cdot \sin(kx) \nonumber \\ &= \cfrac{4}{\pi} \cdot \sum^{\infty}_{k=1} \cfrac{1}{(2k-1)} \cdot \sin\left\{ (2k-1)\cdot x \right\} \nonumber \\ &= \cfrac{4}{\pi} \cdot \left\{ \sin(x) + \cfrac{1}{3}\cdot \sin(3x) + \cfrac{1}{5}\cdot \sin(5x) + \cdots \right\} \end{align}前回のVol.3で「$\sin$関数を組み合わせて矩形波を作る実験」をしましたが，あの時に使った式は上記の手順で求めたものです．
全波整流波形のフーリエ級数展開
|
|---|
| 図13 今回扱う全波整流波形 |
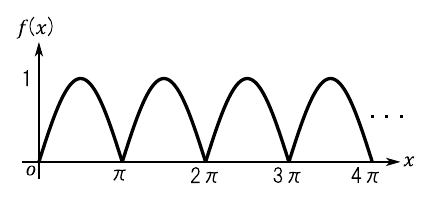
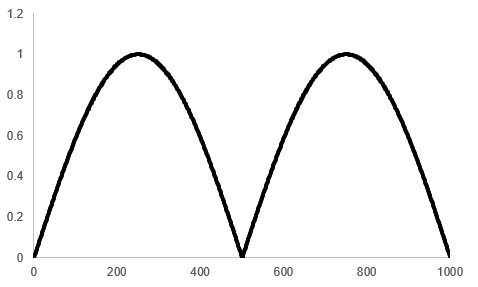
「全波整流波形」（full wave rectified waveform）とは，図13のような波形を指します．電源回路などに使われるブリッジ・ダイオードに対して交流波形を印加すると，全波整流波形が得られます．この波形をフーリエ級数で表してみましょう．
今回扱う全波整流波形を次のような関数“$f(x)$”で定義します．
\begin{equation} f(x) = \left\{ \begin{array}{cc} \sin(x) & (0 \leqq x < \pi) \\ -\sin(x) & (\pi \leqq x < 2\pi) \end{array} \right. \end{equation} \begin{equation} f(x + 2\pi) = f(x) \end{equation}フーリエ係数“$a_0$”を求めます．
\begin{align} \label{eq:full_wave_a0} a_0 &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} \sin(x) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -\sin(x) \, dx \nonumber \\ &= \cfrac{1}{\pi}\cdot \left[ -\cos(x) \right]^{\pi}_{0} + \cfrac{1}{\pi} \cdot \left[ \cos(x) \right]^{2\pi}_{\pi} \nonumber \\ &= \cfrac{4}{\pi} \end{align}続いて，フーリエ係数“$a_k$”を求めます．
\begin{align} a_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \cos(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} \sin(x) \cdot \cos(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -\sin(x) \cdot \cos(kx) \, dx \end{align}ここで，Vol.1の記事で導出した「$\sin$の加法定理」を思い出します．
\begin{align} \left\{ \begin{array}{c} \sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b) \\ \sin(a-b) = \sin(a)\cos(b) - \cos(a)\sin(b) \end{array} \right. \end{align}上式において“$a = x$”，“$b = kx$”として第1式と第2式を加算すると，次式が得られます．
\begin{align} \sin(x) \cdot \cos(kx) &= \cfrac{\sin\left\{(k+1)x \right\} + \sin\left\{ (1-k)x \right\} }{2} \nonumber \\ &= \cfrac{ \sin \left\{ (k+1) x \right\} - \sin \left\{ (k-1) x \right\} }{2} \end{align}よって，“$a_k$”は次のように計算できます．
\begin{align} a_k &= \cfrac{1}{\pi} \int^{\pi}_{0} \sin(x) \cdot \cos(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -\sin(x) \cdot \cos(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} \cfrac{ \sin\left\{(k+1) x\right\} - \sin\left\{(k-1)x \right\}}{2} \, dx - \cfrac{1}{\pi} \int^{2\pi}_{\pi} \cfrac{ \sin\left\{(k+1) x\right\} - \sin\left\{(k-1)x \right\}}{2} \, dx \nonumber \\ &= \cfrac{1}{2\pi} \left[ -\cfrac{\cos\left\{(k+1)x \right\}}{k+1} + \cfrac{\cos\left\{(k-1)x \right\}}{k-1} \right]^{\pi}_{0} - \cfrac{1}{2\pi} \left[ -\cfrac{\cos\left\{(k+1)x \right\}}{k+1} + \cfrac{\cos\left\{(k-1)x \right\}}{k-1} \right]^{2\pi}_{\pi} \nonumber \\ &= \cfrac{1}{2\pi} \left[ -\cfrac{\cos\left\{(k+1)\pi \right\}}{k+1} + \cfrac{\cos\left\{(k-1)\pi \right\}}{k-1} + \cfrac{1}{k+1} - \cfrac{1}{k-1} \right] \nonumber \\ &- \cfrac{1}{2\pi} \left[ -\cfrac{1}{k+1} + \cfrac{1}{k-1} + \cfrac{\cos\left\{ (k+1)\pi \right\}}{k+1} - \cfrac{\cos\left\{(k-1)\pi \right\}}{k-1} \right] \nonumber \\ &= \cfrac{1}{\pi} \left[ \cfrac{1}{k+1} - \cfrac{1}{k-1} + \cfrac{\cos\left\{(k-1)x \right\}}{k-1} - \cfrac{\cos\left\{(k+1) x\right\}}{k+1} \right] \end{align}ここで“$n$”を整数とすると，“$\cos(2n \cdot \pi) = 1$”および“$\cos\left\{ (2n-1)\cdot \pi \right\} = -1$”が成り立ちます．よって，次のように場合分けできます．
\begin{equation} \label{eq:full_wave_ak} a_k = \left\{ \begin{array}{cc} \cfrac{2}{\pi} \left( \cfrac{1}{k+1} - \cfrac{1}{k-1} \right) = -\cfrac{4}{\pi}\cdot \cfrac{1}{(k+1)(k-1)} & (k = 2n) \\ 0 & (k = 2n -1) \end{array} \right. \end{equation}最後に，フーリエ係数“$b_k$”を求めます．全波整流波形は“$f(-x) = f(x)$”を満たす「偶関数」なので“$b_k = 0$”であると考えられますが（$\sin$は奇関数だから），念のため計算しておきます．
\begin{align} b_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \sin(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} \sin(x) \cdot \sin(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -\sin(x) \cdot \sin(kx) \, dx \end{align}ここで，Vol.1の記事で導出した「$\cos$の加法定理」を思い出します．
\begin{eqnarray} \left\{ \begin{array}{c} \cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b) \\ \cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b) \end{array} \right. \end{eqnarray}上式において“$a=x$”，“$b=kx$”として第2式から第1式を引き算すると次式が得られます．
\begin{align} \sin(x) \cdot \sin(kx) &= \cfrac{ \cos \left\{ (1-k)x \right\} - \cos \left\{ (1+k)x \right\} }{2} \nonumber \\ &= \cfrac{ \cos \left\{ (k-1)x \right\} - \cos \left\{ (k+1)x \right\} }{2} \end{align}よって，“$b_k$”は次のように計算できます．
\begin{align} \label{eq:full_wave_bk} b_k &= \cfrac{1}{\pi} \int^{\pi}_{0} \sin(x) \cdot \sin(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -\sin(x) \cdot \sin(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} \cfrac{\cos \left\{(k-1)x \right\} - \cos \left\{(k+1)x \right\}}{2} \, dx - \cfrac{1}{\pi} \int^{2\pi}_{\pi} \cfrac{ \cos \left\{ (k-1)x \right\} - \cos \left\{ (k+1)x \right\} }{2} \, dx \nonumber \\ &= \cfrac{1}{2\pi} \left[ \cfrac{\sin\left\{(k-1)x \right\} }{k-1} - \cfrac{\sin\left\{ (k+1) x\right\}}{k+1} \right]^{\pi}_{0} - \cfrac{1}{2\pi}\left[ \cfrac{\sin\left\{(k-1)x \right\} }{k-1} - \cfrac{\sin\left\{ (k+1) x\right\}}{k+1} \right]^{2\pi}_{\pi} \nonumber \\ &= 0 \end{align}以上のことから，「全波整流波形」のフーリエ級数は次のように表せます．
\begin{align} \label{eq:full_wave_series} f(x) &= \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos(kx) + \sum^{\infty}_{k=1} b_k \cdot \sin(kx) \nonumber \\ &= \cfrac{2}{\pi} - \cfrac{4}{\pi} \cdot \sum^{\infty}_{k=1} \cfrac{1}{(2k-1)(2k+1)} \cdot \cos(2kx) \nonumber \\ &= \cfrac{2}{\pi} - \cfrac{4}{\pi} \cdot \left\{ \cfrac{1}{1 \cdot 3} \cdot \cos(2x) + \cfrac{1}{3 \cdot 5} \cdot \cos(4x) + \cfrac{1}{5 \cdot 7} \cdot \cos(6x) + \cdots \right\} \end{align}三角波のフーリエ級数展開
|
|---|
| 図14 今回扱う三角波 |
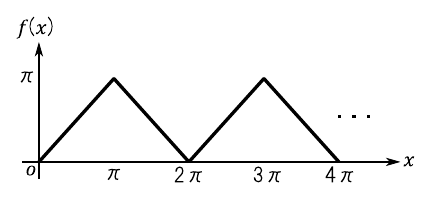
「三角波」（triangle wave）とは，図14のような波形を指します．スイッチング・コンバータなどの電源回路において，インダクタに周期の短いパルスを印加すると三角波状の電流が流れます．この波形をフーリエ級数で表してみましょう．
今回扱う三角波を次のような関数“$f(x)$”で定義します．
\begin{equation} f(x) = \left\{ \begin{array}{cc} x & (0 \leqq x < \pi) \\ -x + 2\pi & (\pi \leqq x < 2\pi) \end{array} \right. \end{equation} \begin{equation} f(x + 2\pi) = f(x) \end{equation}フーリエ係数“$a_0$”を求めます．
\begin{align} \label{eq:triangle_a0} a_0 &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} x \, dx + \cfrac{1}{\pi} \int^{2\pi}_{-\pi} -x + 2\pi \, dx \nonumber \\ &= \cfrac{1}{\pi} \left[ \cfrac{1}{2}x^2 \right]^{\pi}_{0} + \cfrac{1}{\pi} \left[ -\cfrac{1}{2}x^2 + 2\pi x \right]^{2\pi}_{\pi} \nonumber \\ &= \pi \end{align}続いて，フーリエ係数“$a_k$”を求めます．
\begin{align} a_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \cos(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} x \cdot \cos(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} (-x + 2\pi) \cdot \cos(kx) \, dx \nonumber \\ \end{align}一般に，「2つの関数の積」を積分するときは次式の「部分積分」を使います．なお，部分積分の詳細は拙著「初等関数と微分・積分」などを参照してください．
\begin{equation} \int^{b}_{a} f(x)' \cdot g(x) \, dx = \left[ f(x) \cdot g(x) \right]^{b}_{a} - \int^{b}_{a} f(x) \cdot g'(x) \, dx \end{equation}“$x \cdot \cos(kx) = x \cdot \left\{ \sin(kx)/k \right\}'$ ”であることから，部分積分を利用すると“$a_k$”を次のように計算できます．
\begin{align} a_k &= \cfrac{1}{\pi} \int^{\pi}_{0} x \cdot \cos(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} (-x + 2\pi) \cdot \cos(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \left[x \cdot \cfrac{\sin(kx)}{k} \right]^{\pi}_{0} - \cfrac{1}{\pi} \int^{\pi}_{0} \cfrac{\sin(kx)}{k} \, dx + \cfrac{1}{\pi} \left[ (-x+2\pi) \cdot \cfrac{\sin(kx)}{k} \right]^{2\pi}_{\pi} - \cfrac{1}{\pi} \int^{2\pi}_{\pi} -1 \cdot \cfrac{\sin(kx)}{k} \, dx \nonumber \\ &= 0 + \cfrac{1}{\pi} \left[ \cfrac{\cos(kx)}{k^2} \right]^{\pi}_{0} + 0 + \cfrac{1}{\pi} \left[ -\cfrac{\cos(kx)}{k^2} \right]^{2\pi}_{\pi} \nonumber \\ &=\cfrac{1}{\pi} \left\{ \cfrac{2\cos(k\pi)}{k^2} - \cfrac{2}{k^2} \right\} \end{align}ここで“$n$”を整数とすると，“$\cos(2n \cdot \pi) = 1$”および“$\cos\left\{ (2n-1)\cdot \pi \right\} = -1$”が成り立ちます．よって，次のように場合分けできます．
\begin{equation} \label{eq:triangle_ak} a_k = \left\{ \begin{array}{cc} 0 & (k = 2n) \\ -\cfrac{1}{\pi} \cdot \cfrac{4}{k^2} & (k = 2n -1) \end{array} \right. \end{equation}最後に，フーリエ係数“$b_k$”を求めます．三角波は“$f(-x) = f(x)$”を満たす「偶関数」なので“$b_k = 0$”であると考えられますが，念のため計算しておきます．
\begin{align} \label{eq:triangle_bk} b_k &= \cfrac{1}{\pi} \int^{2\pi}_{0} f(x) \cdot \sin(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \int^{\pi}_{0} x \cdot \sin(kx) \, dx + \cfrac{1}{\pi} \int^{2\pi}_{\pi} (-x + 2\pi) \cdot \sin(kx) \, dx \nonumber \\ &= \cfrac{1}{\pi} \left[ -x \cdot \cfrac{\cos(kx)}{k} \right]^{\pi}_{0} + \cfrac{1}{\pi} \int^{\pi}_{0} \cfrac{\cos(kx)}{k} \, dx + \cfrac{1}{\pi} \left[ -( -x + 2\pi ) \cdot \cfrac{\cos(kx)}{k} \right]^{2\pi}_{\pi} + \cfrac{1}{\pi} \int^{2\pi}_{\pi} -1 \cdot \cfrac{\cos(kx)}{k} \, dx \nonumber \\ &= - \cfrac{\cos(k\pi)}{k} + \cfrac{1}{\pi} \left[ \cfrac{\sin(kx)}{k^2} \right]^{\pi}_{0} + \cfrac{\cos(k\pi)}{k} - \cfrac{1}{\pi} \left[ \cfrac{\sin(kx)}{k^2} \right]^{2\pi}_{\pi} \nonumber \\ &= 0 \end{align}以上のことから，「三角波」のフーリエ級数は次のように表せます．
\begin{align} \label{eq:triangle_series} f(x) &= \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos(kx) + \sum^{\infty}_{k=1} b_k \cdot \sin(kx) \nonumber \\ &= \cfrac{\pi}{2} - \cfrac{4}{\pi} \cdot \sum^{\infty}_{k=1} \cfrac{1}{(2k-1)^2} \cdot \cos\left\{ (2k-1)x\right\} \nonumber \\ &= \cfrac{\pi}{2} - \cfrac{4}{\pi} \cdot \left\{ \cos(x) + \cfrac{1}{3^2}\cdot \cos(3x) + \cfrac{1}{5^2}\cdot \cos(5x) + \cdots \right\} \end{align}周期“$2T$”の関数のフーリエ係数
周期が“$2T$”の三角関数を考える
ここまでは，周期が“$2\pi$”である関数“$f(x)$”をフーリエ級数で表現する方法について考えてきました．しかし，周期関数の周期がいつも“$2\pi$”であるとは限りません．そこで，ここでは一般の周期“$2T$”の関数をフーリエ級数で表す方法について考えます．
|
|---|
| 図15 周期“$2T$”の$\sin$関数を考える |
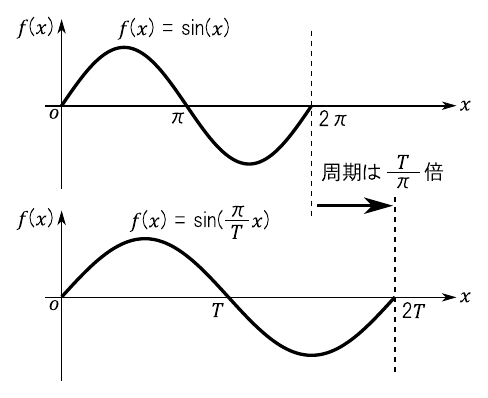
図15より，周期が“$2T$”の$\sin$波形は次式で表されます．これは，次式に“$x=2T$”を代入すると$\sin$関数の位相が“$2\pi$”になることからも納得できるかと思います．
\begin{equation} f(x) = \sin \left( \cfrac{\pi}{T} \cdot x \right) \end{equation}同様に，周期が“$2T$”の$\cos$波形は次のように表されます．
\begin{equation} f(x) = \cos \left( \cfrac{\pi}{T} \cdot x \right) \end{equation}周期が“$2T$”の関数をフーリエ級数で表す
もともと，周期“$2\pi$”の関数“$f(x)$”を表すフーリエ級数は次のとおりでした．
\begin{equation} f(x) = \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos(kx) + \sum^{\infty}_{k=1} b_k \cdot \sin(kx) \end{equation}上式は，周期が“$2\pi$”の振動成分を表す“$\cos(x)$”と“$\sin(x)$”，その2倍の（角）周波数で振動する“$\cos(2x)$”と“$\sin(2x)$”，さらに3倍の振動数をもつ“$\cos(3x)$”と“$\sin(3x)$”といった具合に，次々と細かい振動成分を加えていく形になっています．ここから類推すると，周期が“$2T$”の関数“$f(x)$”をあらわすフーリエ級数は次のようになると考えられます．
\begin{equation} f(x) = \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos\left( k \cdot \cfrac{\pi}{T} \cdot x \right) + \sum^{\infty}_{k=1} b_k \cdot \sin \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \end{equation}上式では“$\sin(\pi x/T)$”と“$\cos(\pi x / T)$”が周期“$2T$”の基本振動を表す関数であり，その2倍の（角）周波数の振動成分を表す“$\cos\left\{2 \cdot \pi x /T \right\}$”と“$\sin\left\{2 \cdot \pi x /T \right\}$”，さらに3倍の（角）周波数をもつ“$\cos\left\{3 \cdot \pi x /T \right\}$”と“$\sin\left\{3 \cdot \pi x /T \right\}$”といった成分を次々と加えていくことで周期“$2T$”の関数“$f(x)$”を表しています．
周期が“$2T$”の関数のフーリエ係数“$a_k$”
周期が“$2T$”の場合でも，フーリエ係数の求め方は周期が“$2\pi$”のときと同じです．すなわち，「所望の周期（周波数）をもつ$\cos$や$\sin$と内積をとる」という操作をすれば良いと考えられます．
まずはフーリエ係数“$a_k$”から考えます．対象とする関数“$f(x)$”と“$\cos(k \cdot \pi x/T)$”との「関数の内積」を求めると，次のようになります．ただし，今回は周期“$2T$”の関数を扱うので積分範囲を“$0 \leqq x \leqq 2T$”としています．
\begin{equation} \label{eq:ak_T_1} \left( \ f(x),\ \cos\left( k \cdot \cfrac{\pi}{T} \cdot x \right) \ \right) = \int^{2T}_{0} f(x) \cdot \cos\left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \end{equation}例によって「正規化」のための係数を求めるために，上式に“$f(x) = \cos(k \cdot \pi x /T)$”を代入して計算します．
\begin{align} \int^{2T}_{0} \cos \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \cdot \cos \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx &= \int^{2T}_{0} \cfrac{1}{2} \cdot \left\{ 1 + \cos\left( 2k \cdot \cfrac{\pi}{T} \cdot x \right) \right\} \, dx \nonumber \\ &= \cfrac{1}{2} \cdot \left[ x + \cfrac{T}{2\pi k} \cdot \sin \left( 2k \cdot \cfrac{\pi}{T} \cdot x \right) \right]^{2T}_{0} \nonumber \\ &= T \end{align}上式より，式54の両辺を“$T$”で割り算すれば係数“$a_k$”を求める式が得られます．
\begin{equation} a_k = \cfrac{1}{T} \int^{2T}_{0} f(x) \cdot \cos\left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \end{equation}周期が“$2T$”の関数のフーリエ係数“$b_k$”
続いて，フーリエ係数“$b_k$”について考えます．対象とする関数“$f(x)$”と“$\sin(k \cdot \pi x/T)$”との「関数の内積」を求めれば良いので，次のような形になります．
\begin{equation} \label{eq:bk_T_1} \left( \ f(x),\ \sin\left( k \cdot \cfrac{\pi}{T} \cdot x \right) \ \right) = \int^{2T}_{0} f(x) \cdot \sin \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \end{equation}正規化の係数を求めるために，上式において“$f(x) = \sin (k \cdot \pi x / T)$”である場合について考えます．実際に計算すると次のようになります．
\begin{align} \int^{2T}_{0} \sin \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \cdot \sin \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx &= \int^{2T}_{0} \cfrac{1}{2} \cdot \left\{ 1 - \cos\left( 2k \cdot \cfrac{\pi}{T} \cdot x \right) \right\} \, dx \nonumber \\ &= \cfrac{1}{2} \cdot \left[ x - \cfrac{T}{2\pi k} \cdot \sin \left( 2k \cdot \cfrac{\pi}{T} \cdot x \right) \right]^{2T}_{0} \nonumber \\ &= T \end{align}上式より，式57の両辺を“$T$”で割り算すれば係数“$b_k$”を求める式が得られます．
\begin{equation} b_k = \cfrac{1}{T} \int^{2T}_{0} f(x) \cdot \sin\left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \end{equation}周期が“$2T$”の関数のフーリエ係数“$a_0$”
フーリエ係数“$a_0$”を求めます．対象とする関数“$f(x)$”と“$\cos(0) = 1$”との「関数の内積」を求めれば良いので，次のような形になります．
\begin{equation} \label{eq:a0_T_1} \left( \ f(x),\ 1 \right) = \int^{2T}_{0} f(x) \cdot 1 \, dx \end{equation}正規化の係数を求めるために，上式において“$f(x) = 1$”である場合について考えます．実際に計算すると，次のようになります．
\begin{align} \int^{2T}_{0} 1 \cdot 1 \, dx &= \left[ x \right]^{2T}_{0} \nonumber \\ &= 2T \end{align}上式より，式60の両辺を“$2T$”で割り算すれば正規化できます．ただし，例によって係数“$a_k$”や“$b_k$”の式と形をそろえたいので，ここでは“$T$”で割る形で表現しておきます．後で，フーリエ級数の式で帳尻を合わせます．
\begin{equation} a_0 = \cfrac{1}{T} \int^{2T}_{0} f(x) \, dx \end{equation}周期が“$2T$”の関数のフーリエ係数のまとめ
以上のことから，周期が“$2T$”の関数“$f(x)$”を表すためのフーリエ係数は次のようにして求められます．
\begin{align} a_0 &= \cfrac{1}{T} \int^{2T}_{0} f(x) \, dx \\ a_k &= \cfrac{1}{T} \int^{2T}_{0} f(x) \cdot \cos \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \\ b_k &= \cfrac{1}{T} \int^{2T}_{0} f(x) \cdot \sin \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \end{align}上式のフーリエ係数“$a_0$”，“$a_k$”，“$b_k$”を使うと，関数“$f(x)$”を次のようにフーリエ級数で表せます．“$a_0$”だけ“1/2”倍しているのは，先ほど確認したとおり帳尻合わせをするためです．
\begin{equation} f(x) = \cfrac{a_0}{2} + \sum^{\infty}_{k=1} a_k \cdot \cos\left( k \cdot \cfrac{\pi}{T} \cdot x \right) + \sum^{\infty}_{k=1} b_k \cdot \sin \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \end{equation}周期“$2T$”の関数のフーリエ係数をマイコンで求める実験
フーリエ係数“$a_0$”および“$a_k$”を求める関数“calc_ak()”
周期“$2T$”の関数“$f(x)$”のフーリエ係数をマイコンによる数値計算で求める実験をします．まずは係数“$a_0$”と“$a_k$”について考えます．これらは次式で得られるのでした．
\begin{align} \label{eq:a_0_prog} a_0 &= \cfrac{1}{T} \int^{2T}_{0} f(x) \cdot 1 \, dx \\ \label{eq:a_k_prog} a_k &= \cfrac{1}{T} \int^{2T}_{0} f(x) \cdot \cos \left( k \cdot \cfrac{\pi}{T} \cdot x \right) \, dx \end{align}式68 に“$k=0$”を代入すると， 式67と同じ形になります．そのため，“$a_0$”および“$a_k$”は「対象のデータに対して“$\cos(k\cdot \pi x / T)$”の値を掛け算して足していく」というプログラムを書けば求められそうです．この計算を実行する関数“calc_ak()”をリスト12に示します．
|
|---|
| リスト12 フーリエ係数$a_0$および$a_k$を求める関数 |
関数“calc_ak()”の第1引数“k”はフーリエ係数“$a_k$”の添え字“k”に対応するもので，内積を計算する相手の$\cos$関数の（角）周波数を指定する値です．第2引数“data”は，関数“$f(x)$”の波形データを保存している配列の先頭のアドレスを渡します．第3引数の“data_num”は，第2引数で渡した配列データ“data”の長さです．
4行目で定義している変数“sum”は，フーリエ係数の演算結果を格納する変数です．
7行目で定義している変数“delta”は，「関数の内積」を計算するときの1ステップあたりの値（位相の分解能）です．今回は，“$2\pi/\mathrm{data_num}$”という値にしています．これは，いままで考えてきた数式でいうところの“$\pi/T$”に相当する値です（“$\mathrm{data_num}=2T$”なので“$2\pi/\mathrm{data_num} = \pi/T$”）．
10行目から始まるfor文では，変数“sum”に対して関数$f(x)$のデータ“data”と“$\cos(k\cdot \pi x /T)$”の積を次々と足し算しています．これにより，近似的に積分演算を実行しています．
16行目ではフーリエ係数を正規化するために“$1/T$”を掛け算する処理をしています．今回は“$2T=\mathrm{data_num}$”なので，“$1/T = 2/\mathrm{data_num}$”を掛け算することになります．
19行目で，計算結果として“sum”の値を返して終了です．
フーリエ係数“$b_k$”を求める関数“calc_bk()”
リスト13に，フーリエ係数“$b_k$”の値を求める関数“calc_bk()”のソース・コードを示します．基本的には関数“calc_ak()”と同じ構造ですが，12行目の積分演算で関数“$f(x)$”に“$\sin$”関数を掛け算しているところが異なります．
|
|---|
| リスト13 フーリエ係数“$b_k$”を求める関数“calc_bk()” |
フーリエ級数を求める関数“calc_series()”
関数“calc_ak()”および“calc_bk()”で求めたフーリエ係数が正しいことを確認するために，与えられたフーリエ係数を使ってフーリエ級数を求める関数も作っておきます．関数“calc_series（）”のソース・コードをリスト14に示します．
|
|---|
| リスト14 フーリエ級数を求める関数“calc_series()” |
この関数を使う場合は，あらかじめフーリエ係数“$a_0,\ a_1,\ a_2,\ \cdots$”および“$b_1,\ b_2,\ \cdots$”の値を用意しているものとします．先ほど作った“calc_ak()”や“calc_bk()”を使って求めても良いですし，自分で何か適当な値を用意しても構いません．いずれにしても，これらのフーリエ係数は何らかの配列に格納してあるものとします．
第1引数の“ak”および第2引数の“bk”は，フーリエ係数“$a_k$”および“$b_k$”を格納した配列の先頭のアドレスを渡します．今回は，これらの配列の長さは同じであるとし，この配列の長さを第3引数“coeff_num”として渡します．第4引数“data_num”は，フーリエ級数によって再構築する関数“$f(x)$”の周期（データ数）を指定します．
4行目では，計算結果として得られる関数“$f(x)$”のデータを格納するメモリ領域を“malloc()”関数で用意しています．このメモリ領域には，配列“result[]”としてアクセスできます．
7行目では，データ点数“data_num”に応じて1ステップあたりの分解能を計算しています．
10行目から13行目ではフーリエ係数“$a_{0}/2$”の値を配列“result”に加算しています．これでオフセットの情報が付加されます．
16行目から23行目では，フーリエ級数において“$a_k \cdot \cos (k \cdot \pi x/T )$”で表される振動成分を加算しています．
26行目から33行目では，フーリエ級数において“$b_k \cdot \sin (k \cdot \pi x/T )$”で表される振動成分を加算しています．
36行目から39行目では，演算結果を“printf()”関数で出力しています．
42行目では，計算結果を格納するために確保していたメモリ領域を“free()”関数で解放しています．
関数のソース・コードを記述する場所
リスト12からリスト14に示した関数“calk_ak()”，“calc_bk()”，“calc_series()”は，ソース・ファイル“main.c”の“/* USER CODE BEGIN 0 */”から“/* USER CODE END 0 */”の間に記述します．
ここまで紹介した実験をすべてやっている場合は“_write()”関数や“print_array()”関数も記述してあるので，この部分はリスト15のような状態になります．
|
|---|
| リスト15 ユーザ定義関数は“/* USER CODE BEGIN 0 */”から“/* USER CODE END 0 */”の中に書く |
矩形波のフーリエ係数をマイコンで求める
ここまでに用意した関数を使って，「矩形波」のフーリエ係数を求めてみましょう．“main()”関数の内部にある“/* USER CODE BEGIN 2*/”から“/* USER CODE END 2*/”の間に，リスト16の内容を記述します．
|
|---|
| リスト16 矩形波のフーリエ係数を求める場合のmain()関数内の記述 |
4行目では，関数“$f(x)$”を構成する波形データのデータ点数“data_num”を定義しています．今回は1000ポイントとします．
7行目では，“data_num”で指定した大きさのデータを記憶するメモリ領域（配列）を確保しています．今回扱うデータはfloat型なので，“sizeof(float) * data_num”が必要なメモリ領域のサイズとなります．
10行目から16行目で，は関数“$f(x)$”の波形データを作っています．今回は図12の矩形波（の周期を“1000”にしたもの）のデータを用意しています．
19行目から21行目では，フーリエ係数“$a_k$”および“$b_k$”の値を格納するメモリ領域を確保しています．本来のフーリエ級数は無限に続きますが，コンピュータのメモリは有限なので計算を途中で打ち切る必要があります．変数“coeff_num”は，その項数を設定するために使います．“coeff_num”を大きくするほどフーリエ級数（の近似）を表す項数が増えるので正確な値が得られますが，その分だけ計算時間が長くなります．
24行目から28行目では，“calc_ak()”関数を使ってフーリエ係数“$a_0$”および“$a_k$”を求めています．デバッグのために，各周期の係数“$a_k$”が求まるたびに“printf()”関数で表示するようにしています．
33行目から37行目では，“calc_bk()”関数を使ってフーリエ係数“$b_k$”を求めています．“$b_0$”は常に“0”になる（$\sin(0) = 0$だから）ので計算は不要ですが，配列“ak[]”と“bk[]”の長さを同じにしたいのでこのような記述にしています．
42行目では，ここまでに求めたフーリエ係数“$a_0$”，“$a_k$”，“$b_k$”にもとづいて，“calc_series()”関数でフーリエ級数を求めています．ここでは，画面上にもとの関数“$f(x)$”を再構築した値が表示されます．ここで表示される値をExcelなどでグラフ化すれば，計算が正しいことを確認できます．
45行目と46行目では，確保していたメモリ領域を念のため解放しています．
|
|---|
| 図16 「リスト16」のプログラムを実行した様子 |
パソコン側で“Tera Term”を起動してリスト16のプログラムを実行すると，図16のような結果が得られます．
先に式23および式24で求めたとおり，“$a_0$”や“$a_k$”（$k \geqq 1$）の値は“0”になっています．一部“0.004000”という値が出ていますが，これは数値計算による誤差であると考えられます．
また，式26で求めたとおり“$b_1 = 4/(1 \cdot \pi) \fallingdotseq 1.2732$”，“$b_2 = 0$”，“$b_3 = 4/(3 \cdot \pi) \fallingdotseq 0.4244$”といった値が得られています．
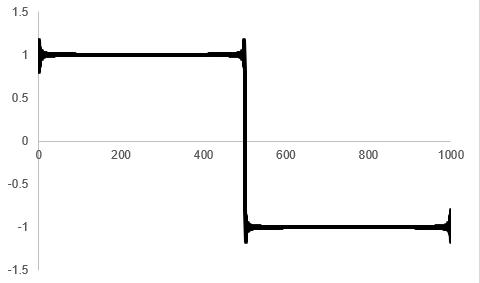
Tera Term上で[編集] - [全て選択] をクリックしてデータ全体を選択します．さらに[Ctrl] + [c] キーを押してデータをコピーして，Excelに貼り付けます．この状態で「散布図」のグラフ（直線）を描くと，図17のような結果が得られます．
|
|---|
| 図17 Tera Termの出力をExcelに貼り付けてグラフを描画した様子 |
Excelはフーリエ係数のデバッグ表示の部分（“ak[0] = 0.000”など）をグラフのタイトルして処理するので，図17のような状態になります．このタイトルを削除してグラフを整えると，図18のようになります．
|
|---|
| 図18 “coeff_num = 10”として求めた矩形波のフーリエ級数のグラフ |
図18のグラフはプログラムで“coeff_num = 10”として計算したものなので，まだ波形が矩形波に収束していません．変数“coeff_num”の値を大きくすれば理想的なフーリエ級数の形に近づきますが，それに伴い計算時間が長くなります．
変数“coeff_num”の値は，フーリエ係数“$a_k$”および“$b_k$”の添え字“k”の最大値を指定するものでした．すなわち，もとの関数“f(x)”を構成する$\sin$関数や$\cos$関数の「振動数の最大値」に相当します．今回は波形を表す配列の長さ“data_num”が“1000”なので，このデータ列が表現し得る最大の振動数は“500”となります（1点おきに“$+1$”と“$-1$”をとる波形が最大の振動数となるから）．
このあたりの議論は後で解説する「サンプリング定理」と深く関係しているのですが，今回は「変数“coeff_num”の上限は$1000 \div 2 = 500$である」ということだけ意識しておけば十分です．
“coeff_num = 400”として計算した結果を図19に示します．もとの矩形波のデータにかなり近づいていることがわかります．なお，この計算には少し時間がかかります．クロック周波数を180 MHzにしても待ち時間が発生するくらいなので，デフォルトの16 MHzだと非常に長い時間がかかります．ご注意ください．
|
|---|
| 図19 “coeff_num = 400”として求めた矩形波のフーリエ級数のグラフ |
全波整流波形のフーリエ係数をマイコンで求める
続いて，「全波整流波形」のフーリエ係数をマイコンで求めます．リスト16の9行目から16行目で矩形波を定義していた部分を，リスト17のように書き換えます．
|
|---|
| リスト17 全波整流波形を定義する |
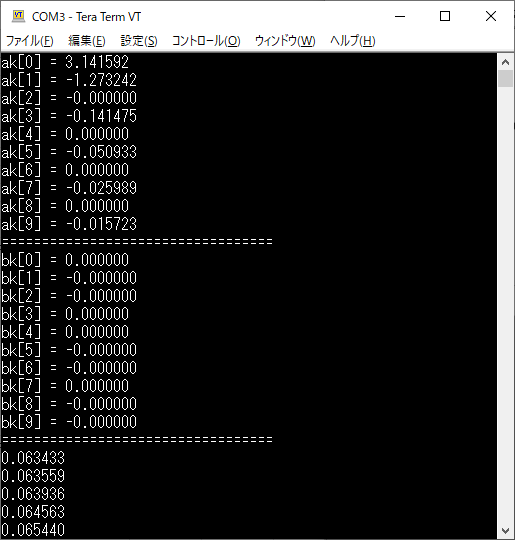
この状態で“coeff_num = 10”として計算を実行すると，図20のような結果が得られます．
|
|---|
| 図20 “coeff_num = 10”として全波整流波形のフーリエ係数を求めた様子 |
先に式30で求めたとおり“$a_0 = 4/\pi \fallingdotseq 1.2732$”となっています．また，式35で求めたとおり“$a_1 = 0$”，“$a_2 = -4/(\pi \cdot 1 \cdot 3) \fallingdotseq -0.4244$”，“$a_3 = 0$”，“$a_4 = -4/(\pi \cdot 3 \cdot 5 \fallingdotseq) -0.08488$”となっていることが確認できます．
“$b_k$”については，式39で求めたとおり“$b_k = 0$”となっています．
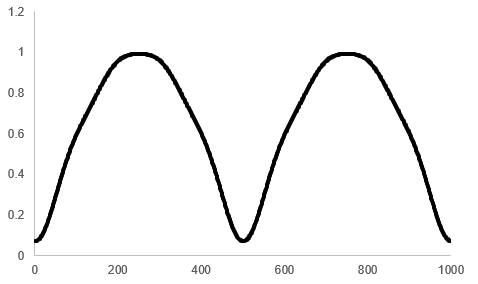
図21に“coeff_num = 10”として計算したフーリエ級数のグラフを示します．おおよそ全波整流波形になっていることはわかりますが，まだ精度が足りないようです．
|
|---|
| 図21 “coeff_num = 10”として求めた全波整流波形のフーリエ級数のグラフ |
図22に“coeff_num = 400”として計算したフーリエ級数のグラフを示します．かなり全波整流波形に近づいていることがわかります．
|
|---|
| 図22 “coeff_num = 400”として求めた全波整流波形のフーリエ級数のグラフ |
三角波のフーリエ係数をマイコンで求める
「三角波」のフーリエ係数もマイコンで計算してみましょう．リスト16の9行目から16行目の部分をリスト18のように書き換えます．
|
|---|
| リスト18 三角波を定義する |
この状態で“coeff_num = 10”として計算を実行すると，図23のような結果が得られます．
|
|---|
| 図23 “coeff_num = 10”として三角波のフーリエ係数を求めた様子 |
式43で求めたとおり“$a_0 =\pi \fallingdotseq 3.1415$”となっています．また，式47で求めたとおり“$a_1 = -4/\pi \fallingdotseq -1.2732$”，“$a_2 = 0$”，“$a_3 = -4/(\pi \cdot 3^2) \fallingdotseq -0.1414$”，“$a_4 = 0$”となっていることが確認できます．
“$b_k$”については，式48で求めた通り“$b_k = 0$”となっています．
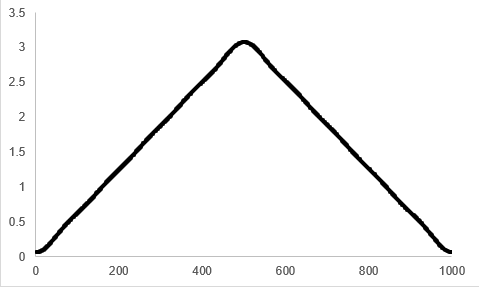
図24に，“coeff_num = 10”として計算した三角波のフーリエ級数のグラフを示します．
|
|---|
| 図24 “coeff_num = 10”として求めた三角波のフーリエ級数のグラフ |
さらに“coeff_num = 400”として計算した結果を図25に示します．
|
|---|
| 図25 “coeff_num = 400”として求めた三角波のフーリエ級数のグラフ |
“DFT”（離散フーリエ変換）と“FFT”（高速フーリエ変換）
今回は「関数“$f(x)$”と$\sin$や$\cos$との内積をとる」というアプローチでフーリエ係数を求めるプログラムを作りました．これは，ディジタル信号処理における「離散フーリエ変換」（Discrete Fourier Transform, DFT）の原始的な形であると言えます．
実際にプログラムを実行してみればわかりますが，DFTの計算にはかなり長い時間がかかります．分析対象である関数“$f(x)$”のデータ点数が多いほど，計算時間は長くなります．また，精度を上げるためにフーリエ係数の数（“coeff_num”に相当する）を増やしても計算時間の増加につながります．これでは，リアルタイム処理など不可能です．
そこで，DFTとほぼ同じ内容の計算を非常に短い時間で処理できるアルゴリズムが開発されました．これを「高速フーリエ変換」（Fast Fourier Transform: FFT）といいます．FFTを使えば，桁違いに短い時間で処理を実行することができます．実際にマイコンでフーリエ解析を行うときは，ほぼ100% FFTが使われます．
DFTやFFTのアルゴリズムの詳細は機会を追って解説します．