確率・統計処理&真値推定!
自動運転時代のカルマン・フィルタ入門
高校数学から倒立振子の設計まで!システムの数理モデルで雑音を取り除く(講義828分/697頁)
- 著者・講師: 別府 伸耕/Nobuyasu Beppu(リニア・テック)
- 企画編集・主催: ZEPエンジニアリング株式会社
- 1人当たり1ライセンスです
ご購入
下記のボタンを押して,必要事項の入力をお願いいたします.
ご購入前にご理解いただきたいこと
- 確率・統計ロボティクス学習キットも必要な場合は,[VOT/KIT]の購入をご検討ください.本製品の詳細は,z-kalman-mv2をご参照ください.
- 本VODは,2021年2月24日~27日に開催したウェビナを録画して編集した動画です.繰り返し再生,一時停止,巻き戻しが可能です.
講義内容
あらまし
本セミナの主題は,真値推定アルゴリズムの一種である「カルマン・フィルタ」を理解することです. カルマン・フィルタは,自動運転をはじめとする高精度自動制御やデータ解析の分野におけるキー・テクノロジです. 本セミナでは「倒立振子ロボット」を題材として,カルマン・フィルタの理論と実装方法を解説します.
|
|---|
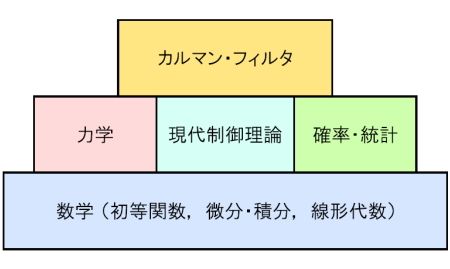
| 図1 本セミナで解説する理論の構造図 |
アジェンダ
[Part1]: イントロダクション,初等関数,微分・積分
「関数」,「微分・積分」,「線形代数」という3つの分野は,ロボット設計,ディジタル信号処理,電子回路設計など,あらゆる理工学の基礎になっています.別セミナで扱う「力学」,「現在制御理論」,「カルマン・フィルタ」,「確率・統計」という分野でも,これらの数学が役立ちます.本セミナでは,まず「初等関数」と「微分・積分」の基礎理論を丁寧に解説します.
(1)イントロダクション
- 統計学の面白さ
- 「統計的推定」を行う信号処理
(2)初等関数
- 多項式関数・有理関数
- 三角関数
- 指数関数
- 対数関数
(3)微分・積分
- 1変数関数の微分
- 1変数関数の積分
- オイラーの公式
- 2変数関数の微分
- 2変数関数の積分
- ガウス積分
[Part2]: 線形代数
本セミナでは,線形代数の基礎理論や線形システムの利点を解説します.
(1)入力・出力がある「システム」を考える
(2)線形システムの利点
(3)線形代数
- ベクトル
- 行列
- 行列式
- 行列と連立1次方程式
- 固有値と固有ベクトル
- 対称行列と2次形式
[Part3]: 力学,解析力学
力学は,初等関数,微分・積分,線形代数を使った応用例の1つです.力学を学ぶと,ロボットなどの物体の働き方を理解したり予測したりできるようになります.本セミナでは,「ニュートンの運動方程式」から,力学モデルを作るときに役立つ「ラグランジュの運動方程式」,倒立振子のモデル作成例まで,体系的にわかりやすく解説します.
(1)イントロダクション
- 「力学」のキー・ポイント
- 「運動」のとらえかた
(2)力学
- ニュートンの運動方程式
- オイラーの回転運動方程式
- 剛体の運動
- 回転座標系とコリオリカ
(3)解析力学
(4)倒立振子のモデル作成例
[Part4]: 現代制御理論
現代制御理論の特徴は,複数の値を同時に扱えることです.この複数の値を同時にフィードバックすることを「状態フィードバック」といいます.状態フィードバックで使うフィードバック・ゲインを効率良く求める手法を「最適制御」といいます.本セミナでは,システムの安定化に利用される状態フィーバックや最適制御などの制御理論を解説します.セミナで講演する状態方程式はカルマン・フィルタの理解にもつながります.
(1)現代制御理論のキー・ポイント
(2)状態方程式
(3)可制御性と可観測性
(4)安定性
(5)状態フィードバック
(6)オブザーバ
(7)最適制御
内容 (3日目) [Part5]: 確率・統計
本セミナでは,確率と統計の基礎を解説します.確率・統計はIoTセンサ・データの解析,AI,電子回路,土木・建築など多くの分野で広く活用されています.本セミナでは統計学全般で重要な役割を果たす「正規分布」をわかりやすく解説します.正規分布はカルマン・フィルタでもよく利用されており,正しい理解が大切です.
(1)確率・統計のキー・ポイント
(2)記述統計
(3)確率の基礎
(4)確率変数と確率分布
(5)2次元の確率分布
(6)正規分布
(7)中心極限定理
[Part6]: カルマン・フィルタ
無人機やロボットが目的地に向かって走行したり航行したりするには,自分自身の「位置」や「姿勢」を正確に知ることが重要です.しかし,センサによる測定値には,誤差が含まれます.カルマン・フィルタは,センサの測定値から誤差を取り除くための技術です.本セミナでは,自動運転をはじめとする高精度自動制御やデータ解析の分野におけるキー・テクノロジ「カルマン・フィルタ」の理論を基礎から解説します.本質を理解することで,カルマン・フィルタにとどまらず多岐に渡る応用力を身に着けることができます.
(1)イントロダクション
- カルマン・フィルタのキー・ポイント
- カルマン・フィルタの動作
(2)時系列データ
(3)最大事後確率推定(1変数)
(4)カルマン・フィルタの導出(1変数)
[Part7]: カルマン・フィルタとフーリエ解析の関係
フーリエ解析は,信号処理,電子回路,線形システムなどの工学分野に広く利用されている数学的手法です.本セミナでは,フーリエ解析の考え方の要点をわかりやすく解説します.
(1)「電気」に関する微分方程式:マクスウェル方程式
(2)インダクタとキャパシタの挙動
(3)交流回路理論
(4)フーリエ変換
(5)フーリエ変換と線形性
(6)「微分方程式」を「代数方程式」にする
(7)ラプラス変換
(8)z変換
受講対象
- エンジニアリングで共通して使われる「数学」を学びたい方
- ロボット制御の手法である「現代制御理論」を理解したい方
- 一般的な「モデル・ベース開発」の考え方を理解したい方
- 真値推定アルゴリズム「カルマン・フィルタ」を理解したい方
受講者が準備するもの
ノート,筆記用具など
講師紹介
略歴
- 2011年 東京工業大学 工学部 電気電子工学科 卒業
- 2013年 東京工業大学大学院 理工学研究科 電子物理工学専攻 修了
- 2013年 株式会社アドバンテスト 入社
- 2016年 株式会社村田製作所 入社
- 2019年 リニア・テック 開業
主な著書
- 電子回路のキホン 要点マスタ50,トランジスタ技術,2015年5月号,別冊付録,CQ出版社.
- 情熱のフル・ディスクリートFMラジオ,トランジスタ技術,2016年1月号 特集 第5章,CQ出版社.
- 本質理解!万能アナログ回路塾,トラジスタ技術,2017年9月号,連載,CQ出版社.
- 初等関数と微分・積分,2019年,CQ出版社.
- 月着陸船アポロに学ぶ確率統計コンピュータ,トランジスタ技術,2019年7月号 特集,CQ出版社.
- 大解剖!CPUはこうやって動いている,トランジスタ技術,2020年5月号 特集,CQ出版社.
