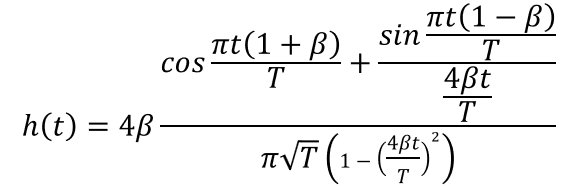高感度受信!ソフトウェア無線機の心臓部
“Root-Raised Cosine Filter”の設計
群遅延一定の狭帯域ディジタル・フィルタを送信機と受信機に実装
- 著者・講師:加藤 隆志/Takashi Kato(株式会社ラジアン)
- 企画・編集:ZEPエンジニアリング株式会社
-
[Webinar/KIT/data]Arm M4/M7/DSP×500MHz!STM32H7ハイスペック計測通信Module開発
(LIVE配信:10月26日/27日,録画受講:10月28日~31日) - 関連製品:[VOD]Linux搭載USBマルチ測定器 Analog Discovery Proで作る私の実験室
- 関連製品: [KIT]ミリ波5G対応アップ・ダウン・コンバータ MkⅡ
- 関連製品:[VOD/KIT] STM32マイコン&Wi-Fiモジュールで学ぶ C/C++プログラミング入門
- 関連製品:[VOD/KIT]初めてのソフトウェア無線&信号処理プログラミング 基礎編/応用編
- 関連製品:[VOD]Pythonで学ぶ マクスウェル方程式 【電場編】+【磁場編】
- 関連製品:[VOD]MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
- 関連記事:超長距離無線LoRaからローカル5Gまで!GNU Radio×USRPで作るソフトウェア無線機
- 関連記事:5G時代の先進ミリ波ディジタル無線実験室 [Vol.8初めての28GHzミリ波伝搬実験]
- 関連記事:実験しながら学ぶフーリエ解析とディジタル信号処理
これからの無線通信を学ぶならソフトウェア無線“SDR”(Software Defined Radio)を避けて通ることができません.
SDRには,複素演算,フィルタ処理,畳み込み演算,群遅延や位相などさまざまな信号処理の知識が必要です.これまでアナログ回路で行っていた処理をソフトウェアに置き換えていますので,それらの物理的な理解も求められるでしょう.
本稿では,SDRの通信性能のかぎを握る帯域制限フィルタ“Root Raised Cosine Filter”を紹介します.このフィルタの設計しだいで,感度や通信速度が決まります.
受信感度を決める帯域制限フィルタ
ほしいのは無数のチャネルのうちのほんの一部
無線通信はアンテナを介して空間を伝搬するさまざまな通信やノイズが混在しているため,目的の信号を分離しなくてはなりません.
そのためアンテナから入ってきた信号に対して帯域制限フィルタ(BPF)を使って目的の信号だけを取り出す必要があります.
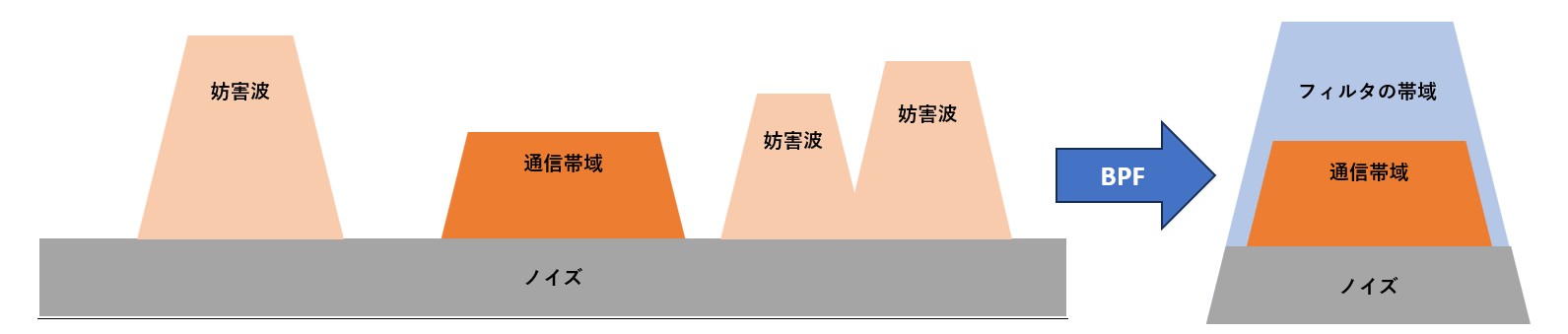
帯域を絞るほどノイズ成分が小さくなる
図1に示すように,理想的なフィルタを通過した信号は妨害波が除去され,ノイズ成分も帯域内の最低限の範囲だけに限定されます.
図1のノイズ成分の帯域を可能な限り狭くしてノイズ電力を下げ,同時に通信帯域を可能な限り削らずに残すようにすると,$S/N$,つまり受信感度が上がります.
受信感度は,ゲインが十分なら,ノイズ成分を落とすほど向上します.
従来のアナログ式帯域制限フィルタ
受信機の回路構成
図2は,従来のアナログ無線機(UHF帯,300M~3GHz)の電子回路のブロック図です.
受信感度は次の2つから求まり,計算どおりの実測値が得られます.
- 初段LNAのノイズ性能($NF$)とゲイン
- 狭帯域BPFの性能
広帯域 BPF
帯域制限用の2つのBPFがあり,前段の“Wide BPF”は,RF用の広帯域BPFです.
無線機が受信すべき全チャネルの周波数をカバーします.帯域外の強い妨害波によって,LNA(Low Noise Amplifier)がひずんで,感度が低下するのを防ぎます.
狭帯域 BPF
後段の“Narrow BPF”は,ミキサ(MIX)がRF周波数を変換して出力する固定周波数のIF(Intermediate Frequency)信号を通過させます.
1チャネル分の情報をもつ信号に帯域を絞り込む狭帯域BPFです.必要な信号を抽出できるぎりぎりの帯域をもち,余分なノイズや妨害波を可能な限りそぎ落とします.
アナログ・フィルタはディジタル通信に不向き
群遅延はディジタル波形をひずませる
「群遅延」とは,周波数に対する位相の変化を微分したものです.回路の位相変化の程度を数値で表したものです.
アナログ通信(ラジオなど)では,群遅延を気にする必要がありません.人は,周波数ごとの位相差の影響をあまり感知しないからです.
群遅延(位相遅延の周波数に対する傾き)が周波数によって変化する電子回路は,入力信号の周波数が変わると,それにともなって位相遅延の傾き(変化率)が変わります.
群遅延の大きい回路に,さまざまな周波数成分からなるステップ信号を入力すると,図3に示すように出力波形がひずみます. ステップ波形をひずませる回路は,シンボル間干渉が致命的となるディジタル通信には使えません.
実際のアナログ・フィルタの群遅延
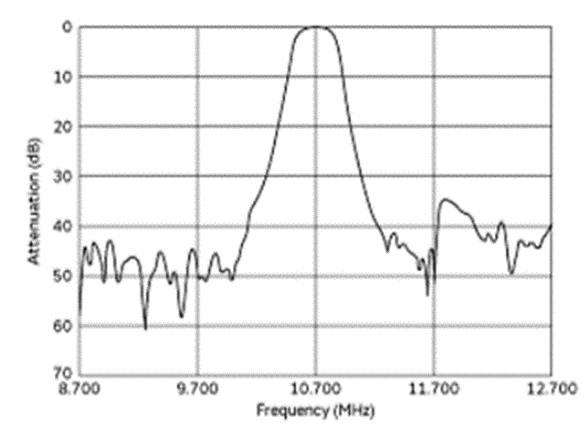
図4は,FM放送受信用の帯域$f_{BW}=300$kHzのBPFを想定した,セラミック・フィルタ(中心周波数10.7MHz)の通過特性です.
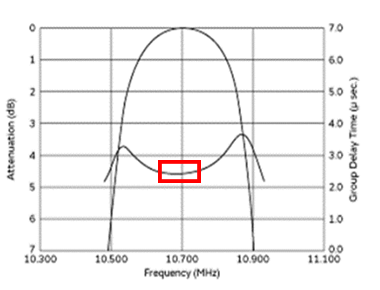
通過域に着目した図5を見ると,群遅延特性を含んでおり,特にカットオフ周波数付近で大きくなっています.
群遅延は,フィルタのカットオフ付近で大きく変化し,信号帯域が群遅延変化の大きい領域にかかると,波形がひずみます. ディジタル通信機に利用できるのは,群遅延がフラットな図5の赤枠部だけです. 群遅延の許容範囲は,採用する変調方式(BPSK,QPSK,16QAMなど)や要求される通信品質によって異なります.
ディジタルなら群遅延一定の狭帯域フィルタを作れる
IF信号をA-D変換して数値演算する
ディジタル通信機を設計するにあたり,RF部の広帯域BPFはアナログ回路で構成しても,その群遅延の影響はあまり受けません.しかし,IF段の狭帯域BPFは,群遅延が大きくなるため,ディジタル信号処理で実現するのが賢明です.
ディジタル通信機の多くは,IF信号をA-Dコンバータでディジタル信号に変換し,ソフトウェアによる数値演算でフィルタ処理しています.このような無線機を“SDR”(Software Defined Radio)または「ソフトウェア無線」と呼びます.
IIRではなく,FIRフィルタを使う
ディジタル・フィルタは,非常に柔軟に周波数特性を設計できます.アナログ・フィルタの逆の特性を実現することも可能です.
ディジタル・フィルタには次の2種類があり,ディジタル変復調では,位相直線性の確保(群遅延が一定)とシンボル間干渉の最適化のためFIRフィルタが使用されます.
FIRフィルタ
特徴は,群遅延が一定であることと,周波数特性を自由に設計できることです.また,常に動作が安定しています.
FIRフィルタは位相直線が良いので,積極的に位相をコントロールできます.たとえば,A-Dコンバータ前段のアンチエイリアス用のアナログ・フィルタで悪化した,帯域内のリプルや群遅延を補償しつつ,周波数特性をフラットにすることも可能です.
欠点は,入力から出力までの時間,つまり遅延が大きいことです.
係数は「インパルス応答」→「窓関数,周波数応答」→「IFFT」→「窓関数」という手順で求めます.
IIRフィルタ
特徴は,アナログ・フィルタと同等の特性が再現できることと,遅延が小さいことです.
欠点は,群遅延が一定でなく,設計の自由度が限定的なことです.また,発振など動作が不安定になる可能性があります.
係数は「伝達関数」→「双1次$z$変換」という手順で求めます.
ディジタル無線機の送信と受信の両方に必要な帯域制限フィルタ
1つのフィルタを2分割して
ディジタル受信機は,アナログ受信機と同様,$S/N$や選択度を上げるため,IF段に狭帯域のBPFが必須です.
またディジタル受信機は,D-Aコンバータなどを搭載するなど,高調波の発生源が多いため,送信機側に帯域制限フィルタが必須です.
1つのBPFを2分割して送信機と受信機に実装
ディジタル無線機を作るときは,「ルート・レイズド・コサイン」(RRC,Root Raised Cosine)と呼ばれるディジタル・フィルタ(以降,RRCフィルタ)を送信機と受信機それぞれに実装するのが基本です.
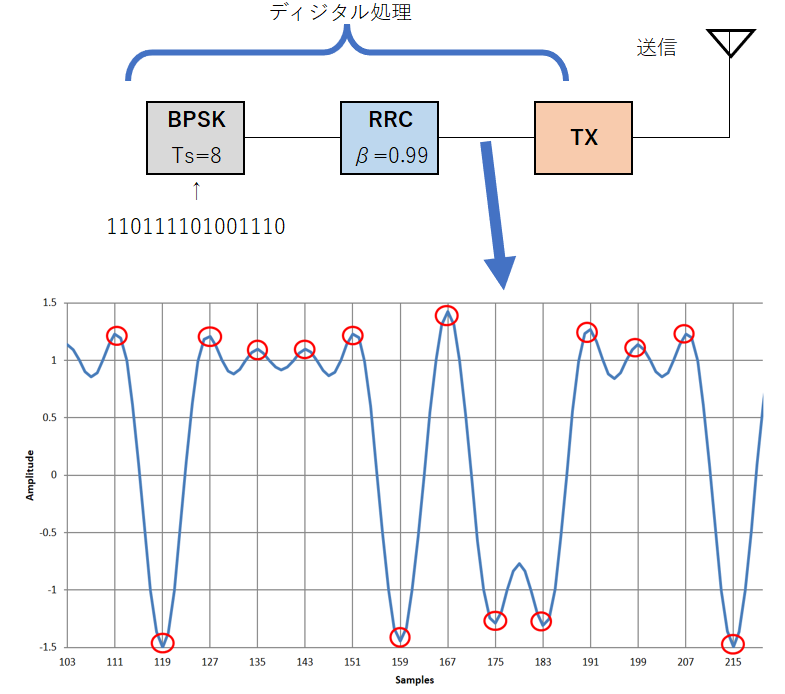
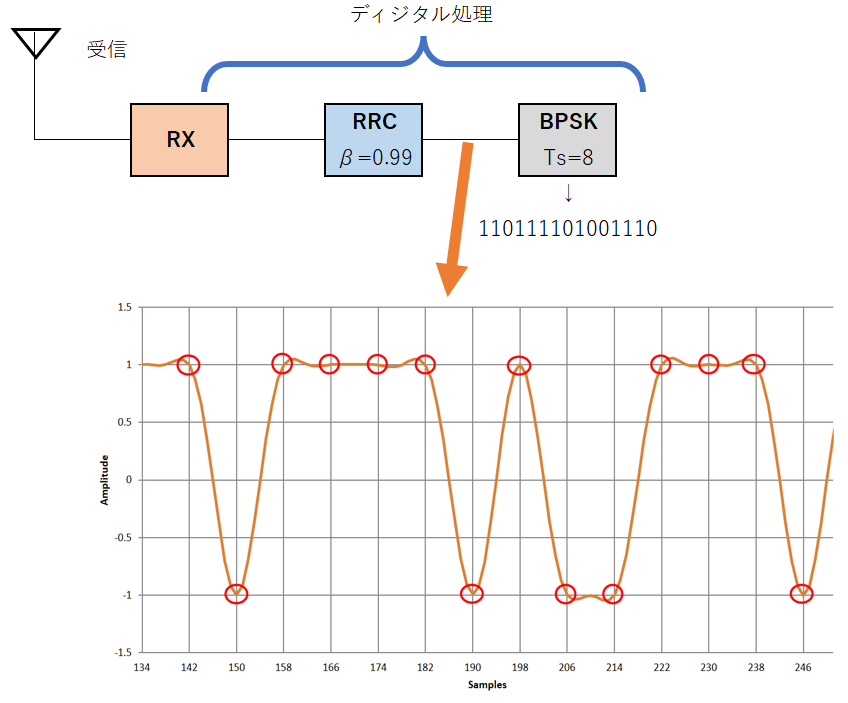
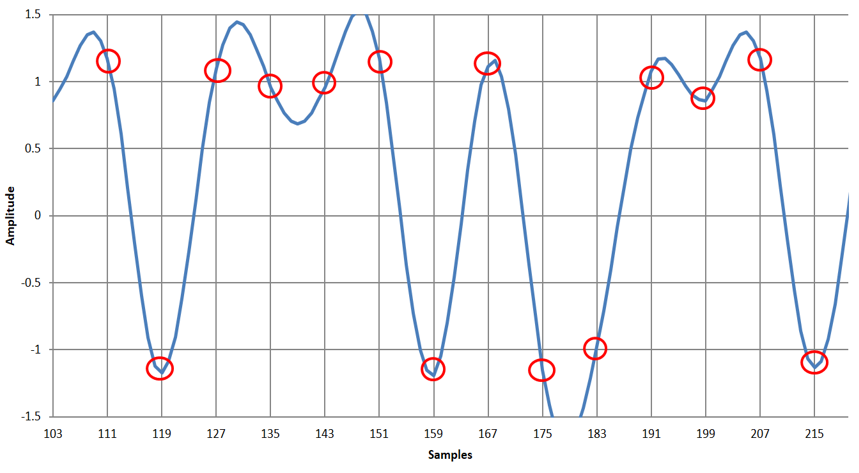
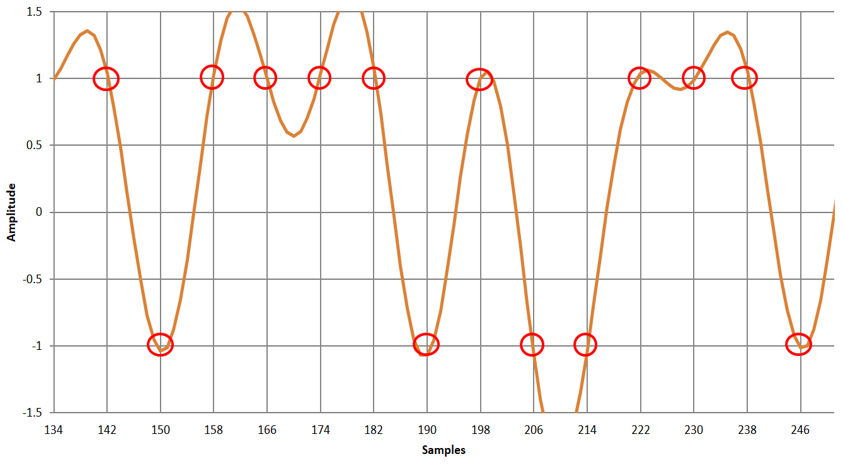
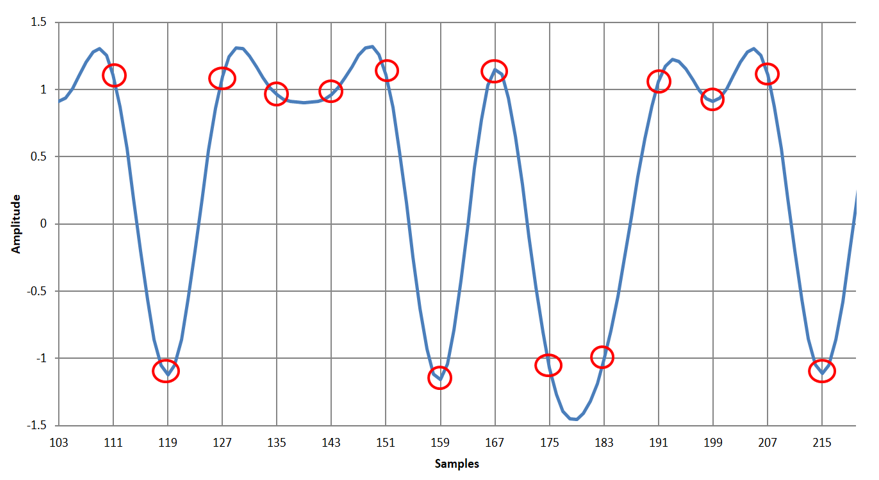
図6は,RRCフィルタを1段通過した送信機側の出力波形です.図7は,2つ目のRRCフィルタを通過した受信機側の出力波形です.ステップ応答波形が見やすいBPSK信号に対する応答も示しました.
図7に示す受信機のRRCの出力波形(赤色の丸)を見ると,きれいに$+1$と$-1$に収束しています.送受信の両方で帯域制限フィルタをかけていますが,受信出力のシンボルどうしが干渉しません.シンボル間干渉とは,前後のシンボルが影響し合うことを言います.
原理的に群遅延が一定にできないアナログ・フィルタは,ノイズや選択度を犠牲にしながら,シンボル間干渉が起きないように,帯域を広くするしか方法がありません.
RCフィルタ=RRCフィルタ $\times$ RRCフィルタ
送信機側のRRCフィルタと受信側のRRCフィルタはまったく同じものです.送信と受信の2段を通して,シンボル間干渉がゼロの完成されたBPFになります.
この完成フィルタを「レイズド・コサイン・フィルタ」(Raised Cosine Filter)と呼びます(以降,RCフィルタ).
送信機と受信機に実装するRRCフィルタの設計
STEP1:RCフィルタを設計する
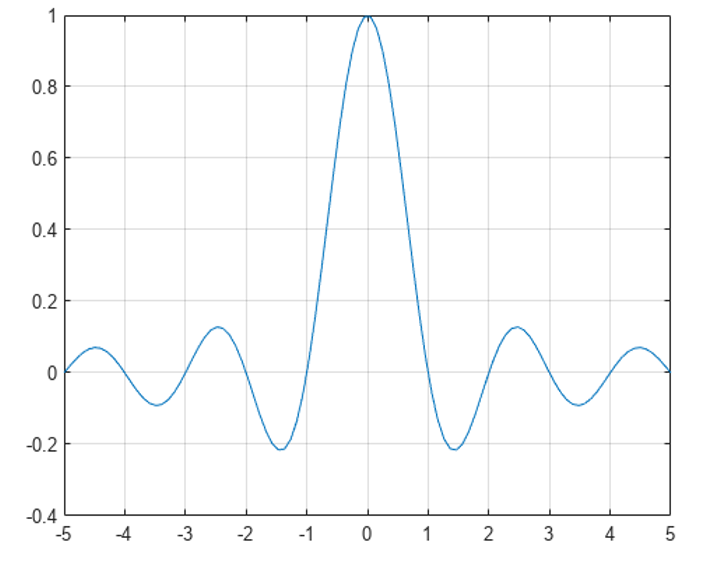
RCフィルタに,インパルス信号を入力すると,図8に示すsinc関数の波形を出力します.パルス信号を加えたときの出力を「インパルス応答」と言います.
応答がsinc関数になるフィルタは,シンボル干渉を起こしません.これに帯域制限を加えると実際のRCフィルタになります.
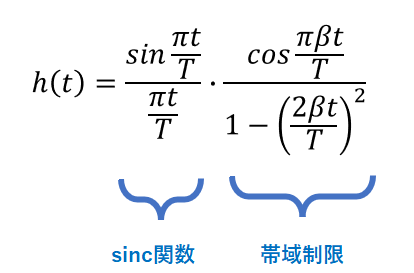
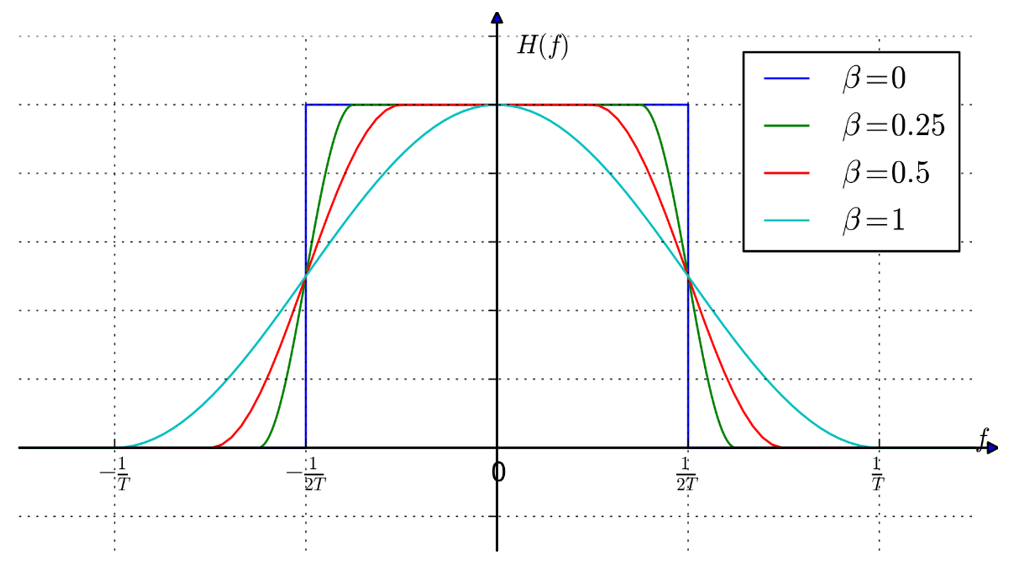
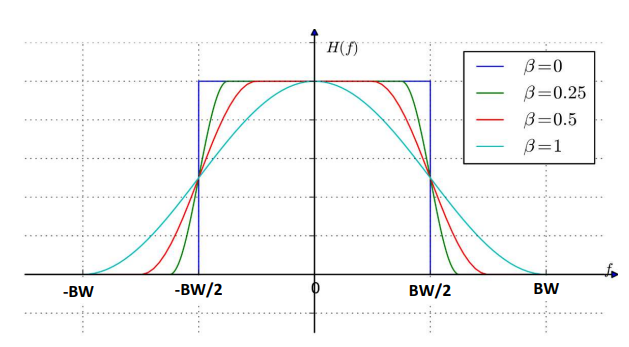
図9に示すのは,無線機に実装するRC BPFの伝達関数です.sinc関数に帯域制限の項をかけ合わせたものです. $\beta$は,帯域の広がり具合を定義する帯域制限の係数「ロールオフ率」です(図10).
ロールオフ率と帯域はトレードオフです.
図6に示すのは,$\beta$=0.99のときのシンボル収束状態です.$\beta$を大きくすると,サイズの小さい(遅延の小さい)FIRフィルタでも十分な性能が得られますが,図10のように帯域が広がります.
直線位相(群遅延一定)のフィルタのインパルス応答は左右対称です.係数のFIRフィルタの係数を調節して左右非対称にすると,位相をコントロールすることも可能です.
STEP2:RCフィルタを2分割する
RCフィルタは,同じRRCフィルタを2段直列接続したものです($RC=RRC \times RRC$).逆に,RRCフィルタは,RCフィルタを2分割したものです($RRC=\sqrt{RC}$).
図11に,RRCフィルタのインパルス応答を示します. FIRフィルタを設計する際にはこのインパルス応答をフィルタ係数とします.
STEP3 係数を決める
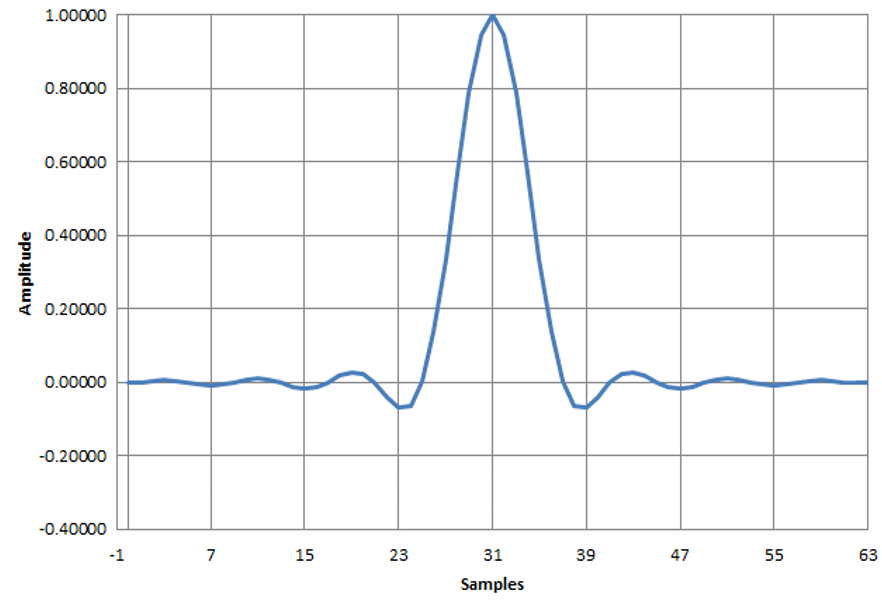
図12に示すのは,ロールオフ率 $\beta=$0.99,サンプリング・レート 8(8サンプルで1シンボル),長さ32サンプルのRRCフィルタの応答です.
図13に示すのは,フィルタの係数を決める元になるインパルス応答です.図12に,奇数対称の鏡像を追加して,線形位相が保証された長さ63サンプルの係数とします.
完成した係数(図13)は係数の長さ63でも十分に応答が収束しており,長さの短いFIRでも窓関数なしで使用可能です.
|
|---|
| 図13 $\beta=$0.99,Symbol Rate$=$8,窓関数なし($win=1.0$固定値)のRRCフィルタのFIRフィルタ係数,$\beta=$0.99, Symbol Rate$=$8) |
現実的なRRCフィルタ設計
ロールオフ率は“0.2~0.3”が適切
実際のディジタル無線機に実装される帯域制限フィルタのロールオフ率は,$\beta$=0.2~0.3です. $\beta$は小さいほど好都合です.理由は次のとおりです.
- 送信機の隣接チャネルに漏洩する電力を小さくしたい
- 受信機のノイズや隣接チャネルから受ける妨害を低減したい
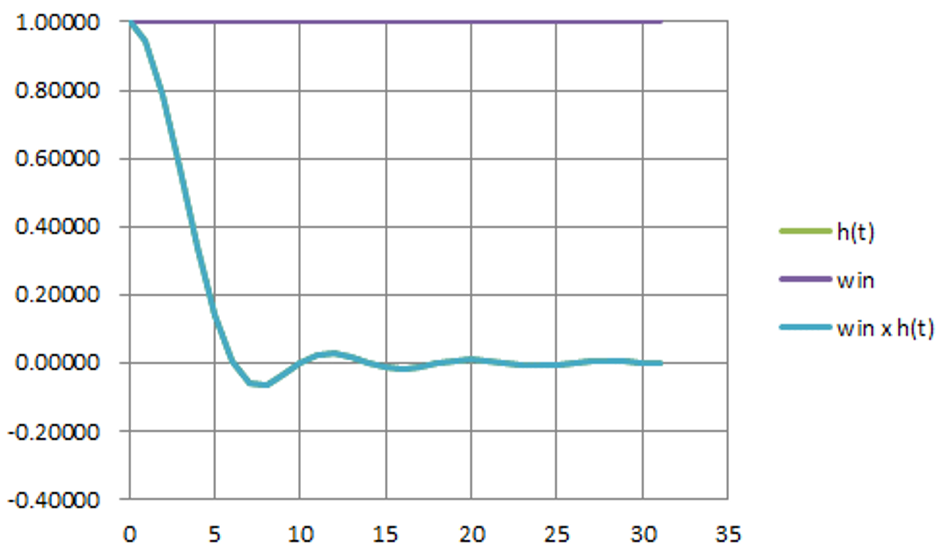
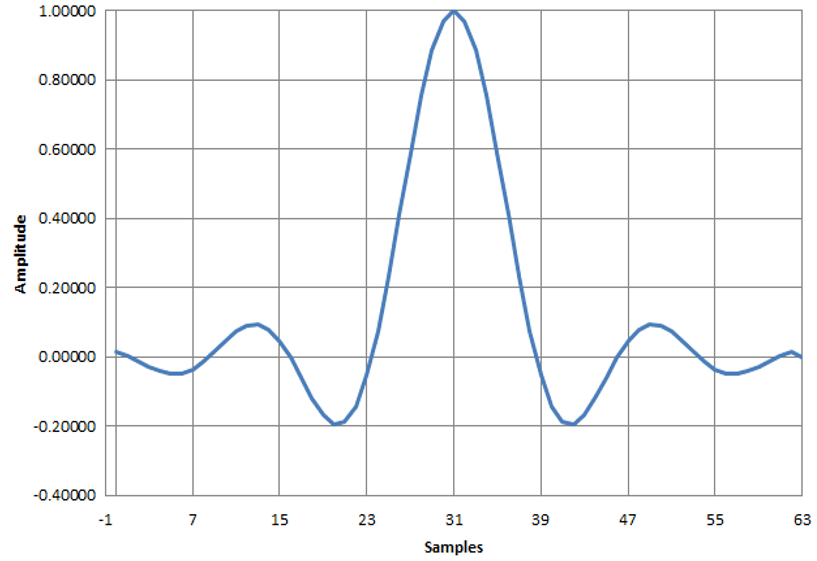
図14は,多くのディジタル無線機が採用する一般的なロールオフ率 $\beta$=0.22のときの応答です.長さ32では十分に応答が収束しきれておらず,途中で打ち切っています(図15).
|
|---|
| 図15 $\beta=0.22$,Symbol Rate$=$8,窓関数なし($win=1.0$固定値)のRRCフィルタのFIRフィルタ係数($\beta=0.22$, Symbol Rate$=$8) |
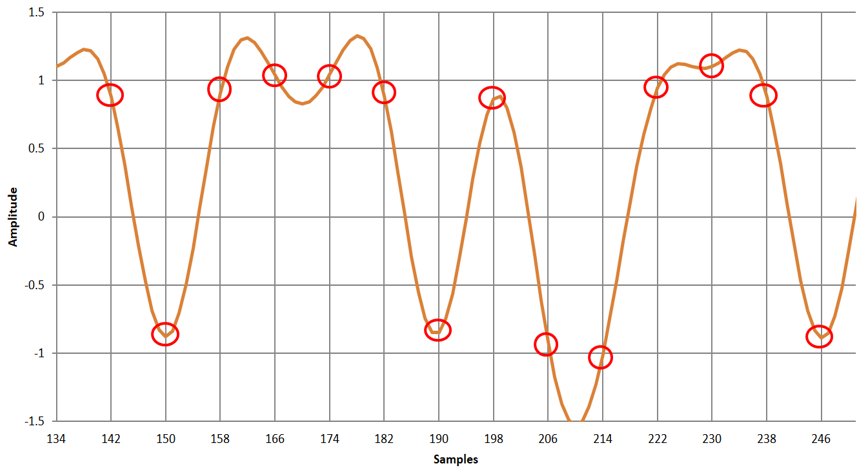
図16に,この係数を使った送信機のRRCフィルタの出力波形を示します.また,図17に,受信機のRRCフィルタの出力波形を示します.係数が収束しないうちに打ち切られますが,シンボル間干渉はあまり起こっていません.
窓関数はシンボル間干渉を悪化させることがある
無線機の設計要件から,FIRフィルタの遅延に制限があり,フィルタ係数の長さに上限がある場合は,窓関数を利用することになります.
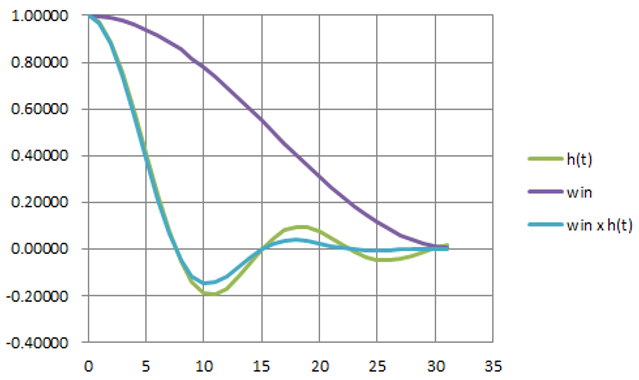
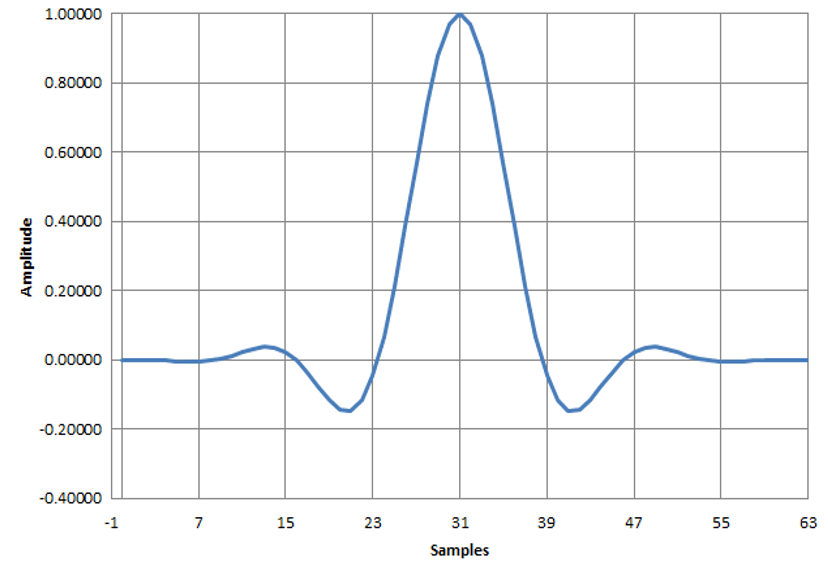
図18は,$\beta=0.22$のインパルス応答(緑色)にハン窓(紫色)をかけて得られた応答(水色)です.この応答から,FIRフィルタの係数を求めました(図19).
|
|---|
| 図19 $\beta=0.22$,Symbol Rate$=$8,窓関数使用(コサイン)のRRCフィルタのFIRフィルタ係数($\beta=0.22$,Symbol Rate$=$8,Window=cosine) |
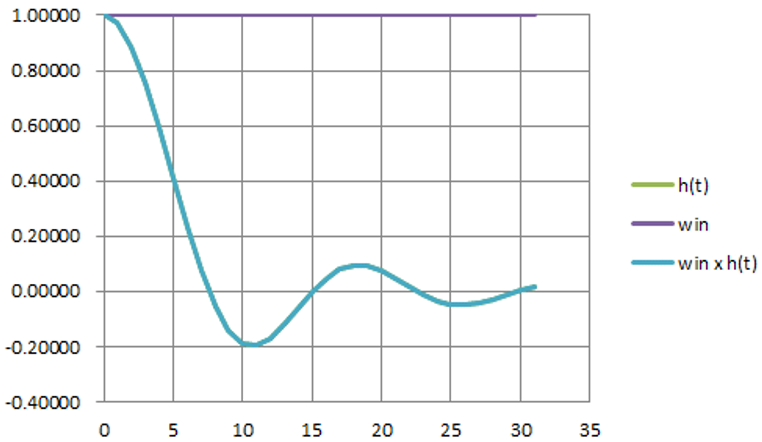
図20に示すのは,ハン窓をかけたRRCフィルタの出力波形です.図21に示すのは,同じRRCフィルタを2段通したRCフィルタの出力波形です.
窓関数を使うと,シンボル間干渉が悪化することがわかります.理想的な応答特性に対して窓関数で振幅を大きく変化させるため,当然です.
最適な窓関数の選択,収束具合によっては窓関数を使用しないなど場合に応じた対応が重要です.
コラム ビット・レートと占有帯域の関係
情報量と占有帯域幅の関係を理解することは重要です.
現代のような世界中の人類がスマホを所有する時代は,有限な資産である「周波数」をできるだけ共有するのは当たり前のことです.アナログ通信の時代は,1人当たり1チャネルで,音声帯域の通信がやっとでした(図22).
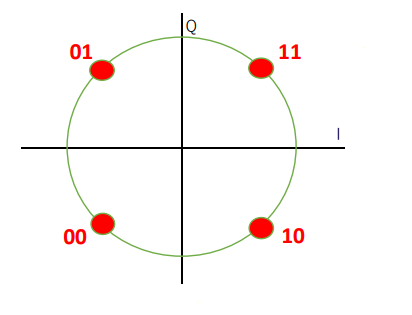
電話レベルの通話品質“AMR-NB”を用いたQPSK通信(図23)の占有周波数を算出してみましょう.
電波の状態が良ければ,16~256QAMの多値変調も利用でき,占有帯域や時間はさらに少なくなります.
\begin{align} R_S=\dfrac{R_b}{B}=\frac{4750}{2}=2375 \ symbols/s \end{align}ただし,$R_S$はシンボル・レート,$R_b$はビット・レート,$B$は1シンボルあたりのビット数です.
一般に,$R_S$の値がそのまま占有帯域とイコールです.つまり1シンボルあたり,より多値化することで帯域当たりのデータレートが増えます.
実際の無線通信機は,本稿でも紹介しているRRCフィルタを始めとする帯域制限用のロールオフ・フィルタをかけます.シンボル間干渉を発生させないように,ほとんどのディジタル無線通信機が実装しています.
この処理で帯域が広がるため,ロールオフ率$\beta$に応じて,図24のようになり,次式からQPSKで2.85kHzと求まります.
\begin{align} f_{BW}=R_S \times (1+\beta)=2375\times1.2=2.85 [\text{kHz}] \end{align}ただし,$f_{BW}$は周波数帯域,$R_S$はシンボル・レート,$\beta$はロールオフ率(ここでは0.2)です.
これは同程度の品質のアナログ通信より1桁狭い占有帯域幅です.ちなみに16QAMは16値なので,さらに1/8の帯域またはスロット時間になります(図25).
コラム 急速に進む無線通信機のソフトウェア化
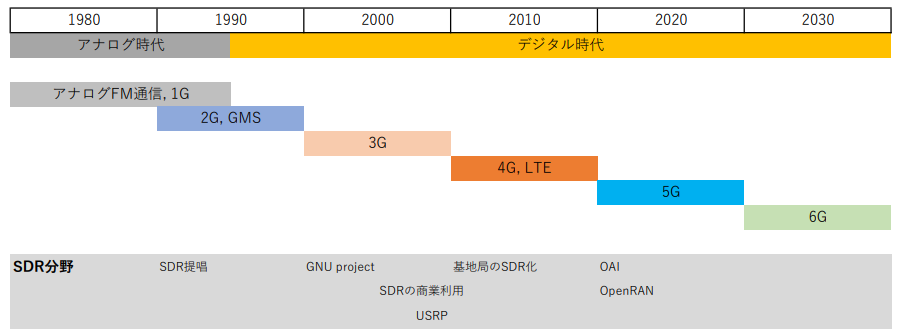
1990年代初頭,FMのアナログ無線機の開発が主流でした.この技術は戦前から50年以上と長く続くものでした.
1990年代半ばになると,ディジタル化の波が訪れ,それまでのFM技術者の淘汰,主力メーカの交代など大きなゲーム・チェンジが起こりました.
アナログ時代の無線機はRF回路とIF回路,AF回路と100$\%$アナログ技術でしたが,PLLが採用され,マイコンが内蔵されて,周波数設定もディジタル化されます.
FM変調に低速データ通信を重畳させたトランキング・システムなどを経て,90年代以降急速に通信そのものをディジタル化する流れが急速に発展し,それ以降は10年ごとに大きな技術革新の波が訪れています.
無線のディジタル化と並行して演算装置の速度が向上し,ハードウェア主体の信号処理がソフトウェアに移行しています.これが無線のSDR(Software Defined Radio)化です(図26).