[技術解説]
5G時代の先進ミリ波ディジタル無線実験室
[Vol.2 反射の起こらない線路を作る]

次世代高速移動通信と高分解能レーダのキー・テクノロジ

• 著者・講師：株式会社ラジアン（加藤 隆志/Takashi Katou）
• 企画編集・主催： ZEPエンジニアリング株式会社


• 関連製品：［KIT］ミリ波5G対応アップ・ダウン・コンバータ MkⅡ（mz-mmcon1後継機）
• 関連製品：［KIT］ミリ波5G対応アップ：ダウン・コンバータ（生産終了品）
• 関連製品：［KIT］実験用800M～6GHz 広帯域90°ハイブリッド
• 関連製品：［KIT］実験用27.5G-29.5GHzバンド・パス・フィルタ
• 関連製品：［KIT］実験用28GHzミリ波パッチ・アンテナ
• 関連製品：［VOD/KIT］GPSクロック・ジッタ・クリーナ
• 関連製品：［VOD］MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
• 関連製品：［VOD/KIT］3GHzネットアナ付き！RF回路シミュレーション＆設計・測定入門
• 関連製品：［VOD/KIT］3GHzネットアナ付き！初めてのIoT向け基板アンテナ設計
• 関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング 基礎編/応用編
• 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
• 関連記事：超長距離無線LoRaからローカル5Gまで！GNU Radio×USRPで作るソフトウェア無線機

【Index】

• Vol.1　ミリ波の性質と広帯域通信の実験環境
• Vol.2　反射の起こらない線路を作る
• Vol.3　電磁波の漏れが少ない伝送線路
• Vol.4　信号が減衰しない基板
• Vol.5　高周波センスを磨く！スミス・チャート
• Vol.6　部品や伝送線路の入出力特性モデル「$S$パラメータ」
• Vol.7　高速データ伝送 成功の鍵「群遅延」
• Vol.8　初めての28GHzミリ波伝搬実験
• Vol.9　帯域優先？精度優先？2種類の周波数変換方式

超低$C/N$！mz-mmcon1 後継機 z-mmcon2 誕生

写真Aに示すのは，1台でミリ波を使ったディジタル無線通信が可能な$I/Q$変調＆周波数コンバータ“z-mmcon2”(開発：ラジアン)です．ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1の後継機です．

スペック

1. 送信周波数範囲：24.0G～44.0GHz
2. 送信出力範囲：+10～-29dBm（信号の条件 CW）
3. 送信ゲイン範囲：+20～-19dB（$I/Q$動作時）
4. 受信周波数範囲：24.0G～44.0GHz
5. 受信入力範囲-：10dBm以下（信号の条件 CW）
6. 受信ゲイン範囲：+12～-9dB（$I/Q$動作時）
7. 受信雑音指数：10dB以下
8. ベースバンド周波数範囲：DC～100kHz（内蔵D-Aコンバータ，外部アクセス不可）
9. ベースバンド・レベル範囲：0dBm以下（内蔵D-Aコンバータ，外部アクセス不可）
10. IF周波数範囲：1G～6GHz（本体背面のSMA端子）
11. IFレベル範囲：0dBm以下（本体背面のSMA端子）
12. 電源：付属のACアダプタ（DC6V，2A）
13. 消費電流：1.5A（通常動作時）
14. 基板サイズ：128×93×1.6mm（基材はRogers4350B）
15. ケース・サイズ：$W$=140mm $D$=129mm $H$=40mm（フランジ含む）

従来品 ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1からの改善点

z-mmcon2（写真A ）は，従来機のmz-mmcon1から，下記の点が改良されています．

1. 周波数範囲の拡大（27GHz～43GHz → 24GHz～44GHz）
2. シンセサイザICの変更（ADF4372）に伴う$C/N$の大幅改善
3. 制御をWindowsアプリからターミナルに変更（FTDIドライバに起因するトラブル回避）
4. 外部機器との接続をIF（1G～6GHz）だけに変更
5. 放熱ケース採用とファンレス化，ケースの大型化
6. USBマイクロをUSB-Bに変更（コネクタ破壊対策）

あなたの知らない超高周波「ミリ波」の世界へ

本技術解説シリーズでは，ミリ波通信実験用アップ・ダウン・コンバータ MZ-mmCon1(後出のコラム参照)を題材に，$27\mathrm{G}～40\mathrm{GHz}$の超高周波「ミリ波」を確実に伝送するプリント基板の作り方を説明しています．今回(Vol.2)は，ミリ波信号を確実に伝えるための第一歩として，反射のない伝送線路を作るために高周波屋が使う「特性インピーダンス」を学びます．〈ZEPマガジン編集部〉

はじめの一歩「反射」をなくす

ビデオ信号など，アナログ信号の周波数が$100\mathrm{MHz}$前後まで高まると，絶縁体をはさんで隣り合う配線間を信号が混入する現象「クロストーク」など，さまざまなノイズになやまされます．

$300\mathrm{MHz}$以上になると，受信端で信号が跳ね返って送信単に向かって戻っていく現象「反射」が顕在化します．伝送線路の特性インピーダンスを計算で求め，反射を抑える「マッチング」の技術がが重要になります．

1GHzを超えると，信号の波長が基板のサイズぐらい(30cmほど)になり，プリント・パターンはもとより，数$\mathrm{GHz}$になるとコネクタや部品の物理形状も特性に効いてくるようになります．汎用材「FR-4」を使ったプリント基板では信号が大きく減衰するため，パナソニック社のMEGTRONやRogers社のRO4000シリーズなどの誘電損失 $\tan{\delta}$(タンデルと呼ぶ)の低い特殊材を使います．

つなぐだけでは伝わらない

ミリ波用プリント基板設計の第1歩は，「反射」の起こらない伝送線路を作ることです．

反射というのは，信号源から出力され受信端に到着した信号が跳ね返って信号の波形を乱す現象です．これを抑えこまないと，信号が減衰したり，送受信端の双方で永久に反射が繰り返されて定在波が発生することがあり，周波数によっては信号が弱まったり消えてしまったりします．

こんな現象は，低周波のアナログ信号や低速のディジタル信号で問題になることはあまりありません．

DCで$0\mathrm{Ω}$の線路でも交流では特定のインピーダンスを示す

反射は，次の3つの特性インピーダンス(電圧の瞬間的な変化に対する電流の応答のこと)をそろえることで発生しなくなります．

1. 送信回路の出力インピーダンス
2. 受信回路の入力インピーダンス
3. 伝送線路の特性インピーダンス

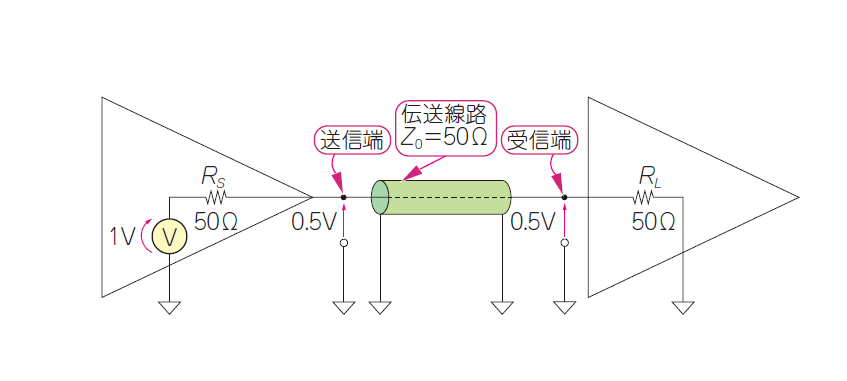
図1に示すのは，3つの特性インピーダンスがどれも$50\mathrm{Ω}$の理想的な伝送線路です．どんなに周波数が高くなっても$50\mathrm{Ω}$のままで，確実に信号が次段に伝わります．どんな伝送線路も，固有の特性インピーダンスをもっており，ゼロや無限大は存在しません．特性インピーダンスについては後で詳しく解説します．

特性インピーダンスを無視した回路は高周波で動かない

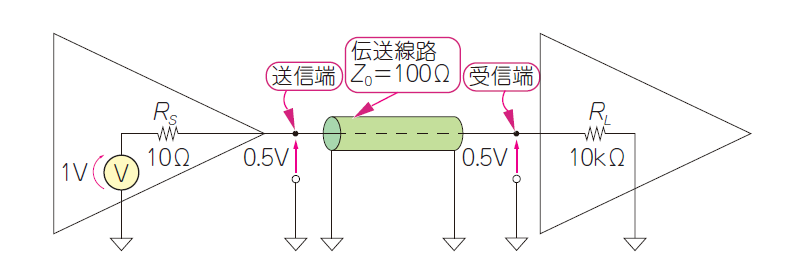
図2に示すのは，低周波のアナログ回路や低速のディジタル回路を設計している方におなじみの2つの回路が配線(プリント・パターンやケーブル)で縦続接続されたシステムです．

送信回路(OPアンプやCMOSドライバ)と受信回路を設計するときは，出力インピーダンスと入力インピーダンスを考慮するでしょう．例えば，送信回路の出力電圧と受信回路の入力電圧ができるだけ等しくなるように，送信回路の出力インピーダンスは$10\mathrm{Ω}$程度に低くしています．受信側はハイ・インピーダンス($10\mathrm{k}～100\mathrm{kΩ}$)にして，消費電力や発熱を小さく抑えます．

しかし，送信回路と受信回路をつなぐ配線(伝送線路)の特性を気にすることはあまりしません．場合によっては，実装スペースを気にして，特性インピーダンスが$100\mathrm{Ω}$以上もある幅の狭いプリント・パターンでつなぐこともあるでしょう．

このようなシステムは，回路の動作周波数が低速(数十$\mathrm{MHz}$以下)で，伝送線路が$10\mathrm{cm}$以下ならば問題ありませんが．$100\mathrm{MHz}$以上になると動かなくなる場合があります．これは，上記(1)～(3)の特性インピーダンスが等しくない「マッチング不良」になっており，信号が弱くなったり波形が乱れたりしているからです．「回路は変えていないのにプリント・パターンを少し変えたら動かなくなった」とか，「わずかな部品定数のばらつきや温度変化で市場トラブルに見舞われた」といった残念なトラブルに見舞われることになるでしょう．

高周波の世界では「時間」も考える

低周波では線路の特性インピーダンスはほぼ無視できる

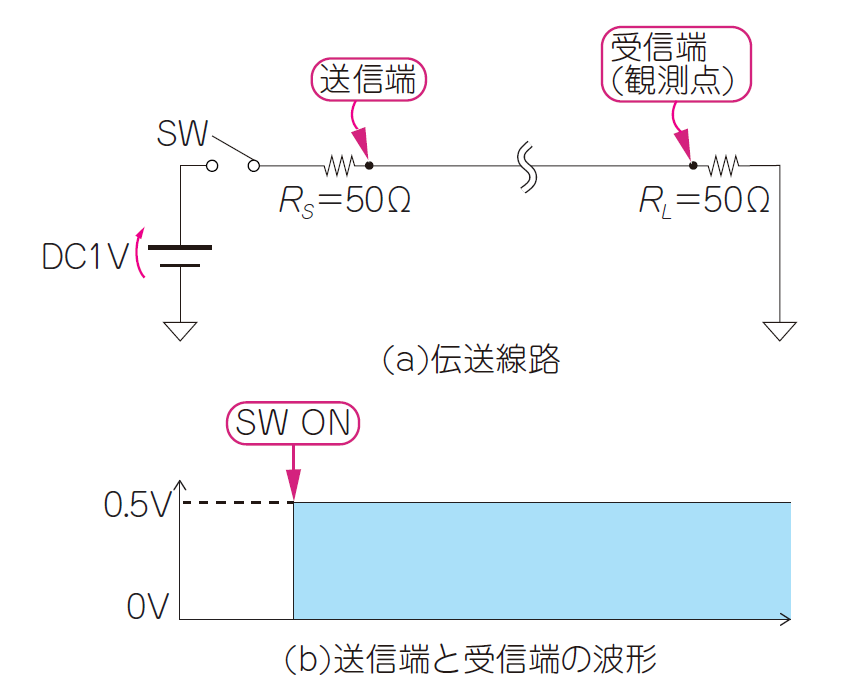
図3に示すのは，低周波の目で見たときの，スイッチ(SW)がONしたことを配線を通じて受信端の抵抗$R_L$に伝える回路です．信号源インピーダンスは$50\mathrm{Ω}$，負荷インピーダンスも$50\mathrm{Ω}$です．SW ONすると同時に観測点の電圧は2つの$50\mathrm{Ω}$で分圧された$0.5\mathrm{V}$になります．

このように低周波では，送信端の抵抗$R_S$と受信端の抵抗$R_L$の間の配線は，信号に影響を及ぼしません．回路図に伝送線路を描く必要もありません．

高周波では線路の特性インピーダンスが無視できず部品として扱う

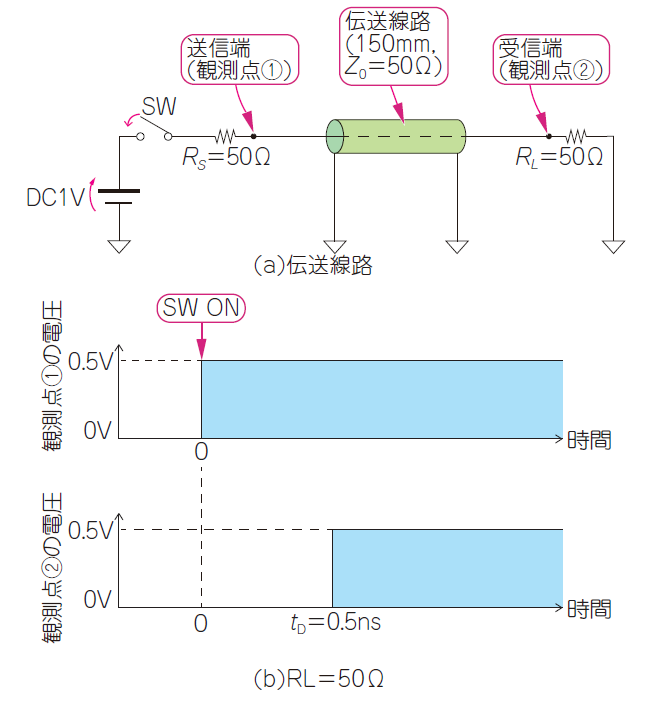
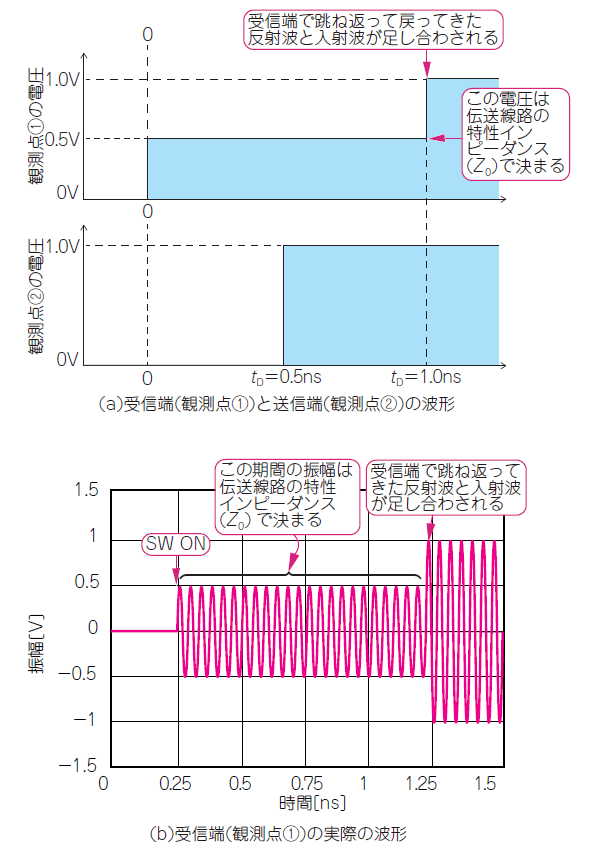
図4(a)に示すのは，観測点①(送信端)と観測点②(受信端)を長さ$150\mathrm{mm}$の線路で結んだ伝送回路です．

高周波の目で見るときは，信号が伝送線路を伝わる時間(または速度)も考えます．計算で求めると，電磁気の速度から$0.5\mathrm{ns}$です．観測点②(受信端)の電圧は，SWをONした直後から$0.5\mathrm{ns}$後，$0.5\mathrm{V}$になります[図4(b)]．では，SW ONにした直後，0.000000…1秒後，観測点①の電圧は何Vになるでしょうか？

最終的に$0.5\mathrm{V}$になるのはわかりますが，SW ONした直後は，電流は送信端($R_L$)に到達していませんから，観測点①の電圧は確定しないことになりますが，実際には伝送線路のインピーダンス(特性インピーダンス $Z_0=50\mathrm{Ω}$)によって電圧は確定します．つまり，SW ON直後，観測点①の電圧は，信号源の電圧$1\mathrm{V}$が，$R_{S}(50\mathrm{Ω}$)と伝送線路の特性インピーダンス($50\mathrm{Ω}$)によって分圧されて$0.5\mathrm{V}$になります．

反射が起きる伝送線路の波形

送信端は$50\mathrm{Ω}$，受信端は開放のとき

$R_L=\infty$(無限大)の場合はどうなるでしょうか？

図5に示すのは，送信端と伝送線路の特性インピーダンスが$50\mathrm{Ω}$で一致していますが，受信端は開放されていて伝送線路とインピーダンスが一致していません．伝送線路を流れる電流は，受信端に達するとその先行き場がありません．電流の大きさは次式から$10\mathrm{mA}$です．

図5(a)に，送信端(観測点①)と受信端(観測点v②)の電圧の変化を示します．$1\mathrm{ns}$後，送信端(観測点①)の電圧は，入力信号($0.5\mathrm{V}$)と反射して戻って来た信号($0.5\mathrm{V}$)が加算されて$1\mathrm{V}$になり，その電圧で落ち着きます．

図5(b)に示すのは，信号源が交流(AC)のときの送信端(観測点①)の波形です．信号源が直流(DC)のときと同様に，SWをONして$1\mathrm{ns}$後に，振幅が$0.5\mathrm{V}$から$1 \mathrm{V}$に変化しています．

低速ディジタル回路でも，実際は反射は起きていますが，波形の立ち上がりが遅いために，変化がわずかで見えないだけです．線路を波長に対して極端に長くすると(数$\mathrm{km}$など)，反射の影響が見えてきます．つまり，伝送線路の長さと信号の波長の関係で，反射の影響が現れたり，現れなかったりするわけで，周波数は本質的には関係がありません．

送信端も受信端も$50\mathrm{Ω}$でないとき

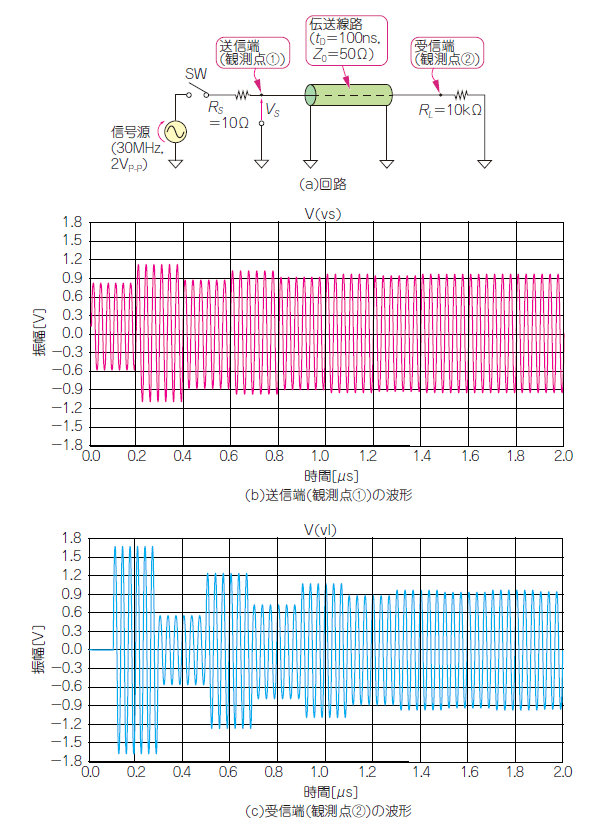
図6(a)に示すのは，受信端だけでなく，送信端の特性インピーダンスも伝送線路の特性インピーダンス($50\mathrm{Ω}$)と一致していない回路です．この回路は，受信端(負荷側)でも送信端(信号源側)でもエネルギが吸収されないので，伝送線路内で反射が繰り返される「多重反射」が発生します．

図6(b)と(c)に示すのは，送信端(信号源側)と受信端(負荷側)の波形です．特に図(b)の負荷側の波形は，伝送線路($50\mathrm{Ω}$)と負荷抵抗($10\mathrm{kΩ}$)のインピーダンス差が大きいため，信号源の倍近い電圧まで上昇しています．

送信端も受信端も，時間の経過とともに，反射を繰り返しながら振幅は$1\mathrm{V}$に収束します．

多重反射の弊害「定在波」

多重反射の往復周期は伝送線路の長さで決まります．これが入力信号の周期と一致すると定在波が発生します．

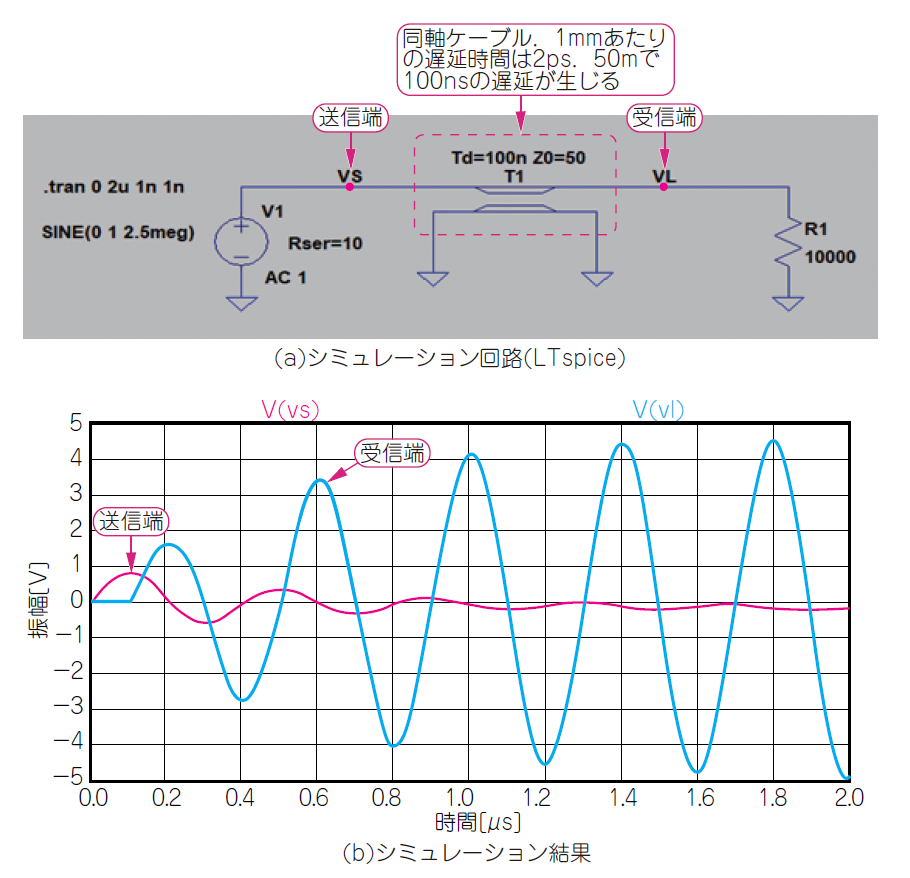
図7に示すのは，図6に示す伝送線路(伝搬時間$100\mathrm{ns}$)の信号源の周波数を$2.5\mathrm{MHz}$にしたときの送信端(観測点①)と受信端(観測点②)の波形です．$1\mathrm{V}$を入力すると，送信端の振幅は徐々に増して$5\mathrm{V}$に達します．送信端の振幅($V_S$)は時間の経過とともに消失しています．伝搬遅延時間が$100\mathrm{ns}$の同軸ケーブルの長さは$50\mathrm{m}$です．周波数が$500\mathrm{MHz}$より高くなると，1辺$30\mathrm{cm}$程度のプリント基板でも同じ現象が起こります．この現象が起きると，エネルギが長時間，伝送線路内に保持されて振動が続きます．

図7に示すように，定在波が発生しているときは，節と腹の部分で大きく振幅が異なり，節の部分に接続された受信回路は信号が消失して動作しなくなります．

数$\mathrm{GHz}$のマイクロ波以上になると，グラウンド・パターンでも共振が起こり，近くを通る伝送線路の信号が消えたり，ノイズが乗ったりするトラブルに見舞われます．とてもやっかいな現象ですが，発生のメカニズムがわかれば確実に回避できます．メカニズムを理解しないまま，電磁界シミュレータによるカット&トライだけで伝送線路を設計すると，多重反射の発生を見逃すことがあるでしょう．

特性インピーダンスの計算式

プリント・パターンの幅とグラウンド層までの距離で決まる

以上のように，高周波信号を扱う基板は，反射が起こらないように，プリント・パターンの特性インピーダンスをコントロールして設計するのが定石です．では，特性インピーダンスを決める要素は何になるのでしょうか．

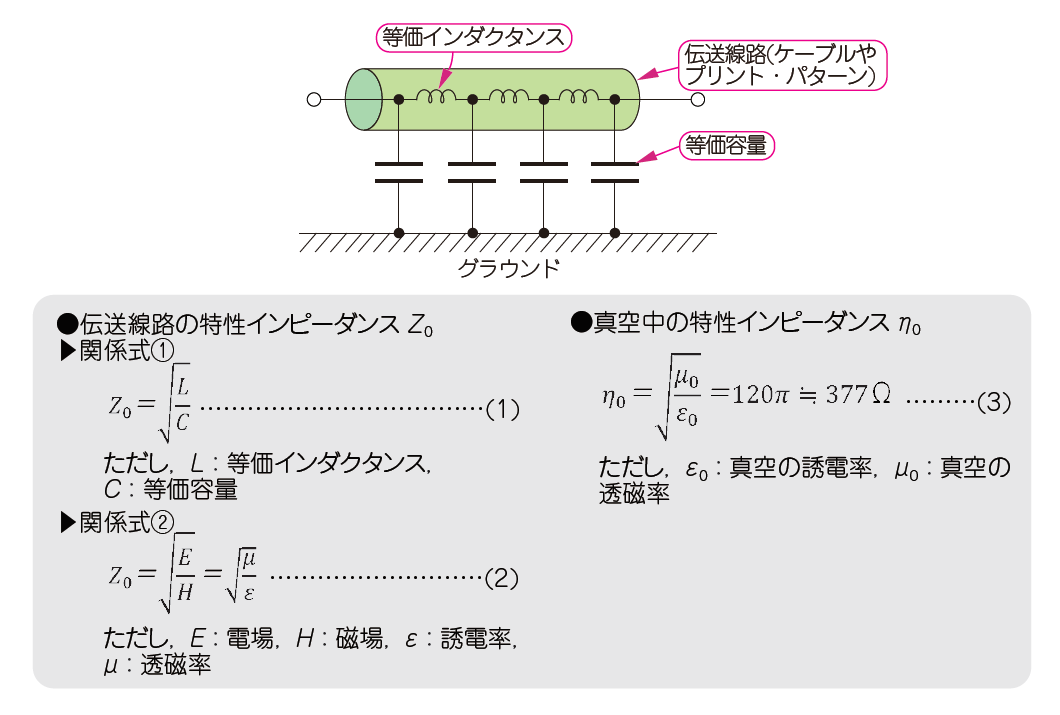
図8に示すのは，インダクタ($L$)とコンデンサ($C$)で表現した伝送線路の等価回路です．直列にインダクタ($L$)を，対グラウンドにコンデンサ($C$)が配置されています．インダクタ($L$)は，線路長で決まるパラメータです．設計で調整できるのはコンデンサ($C$)です．コンデンサ($C$)は，伝送線路であるプリント・パターンの幅と，プリント・パターンとグラウンド層の距離から設計できます．

図8の式(1)からわかるように，特性インピーダンスはインダクタ($L$)とコンデンサ($C$)の比率で決まります．プリント・パターンの幅を大きくすると，コンデンサ($C$)が大きくなって，特性インピーダンスは低くなります．

式(2)からわかるように，特性インピーダンスは，誘電率と透磁率の比からも求まります．

真空の特性インピーダンス

式(3)に示すのは，真空の特性インピーダンス($\eta_0$)を求める式です．透磁率と誘電率は定数で，$\eta_0=377\mathrm{Ω}$が得られます．これは電磁波の特性インピーダンスとして知られています．定数$\eta_0$は，さまざまな伝送線路の特性インピーダンスを計算するときに，近似式の定数として利用されます．

伝送ロスに関するパラメータ

周波数が高くなってくると，次の2つのロスが無視できなくなり，信号の振幅が弱まって波形が減衰したり鈍ったりします．

• 表皮効果による損失「銅損」
• 誘電体による損失「誘電損」

これらは，図8に示す等価回路で表すと，インダクタ($L$)と直列に銅損が，コンデンサ($C$)と直列に誘電損が入ります．

3大伝送線路の特性インピーダンスと伝搬速度

伝送線路の特性は，次の2つのパラメータで評価することができます．

1. 特性インピーダンス
2. 伝搬速度
3. ロス(減衰)

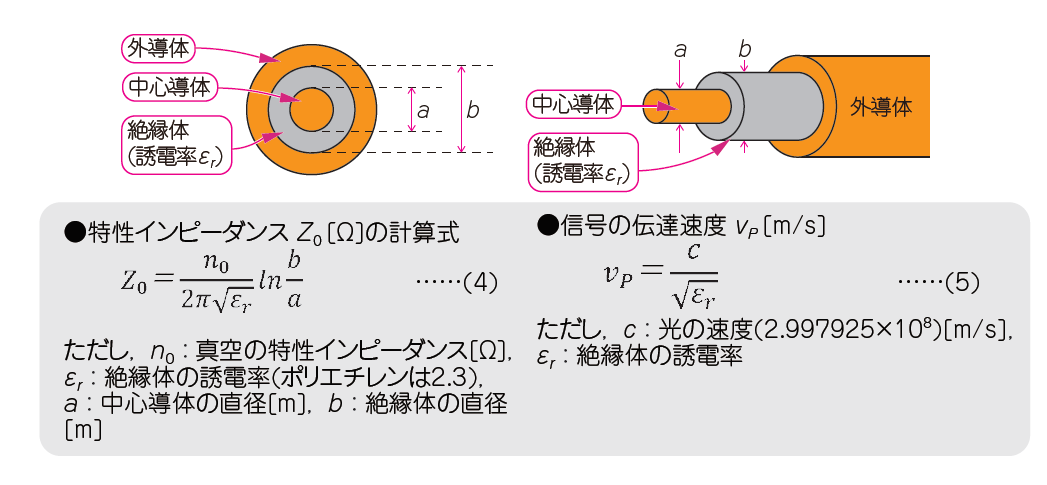
①同軸ケーブル

図8の式(1)のインダクタ($L$)とコンデンサ($C$)を直接求めるのは面倒です．通常は，図9の式(4)に示す近似式を利用して，同軸ケーブルの特性インピーダンスを求めます．同軸ケーブルは形状がシンプルなため，近似式も簡単です．

式(5)は，同軸ケーブル内を流れる信号の速度を求める式です．この式を使って伝送線路内の波長を求め，定在波の大きさを算出したり，インピーダンス・マッチングをしたりします．式がシンプルなのは，電界が分布するのは誘電体の中だけに存在するからです．

同軸ケーブルの多くは，絶縁体に誘電率($\varepsilon_r$)が$2.3$のポリエチレンを使っています．$\sqrt{2.3} \approx 1.5$ですから，同軸ケーブル内の信号の波長は，空気中での波長の$66\%$に短くなります．このレートを波長短縮率と言います．

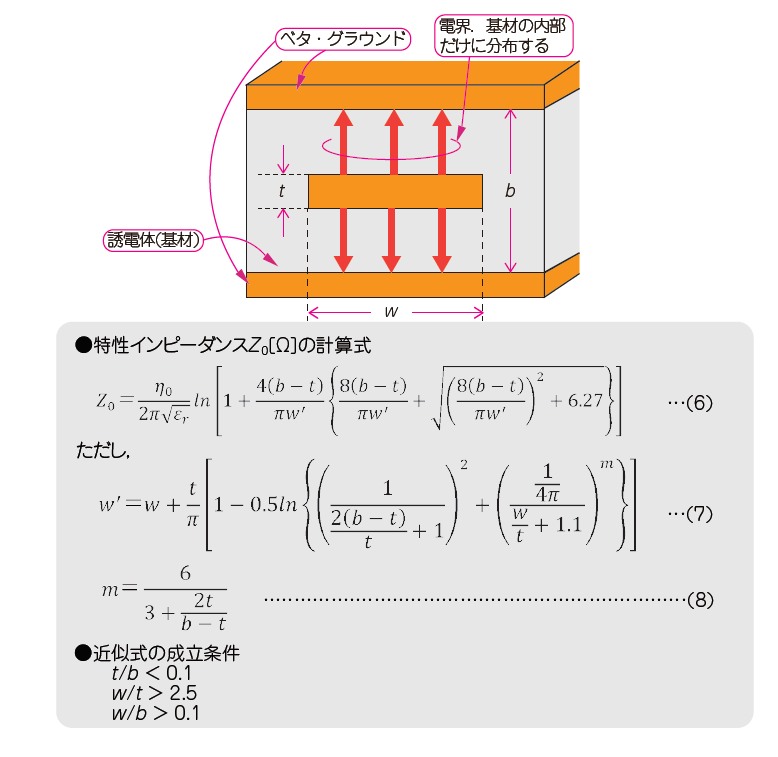
②ストリップ・ラインの近似式

図10の(6)に，多層基板の内側に伝送線路を配し，上下層をグラウンドにした「ストリップ・ライン」の特性インピーダンスを求める近似式を示します．

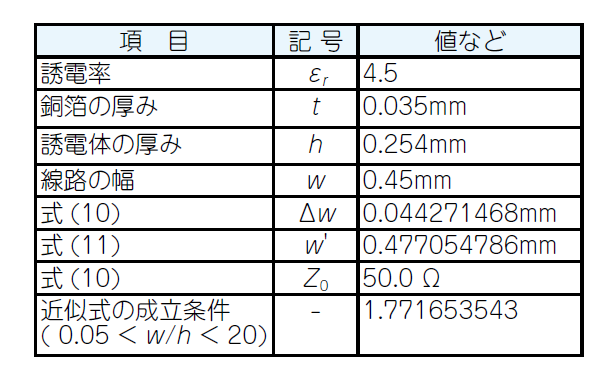
プリント基板の厚さ($b$)が大きかった時代は，線路の導体厚み($t$)と幅($w$)の比が大きかったので，導体厚みを無視して近似式を利用していましたが，最近は，厚さ($b$)が小さくなっているため，$t$と$w$の大きさが近いため無視できません．図11の式は，$t$で$w$を補正しています．

電界がプリント基板内部に閉じ込められるため，ほかの線路に干渉しにくい(クロストークが発生しにくい)構造です．欠点は，伝送線路が表層を通るマイクロストリップ・ライン(後出)より誘電損も銅損もに大きいことです．これは，インピーダンスを確保するために線路が細くなり，また誘電体に囲まれているからです．

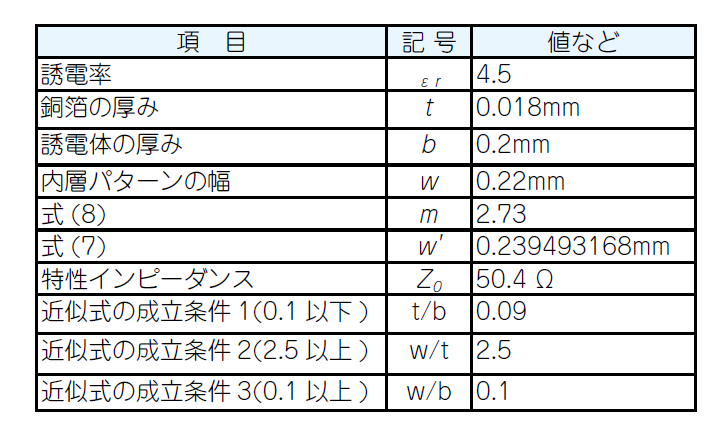
表1に特性インピーダンスの計算例を示します．

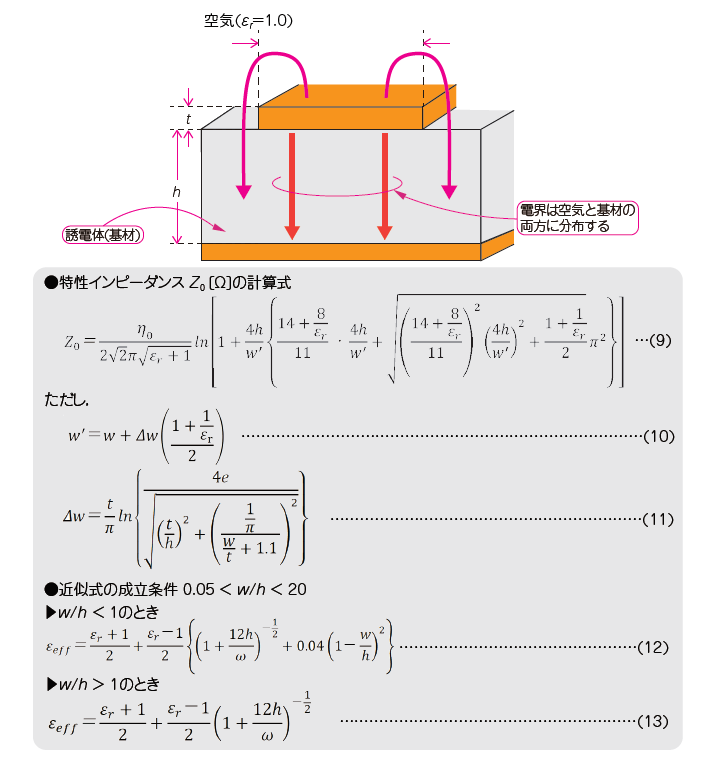
③マイクロストリップ・ラインの近似式

図11の式(10)は，マイクロストリップ・ラインの特性インピーダンスを求める近似式です．表2に計算例を示します．

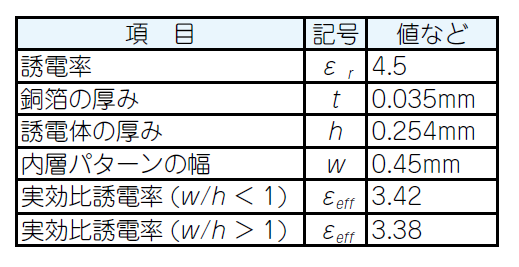
基板の表層に伝送線路を，直下の層にグラウンドを配しています．前出のストリップ・ラインよりも構造が複雑で，空中から誘電体内部にまで広く電界が分布します．その結果，波長短縮率の計算式は複雑です．

式(14)と式(15)は，実効比誘電率$\varepsilon_{eff}$を求める式です．式(5)の$\varepsilon_{r}$を$\varepsilon_{eff}$に置き換えると，波長の短縮率が求まります．実効比誘電率は，線路パラメータによって空気と誘電体の間の値を取ります．表3に計算例を示します．

インピーダンスを確保しようとすると線路幅が太くなり，また空間に接しているためにクロストークが発生しやすいです．一方，線路幅が広く，誘電体に囲まれていないため，銅損と誘電損は小さくできます．

コラム　誰でも超広帯域通信体験！ミリ波アップ・ダウン・コンバータ MZ-mmCon1

ミリ波を使った超広帯域通信実験はとにかくお金がかかる

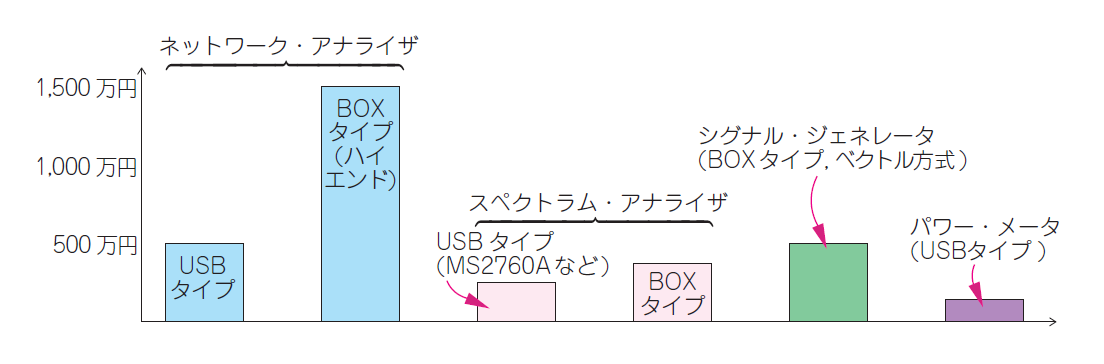
図Aに示すのは，$40 \mathrm{GHz}$まで使えるミリ波システムを開発するときに必要となる市販計測器の価格帯です．

比較的安価なUSBタイプのスペクトラム・アナライザや信号発生器が500万円程度，BOXタイプのネットワーク・アナライザ(ハイエンド機)にいたっては1,500万円もします．USBタイプで揃えても軽く1,000万円を超えます．BOXタイプでそろえると，3,000万円を覚悟しなければなりません．これでは，注目の超広帯域ミリ波5Gの技術に触れたくても手も足もでません．

超広帯域通信を試せるスタータ・キット

写真Aに示すのは，ミリ波帯の通信実験ができるアップ・ダウン・コンバータ(MZ-mmCon1，ミリコン・ワン)です．これ1台で，高価な計測器を使わなくても，ミリ波通信を体験できます．現在，2次試作機を評価中で，2021年1月～3月に発売し，本キットを使った実習セミナを開催する予定です．

S

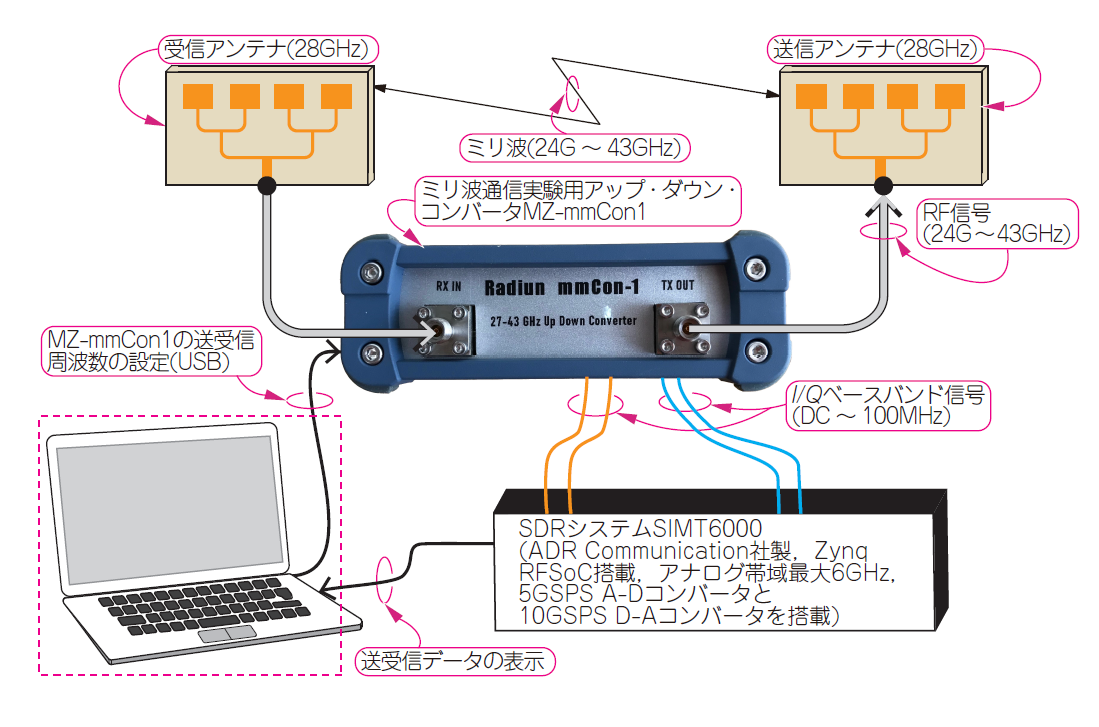
MZ-mmCon1は，帯域$5\mathrm{M}～6\mathrm{GHz}$のベースバンド信号を$27\mathrm{G}～43\mathrm{GHz}$のどこかの帯域($6\mathrm{GHz}$)のRF信号に周波数を上げることができます．また，アンテナから送信したRF信号を別のアンテナで受信して，$5\mathrm{M}～6\mathrm{GHz}$のベースバンド帯域に周波数を下げることができます．

ザイリンクス社のSoC開発用FPGA Zynqを搭載したEclipse Z7(Digilent製，約10万円，写真B)と組み合わせれば，$100\mathrm{MHz}$以上の広帯域通信の実験が可能です．

前述の高額な計測器は，測定値を補償してくれますが，MZ-mmCon1はそこをあきらめて低価格化を目指しています．

MZ-mmCon1でできること

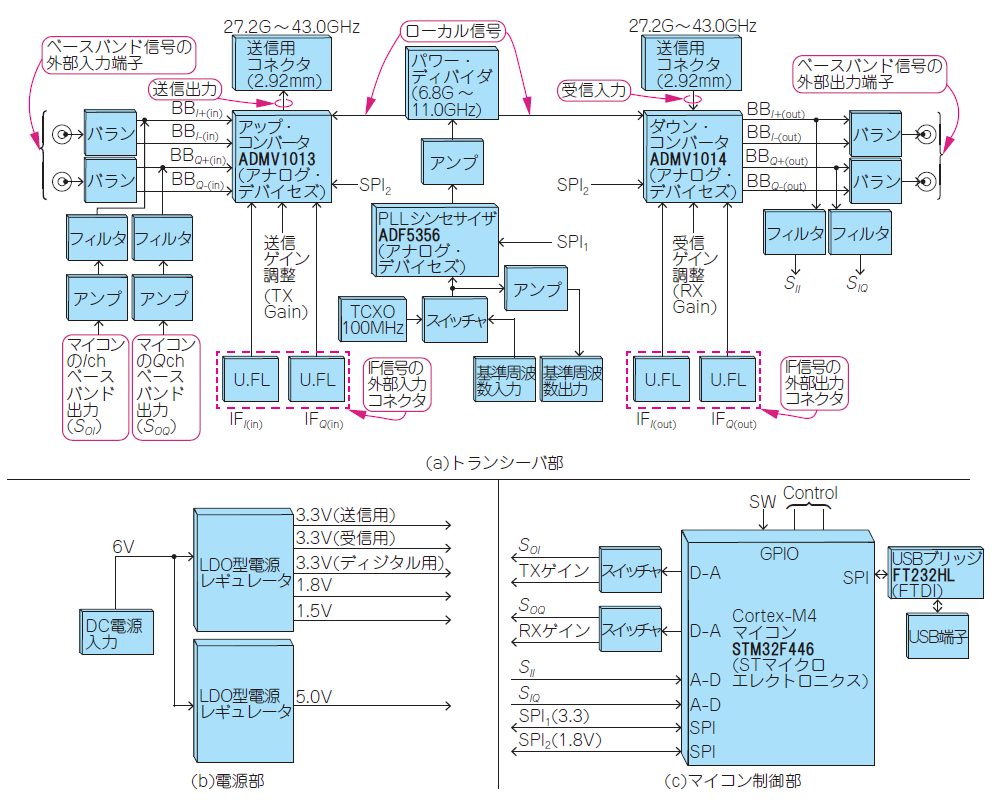
図Bに示すのは，MZ-mmCon1のブロック図です．送信回路と受信回路，そしてそれらを駆動するPLLシンセサイザを搭載しています．

A-DコンバータとD-Aコンバータを内蔵するSTM32マイコンでベースバンド信号を入出力すれば，本機だけでミリ波のデータ通信が可能です．D-Aコンバータで出力したベースバンド信号(最高100kHz)をミリ波周波数にアップして，アンテナからRF信号を送信します．この信号を別のアンテナで受信して周波数ダウンし，A-Dコンバータでベースバンド信号を再生します．

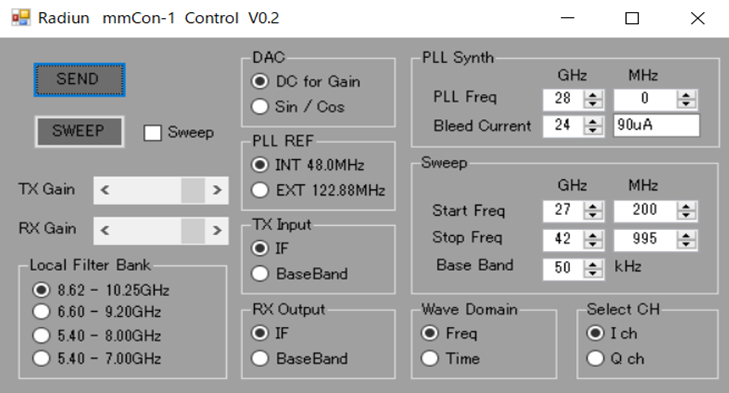
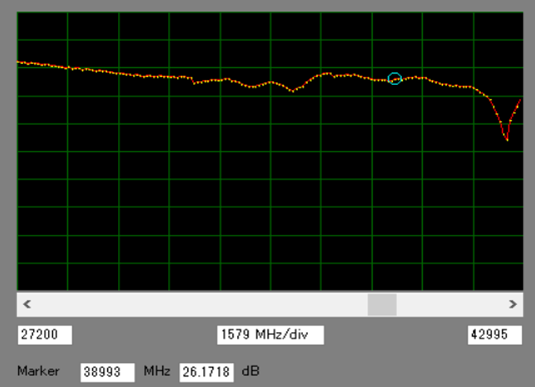
変調周波数やゲイン調整，PLL用フィルタ・バンクの切り替えるときは，専用のWindowsアプリケーションを利用し，USBを介してSTM32マイコンと通信します(図C)．図Dに示すのはMZ-mmCon1の送信出力における周波数特性の平坦度です．STM32マイコンを使ってPLLの出力周波数を$27.2\mathrm{G}～42.995\mathrm{MHz}$の範囲でスイープさせて測ったものです．

図Eに示すのは，MZ-mmCon1の使用例です．高速A-D/D-Aコンバータの数$\mathrm{GSPS}$のベースバンド信号をミリ波に周波数アップしたり，周波数ダウンする部分に利用しています．複数チャネルの高画質動画を送受信する実験も可能です．研究機関でもすでに採用実績があります．

(c) Takashi Kato