5G時代の先進ミリ波ディジタル無線実験室[Vol.3 電磁波の漏れが少ない伝送線路]
次世代高速移動通信と高分解能レーダのキー・テクノロジ
- 著者・講師:株式会社ラジアン(加藤 隆志/Takashi Katou)
- 企画編集・主催: ZEPエンジニアリング株式会社
【Index】
- Vol.1 ミリ波の性質と広帯域通信の実験環境
- Vol.2 反射の起こらない線路を作る
- Vol.3 電磁波の漏れが少ない伝送線路
- Vol.4 信号が減衰しない基板
- Vol.5 高周波センスを磨く!スミス・チャート
- Vol.6 部品や伝送線路の入出力特性モデル「$S$パラメータ」
- Vol.7 高速データ伝送 成功の鍵「群遅延」
- Vol.8 初めての28GHzミリ波伝搬実験
- Vol.9 帯域優先?精度優先?2種類の周波数変換方式
ミリ波通信実験用アップ・ダウン・コンバータ mz-mmCon1を例に,$27\mathrm{G}~40\mathrm{GHz}$の超高周波「ミリ波」を伝送する基板や回路の設計技術を解説します.〈ZEPマガジン〉
今回(Vol.2)は,伝送線路設計の重要な第一歩である,反射の発生しない伝送線路の作り方を説明しました.また,高周波信号や高速ディジタル信号の目でみた,伝送線路の電圧-電流応答「特性インピーダンス」が低周波回路のインピーダンスと何が違うのかも解説しました.また,同軸ケーブル,ストリップ線路,マイクロストリップ線路を例に特性インピーダンスの計算方法も紹介しました.
プリント基板上の伝送線路を高周波電流の流れ方が直流電流とどのように違うのか,そして,高周波電流が流れる伝送線路からどのような電磁界が周辺に放射されるのかも理解します.どのような構造の伝送線路がノイズ放射が少なく,クロストーク干渉が起きにくいのかをそのメカニズムと理由を説明します.
[PR]従来の測定器でミリ波実験!周波数変換アダプタ・キット z-mmcon2
写真Aに示すのは,1台でミリ波を使ったディジタル無線通信が可能な$I/Q$変調&周波数コンバータ“z-mmcon2”(開発:ラジアン)です.ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1の後継機です.
<a “=”” href=”https://www.zep.co.jp/wp-content/uploads/2026/01/p0.png”>

写真A 1台でローカル5Gのミリ波無線通信の実験が可能なアップ・ダウン・コンバータ z-mmcon2(mz-mmcon1のC/Nを大幅に改善した後継機 (開発:株式会社ラジアン)
- 送信周波数範囲:24.0G~44.0GHz
- 送信出力範囲:+10~-29dBm(信号の条件 CW)
- 送信ゲイン範囲:+20~-19dB($I/Q$動作時)
- 受信周波数範囲:24.0G~44.0GHz
- 受信入力範囲-:10dBm以下(信号の条件 CW)
- 受信ゲイン範囲:+12~-9dB($I/Q$動作時)
- 受信雑音指数:10dB以下
- ベースバンド周波数範囲:DC~100kHz(内蔵D-Aコンバータ,外部アクセス不可)
- ベースバンド・レベル範囲:0dBm以下(内蔵D-Aコンバータ,外部アクセス不可)
- IF周波数範囲:1G~6GHz(本体背面のSMA端子)
- IFレベル範囲:0dBm以下(本体背面のSMA端子)
- 電源:付属のACアダプタ(DC6V,2A)
- 消費電流:1.5A(通常動作時)
- 基板サイズ:128×93×1.6mm(基材はRogers4350B)
- ケース・サイズ:$W$=140mm $D$=129mm $H$=40mm(フランジ含む)
1.伝送線路の電流と電界に注目!
RF電流とDC電流がとるルートは違う
電流は,往路と復路が揃って初めて流れます.つまり,電流が流れると必ずループが形成されます.
電流がループを形成するのは,DC(直流)でもRF(Radio Frequency,高周波)でも同じです.しかし厳密に見ると,流れるルートは,RF電流とDC電流で異なる場合が多々あります.
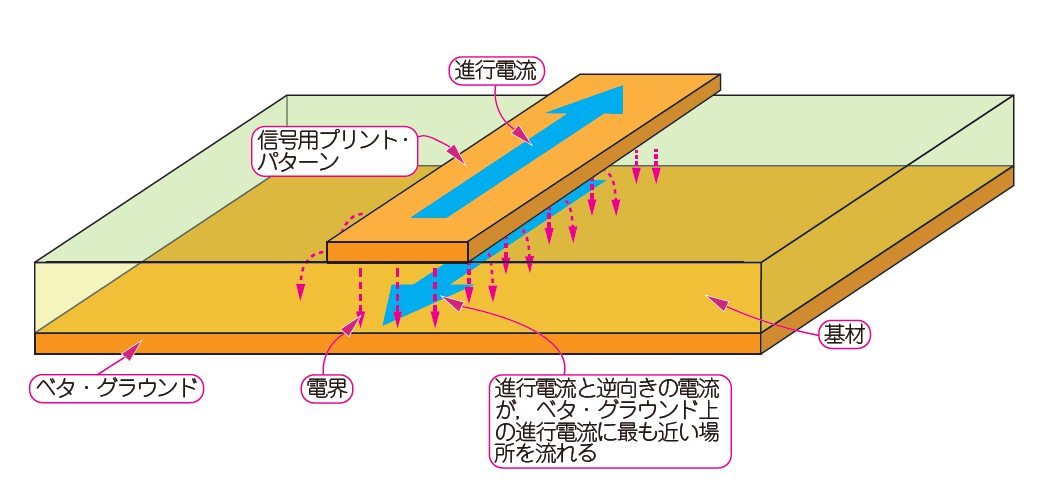
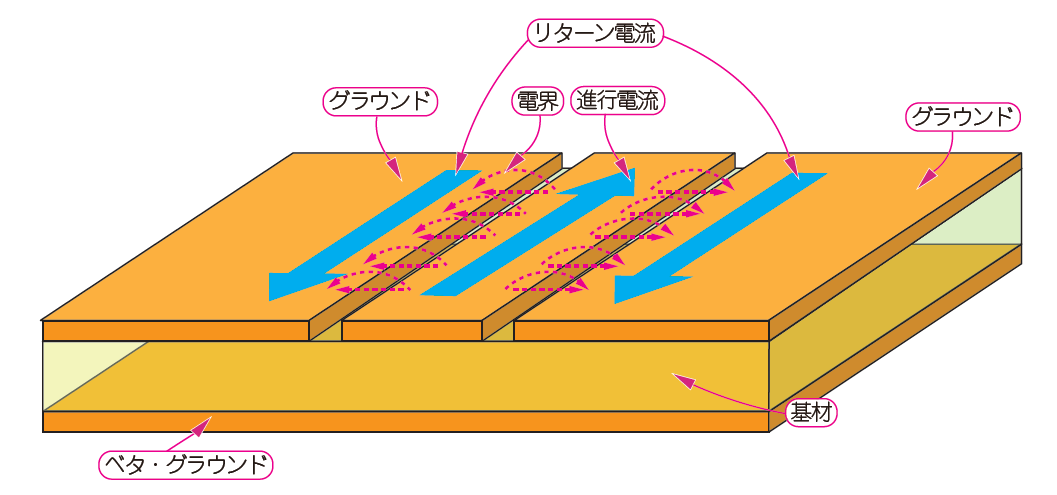
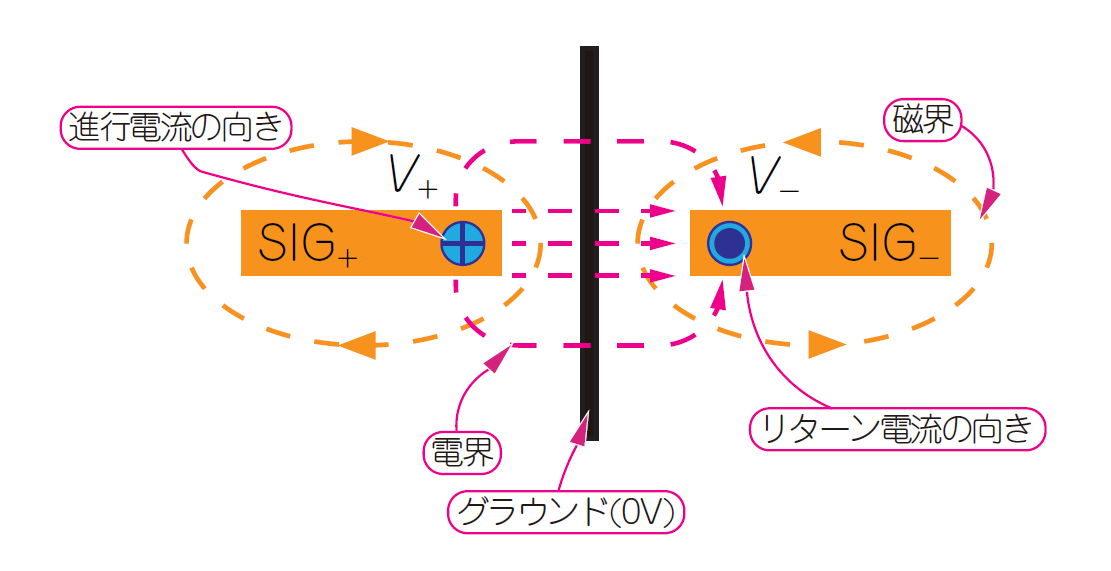
図1に示すのは,Vol.2で紹介した高周波信号の代表的な伝送線路「マイクロストリップ線路」です.電流の往路は「進行電流」,復路は「リターン電流」と表しました.
図1 電流は必ず行って帰ってくる直流電流のリターン電流が戻るときは,一番抵抗値の低いところを選ぶ.高周波電流は,進行電流の一番近い場所を選んで流れる.図のマイクロストリップ線路の場合,リターン電流は伝送路の直下を流れる.高周波電流が流れるプリント・パターンを見るときは,このような目で観察する
RF電流は交流ですから,実際には進行電流とリターン電流の向きは瞬間的に入れ替わります.ここでは便宜上,一方向に固定して表現しました.ある瞬間の電流の向きと考えてください.
前述のとおり,RF電流は表層の伝送路を進行し,ベタ・グラウンドを通って戻ってきます.DCのリターン電流は,ベタ・グラウンドの最も抵抗値の低い箇所を選んで通り,そこの電流密度が最大になりますが,RF電流は,進行経路に一番近い箇所を選んで流れます.空間には進行電流とリターン電流を電界が結ぶように分布します.
高周波のプリント・パターンを描くとき,このリターン電流のイメージがあるかないかで,仕上がりの性能に大きな差が出ます.
「電界」と「電流」を一緒にイメージする
図2に示すのは,図1に示すプリント基板の断面です.電流の向きは,手前から奥へを“+”で,奥から手前へを“●”で表しました.
電界は,金属の端などの尖った部分に集中する性質があります.RF電流も電界と同様に尖った部分に集まって流れます.図2に示す伝送路を流れる進行電流は,プリント・パターンの端の狭い範囲に集中します.
一方,ベタ・グラウンドは面状になっているため,電界が緩やかに分布します.そのため,進行電流の直下の一定の範囲に広がります.基材(誘電体)が薄ければ,電界は狭い範囲に収まるため,リターン電流も狭い範囲を流れます.
以上のように,プリント基板の形状によって電流の分布は異なりますが,進行電流とリターン電流は狭い範囲でペアになっています.
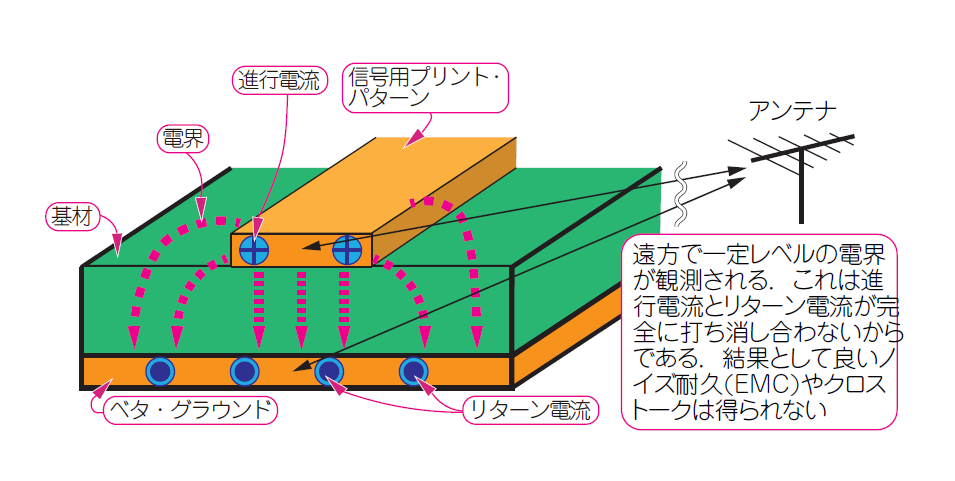
図2 図1のマイクロストリップ線路は電界が放射されるベタ・グラウンドを流れるリターン電流は進行電流よりも広い範囲を流れる.その結果,進行電流とリターン電流の間に電界を封じ込めることができず,広範囲に分布する.クロストークの発生やノイズ放射が起こりやすい構造である.遠方とは,プリント・パターンの幅や基板の厚みに対して十分(10倍以上)な距離のこと.例えば$W=1.0\mathrm{mm}$,$H=1.0\mathrm{mm}$なら,$10\mathrm{mm}$以上
2.電磁界を漏らさない①「差動線路」
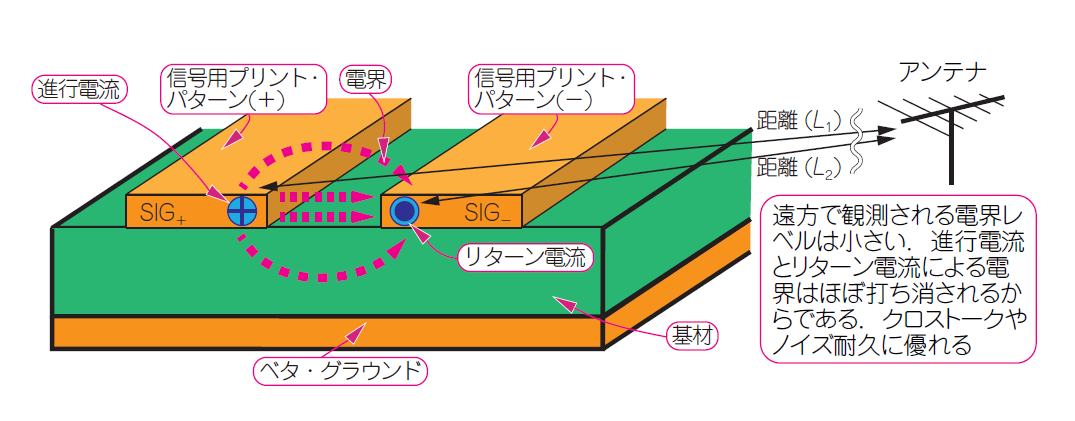
マイクロストリップ線路は電磁界が漏れる
図2に示したマイクロストリップ線路を流れるRF電流は,プリント・パターンの表層部を流れるため,電界の放射が大きく,クロストークも発生しやすいです.
プリント基板の遠方の電界を観測すると,進行電流分布の中心と観測点の距離($L_1$)と,リターン電流分布の中心と観測点の距離($L_2$)が等しく,進行電流とリターン電流の合計がゼロになる(または等しい)場合は,観測点で電界は打ち消されてゼロになるはずです.ここでいう遠方にある観測点は,$10×10~30×30\mathrm{cm}^2$ のプリント基板上の点をイメージしています.プリント・パターン間や基板の厚みなどの形状の違いによる影響が無視できるほど十分な(10倍以上)距離があるという意味です.
ところがマイクロストリップ線路は,進行電流とリターン電流の分布が異なりますから,観測点での電界はゼロになりません.観測点が近いほど電界レベルは高くなります.特に,信号用プリント・パターンに隣接して平行に走る伝送路には,強い電界が加わり,影響を及ぼします.この現象を「クロストーク」と呼びます.配線どうしの距離が近いほど,$L_1$と$L_2$の差は大きくなり,お互いに強い電界を加え合うことになります.マイクロストリップ線路は,近接信号の影響を受けやすく,与えやすい伝送線路です.
なお,ここでは電界だけを考えました.これは空間での磁界が電界と比例関係(比例定数は空間インピーダンス$120\pi\Omega$)だからです.
専用のリターン線路とペアにして相殺する
ノイズに強くクロストークが発生しにくい「差動線路」
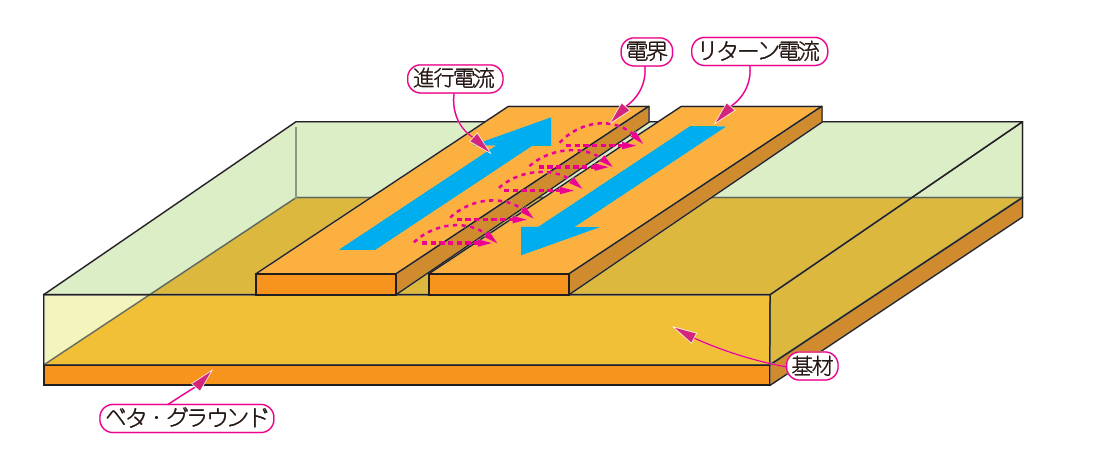
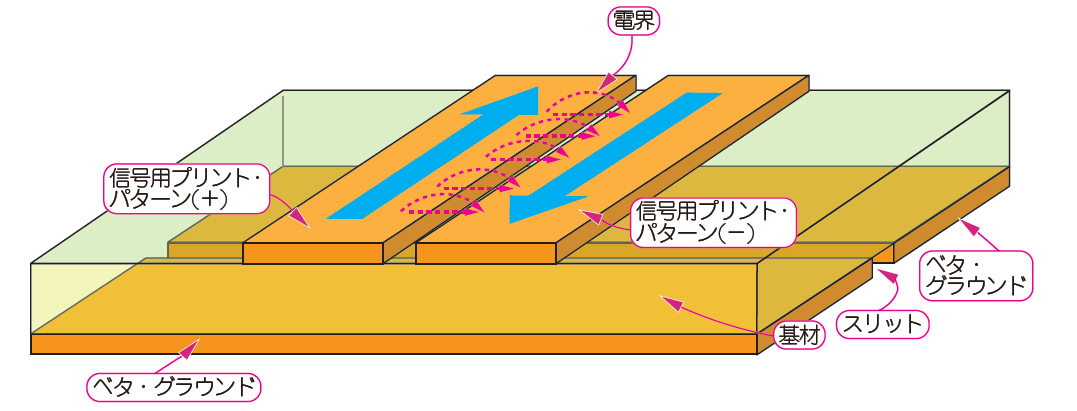
図3に示すのは,マイクロストリップ線路の弱点である「クロストーク」の発生が少ない「差動伝送路」です.
差動伝送路は,進行電流用の線路と同じ信号層にリターン電流専用の線路を追加して,進行電流用の線路に寄り沿わせた構造をしています.この伝送線路なら,リターン電流がベタ・グラウンドに流れなくなります.
図3 専用のリターン電流用の線路を進行電流のすぐ隣に寄り添わせた「差動線路」平行する2本の線路間にほとんどの電流と電界が集中するため,ベタ・グラウンドにはほとんど電流が流れない
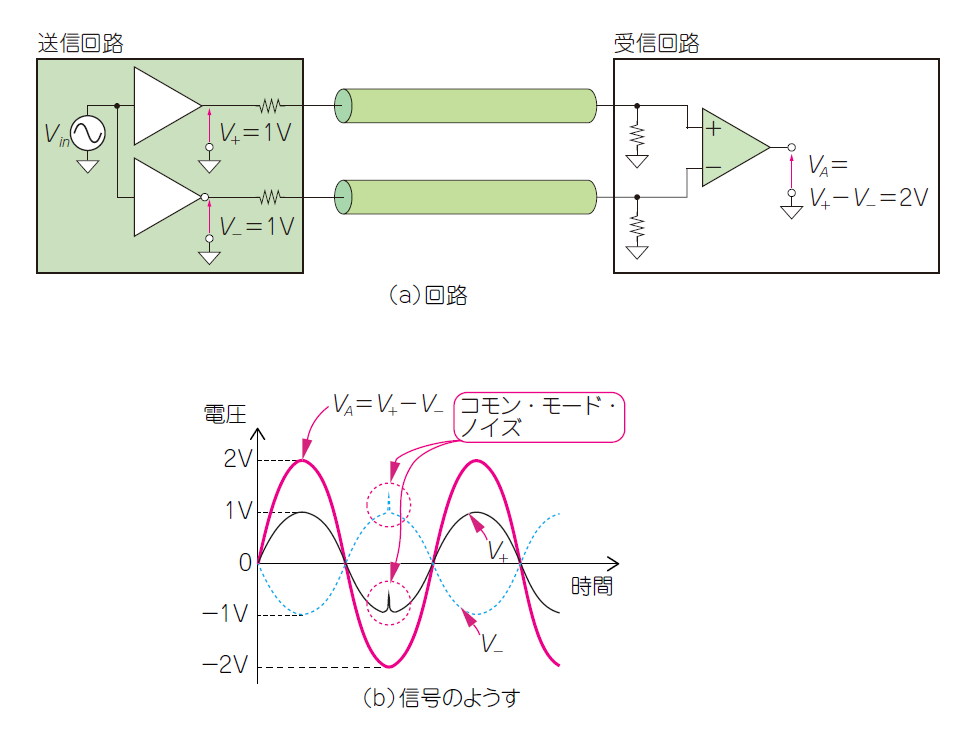
専用のドライブ回路
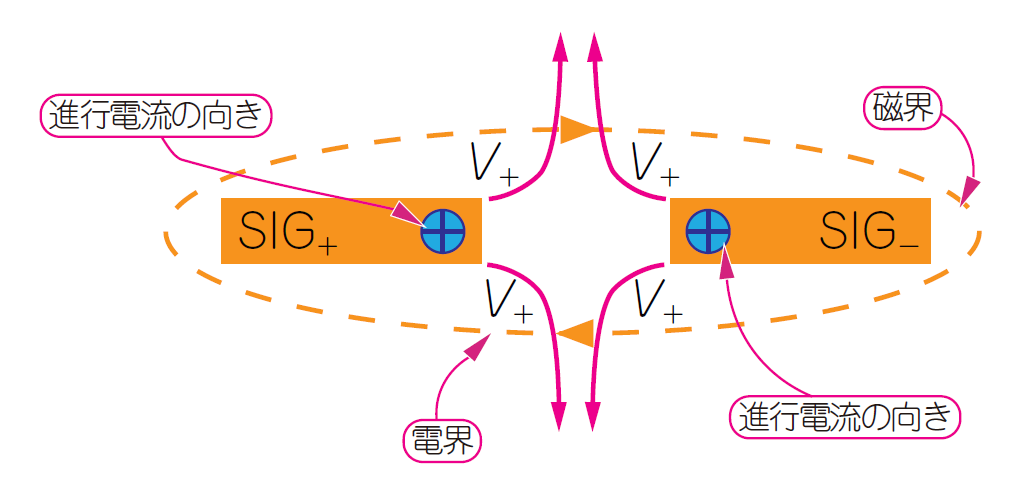
図4に示すように,差動伝送路は,1つの信号源の出力信号を極性が互いに$180^{\circ}$違う2つの信号($V_+$信号と$V_-$信号)に換えて駆動します.受信回路には2つのポートがあり,送信回路から差動伝送路を伝わってきた$V_+$信号と$V_-$信号を受けて,差分($V_+-V_-$)を取り出します.
図4 差動伝送路は極性が$180^{\circ}$違う2つの信号で駆動し,その差分を受信回路で取り出す信号の振幅が2倍になるだけでなく,ノイズを浴びても受信回路で除去される.ノイズの影響を受けにくく,かつノイズを放射しない優れた伝送線路である
$V_+=V-=1\mathrm{V}_{\mathrm{peak}}$とすると,伝送される信号の振幅がその差分の$2 \mathrm{V_{peak}}$になります.$V_+$信号と$V_-$信号の両方に同時に重畳するノイズは,受信回路の引き算によって打ち消される効果も得られます.
差動伝送路の電界の分布
図5に示すのは,差動伝送路の断面です.
進行電流とリターン電流は互いに最短距離を流れるため,電界と電流は,線路間のスリットの極めて狭い場所に集中し,その結果,遠方で電界を観測すると,ほとんどゼロになります.
以上のような理由で,差動伝送路は,クロストークやノイズ放射や耐性に優れています.
図5 差動線路は電流と電界が狭い範囲に集中するその結果,周辺の影響を受け難くまた影響も与えにくい.差動線路は,ギルバート・セルを使った差動タイプのRFアナログICどうしを接続するときによく利用される
プリント・パターンを自由に描ける
部品の実装密度が上がってくると,たとえプリント基板の層数を増やしても,面積の大きなベタ・グラウンドを確保することは難しくなります.
こうなると,伝送路のリターン電流が流れる経路が進行電流が流れるプリント・パターンと離れ離れになります(図6).リターン電流はどんな状況下だろうとも,進行電流との距離が最短になるルートを確実に選んで流れます.リターン電流の経路が絶たれていても,リターン電流はベタ・グラウンド間の容量や浮遊容量,パスコンなど,すべての選択肢の中から最短ルートを選んで元(信号源)に戻ってきます.
このように実装上の事情から,リターン電流が迷走するようなプリント・パターンを描くと,伝送路の特性インピーダンスが大きく乱れて,反射や信号の減衰,定在波が発生します.定在波が発生すると,伝送線路にエネルギが蓄積されて,電流が増します.結果として大きなノイズが放射されます.
図6 ベタ・グラウンドの切れ目によってリターン電路を絶たれた電流は迷走して浮遊容量やパスコンなどを流れる実装密度の高い基板では,進行電流の下層のすべてを連続したベタ・グラウンドで埋め尽くすことができない場合がある.特性インピーダンスが乱れて定在波が発生し大きなノイズが放射される原因になる
差動伝送路は,この課題にも対処できます.図7に示すように,リターン電流の専用経路が確保されているため,信号用プリント・パターンの下層にあるベタ・グラウンドにスリットによってリターン電流の経路が絶たれようが支障はありません.
図7 差動線路はリターン電流専用の伝送線路があるため,図6のリターン電流の経路が絶たれるような問題は発生しない
差動伝送路の課題
$\mathrm{GHz}$以上の超高周波では$180^{\circ}$の位相差合わせが難しい
以上のように差動伝送路は,高周波特性の優れた線路ですが,信号の周波数が$\mathrm{GHz}$を超えると扱いが難しくなります.
図4で説明したように,極性の違う2つの信号の位相が正確に180°ずれるように厳密なコントロールが必要です.この制御は周波数が高くなるほど難しくなってきます.わずかな遅延が大きな位相のずれにつながります.特に難しいのは,伝送線路の曲がり部分です.内側と外側の半径差による線路長のわずかな差が問題になったりします.
GHz以上での特性インピーダンスの制御が難しい
2本の線路間を流れる信号の位相関係(結合モード)によって,特性インピーダンスが変わり,計算式も違います.結合モードが差動のときを「奇モード」と呼び,同相のときを「遇モード」と呼びます.
差動信号の位相差がピッタリ$180^{\circ}$ならば,計算式どおりの特性インピーダンスを実現でき,反射などの問題に見舞われることはありません.ところが,周波数が$\mathrm{GHz}$を超え,差動間でわずかに位相がずれてくると,実際の特性インピーダンスが計算とずれてきて,反射が大きくなりロスや定在波が発生します.このような伝送線路に高速のディジタル信号を通すと波形が崩れます.
FR-4などのプリント基板は,ガラス繊維を編んでできた基材を使っており,場所によって誘電率などの均一性がありません.どんなに注意深く差動線路を設計しても,2本の信号に数$\mathrm{ps}$~数十$\mathrm{ps}$の遅延差が生じます.設計要件によりますが,この遅延差で許容できる上限はせいぜい$10\mathrm{GHz}$以下でしょう.ミリ波基板では,エッチングによる高精度な薄膜パターンを形成できるアルミナを使うことがあります.
特性インピーダンスの算出に使う近似式
差動伝送路の特性インピーダンスを求める式は,近似式でも複雑です.
また,差動線路は,その形状を1つに代表させることが困難です.例えば,2本の線路の位置関係が上下になっていたり,線路の両脇にグラウンドがあったりなかったり,シールドが付いていたり(USBなど),その形態はいろいろです.教科書を見ても,差動線路だけは特性インピーダンスを求める式がたくさん掲載されています.
図8に示すのは,ストリップ型の差動線路です.
次に示すのは,特性インピーダンス$Z_{\mathrm{diff}}$を求める近似式です.ここで,$\eta_0$は真空中の特性インピーダンス,$\mu_0$は真空中の透磁率,$\varepsilon_0$は真空中の誘電率です.また,図8(b)は計算例です.
\begin{equation}
Z_0=\frac{\eta_0} {2\pi \sqrt{\varepsilon_r}}
\ln{
\left[
1 + \frac{4(b-t)} {\pi w^{\prime}}
\left(
\frac{8(b-t)} {\pi w^{\prime}}
+
\sqrt{\left( \frac{8(b-t)} {\pi w^{\prime}} \right) ^2 + 6.27}
\right)
\right]
}
\end{equation}
\begin{equation}
w’ = w +
\frac{t}{\pi}
\left[
1 – 0.5 \ln\left(
\left(
\frac{1}{\frac{2(b-t)}{t} + 1}
\right)^2
+
\left(
\frac{\frac{1}{4\pi}}{\frac{w}{t} + 1.1}
\right)^m
\right)
\right]
\end{equation}
\begin{equation}
m=\frac{6} {3+\frac{2t}{b-t}}
\end{equation}
\begin{equation}
\eta_0=\sqrt{\frac{\mu_0}{\varepsilon_0}}
=120\pi\approx377
\end{equation}
\begin{equation}
Z_{\mathrm{diff}}=2 \times Z_0
\left[
1-0.347e^{-2.9\frac{S}{H}}
\right]
\end{equation}
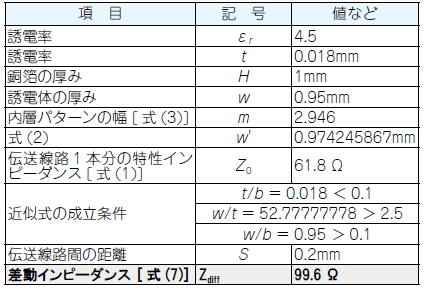
(b)特性インピーダンスの計算例図8 最もよく使われている内層配線型のストリップ差動線路と特性インピーダンスの計算例
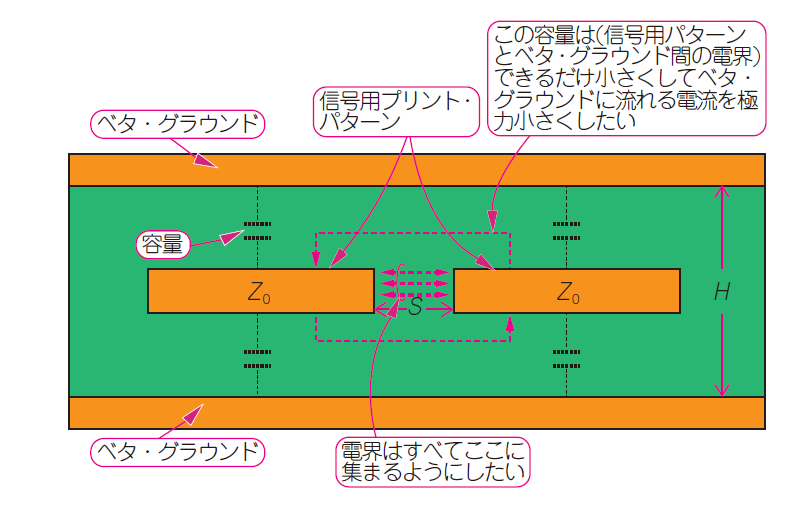
最初に,式(3)を使って1本の伝送線路の特性インピーダンス($Z_0$)を求め,次に2本の線路間距離($S$)から差動の特性インピーダンス($Z_{\mathrm{diff}}$)を算出します.伝送線路に発生する電界は,1本のときより2本のときのほうが大きくなるため,容量が増えて特性インピーダンスが下振れします.
$50\Omega$線路を差動にすると,特性インピーダンスは$100\Omega$になります.しかし,2本の伝送線路間の間隙($S$)が小さくしていくと,結合が強まって$100\Omega$よりずっと低い値になります.そこで実際に設計するときは,結合の強さを想定してあらかじめ,1本のときの特性インピーダンス($Z_0$)を大きくしておきます.
誘電体の厚み($H$)を2本の線路の間隙($S$)より大きくするほど,ベタ・グラウンドにまったく電流が流れない純粋な差動伝送路に近づきます.
なお,図8の差動線路は前回紹介した「ストリップ線路」になっています.この線路は,すべての電界が誘電体内にあり,信号の波形は$1/\sqrt{\varepsilon_r}$に短縮されるので,その分の遅延を考慮する必要があります.
3.ミリ波では「コプレーナ線路」を多用する
ビアに信号を流さない
プリント基板の表層にあるICやコネクタを内層のベタ・グラウンドと接続するときは,必ずビアを使って接続します.このビアは,高周波でインダクタンス性を示します.精密に配置を調整したり,特性インピーダンスを$50\Omega$にピッタリ合わせたりしても,ミリ波のように$30\mathrm{GHz}$を超えるとインダクタとして機能するため,リターン電流が流れにくくなります.
この問題を解決できるのが,図9に示す伝送路の近傍をベタ・グラウンドで挟む「コプレーナ線路」です.グラウンドがプリント基板の表層にあるので,ビアの影響を小さくできます.内層グラウンドにもリターン電流を流す構造のものや,内層グラウンドは設けない構造のものがあります.
コプレーナ線路は,非平衡線路なのに平衡線路に近いシンプルな伝送路を作れます.コンパクトに配線すれば,$100\mathrm{GHz}$まで通すことも可能です.ミリ波クラスの極めて周波数の高い信号を扱うデバイスは,すべて非平衡伝送タイプですから,コプレーナ線路を使う場合が多くなります.
ベタ・グラインドのないコプレーナ線路では,容量は表層にしかできません.つまりすべての電界は表層の信号パターンとグラウンドの間に分布します.
図9 30GHzを超えるミリ波を通すときに利用するコプレーナ線路進行電流の伝送路の両サイドをリターン電流用のグラウンド・プレーンで挟む.差動線路と同様に進行電流もリターン電流も表層に多くのリターン電流を流す.内層グラウンドをリターン経路に利用する伝送線路は,グラウンドとの接続に使うビアがインダクタとしてふるまうため,高周波電流が流れにくくなるが,この構造なら,表層で実装することの多いICもビアを使わずにのグラウンドを処理できる.コネクタの信号の接続も容易である
特性インピーダンスの算出に使う近似式
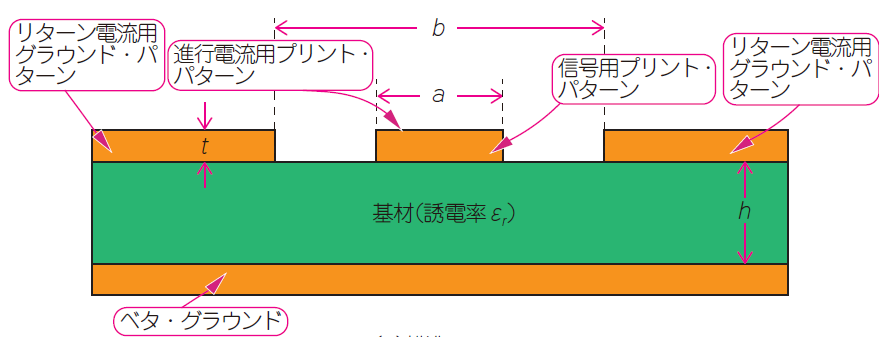
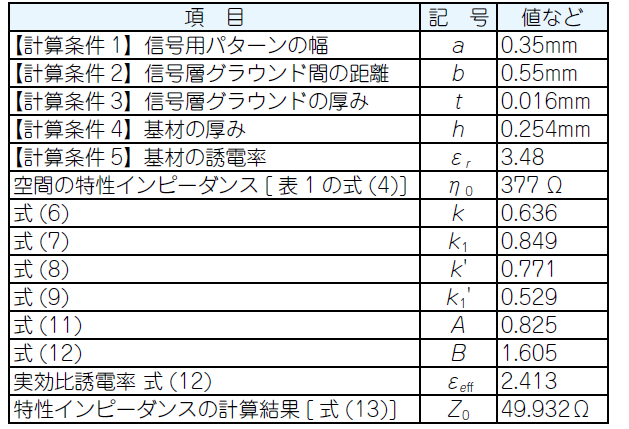
図10に示すのは,コプレーナ線路の断面です.電界は誘電体中と空中に分布します.以下に,特性インピーダンスの計算式を示します.
\begin{equation}
k=\frac{a}{b}
\end{equation}
\begin{equation}
k_1=\frac{
\tanh{
\left(
\frac{\pi a}{4h}
\right)
}
}
{
\tanh{
\left(
\frac{\pi b}{4h}
\right)
}
}
\end{equation}
\begin{equation}
k^{\prime}=\sqrt{1-k^2}
\end{equation}
\begin{equation}
k_1^{\prime}=\sqrt{1-k_1^2}
\end{equation}
\begin{equation}
A=\frac{k}{k^{\prime}}
\end{equation}
\begin{equation}
B=\frac{k_1}{k_1^{\prime}}
\end{equation}
\begin{equation}
\varepsilon_{eff}=\frac{1+\varepsilon_r AB}{1+AB}
\end{equation}
\begin{equation}
Z_0=\left(
\frac{\eta_0}
{2\sqrt{\varepsilon_{eff}}
}
\right)
\frac{1}{A+B}
\end{equation}
図10(b)に特性インピーダンス($Z_0$)の計算例を示します.コプレーナ線路は,たいてい多層のプリント基板で利用されるため,内層にベタ・グラウンドがある状況で使える近似式です.進行電流用パターンをはさむ2つのリターン電流用グラウンド間の距離($b$)を層間厚み($h$)よりも小さくするほど,表層の信号パターンと両サイドのグラウンド・パターンの間にすべての電界が分布する,純粋なコプレーナ線路に近づきます.
図10 コプレーナ線路の特性インピーダンスの計算式
4.有限要素法 電磁界シミュレータのしくみ
マクスウェルの方程式を解かせている
かつて高周波回路の設計は,ベテラン技術者の勘と経験によって行われていました.奥義の会得には多くの年月が必要と言われていました.
高周波回路も電磁界も,所詮は物理学の世界ですから,計算できないはずがありません.そして90年代初頭,「マクスウェルの方程式」に基づいて電磁界のふるまいをコンピュータで計算するシミュレータが広く普及し始めました.現在では,空間に分布する電磁界を厳密に計算する3次元対応のものから,プリント基板のように平面に特化して高速化した2.5次元対応のものまで,さまざまな製品が市販されています.
電磁界の発生元である金属を微小なアンテナの集合体に置き換える
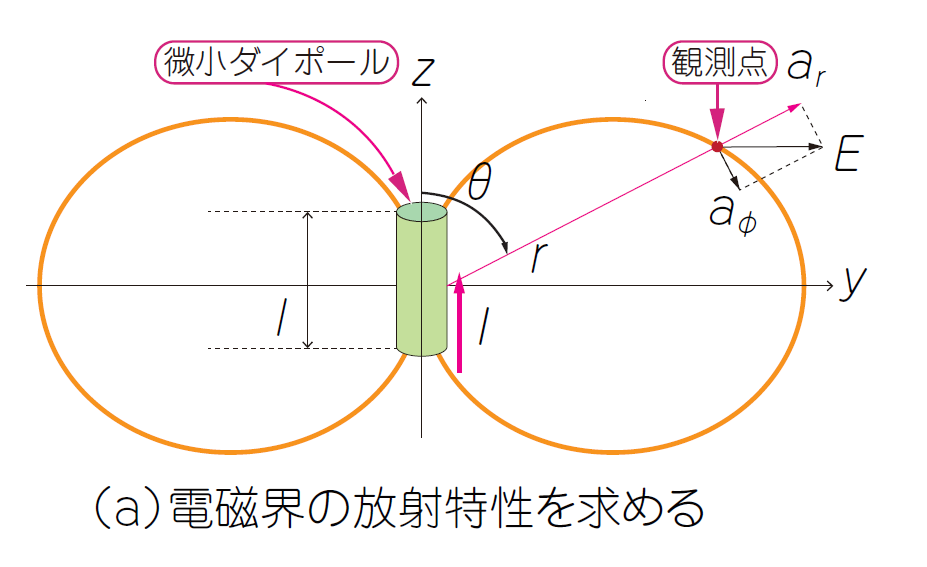
図Aに示すように,配線が放射する電磁界を計算するときは,配線を微小なダイポール・アンテナでモデリングします.
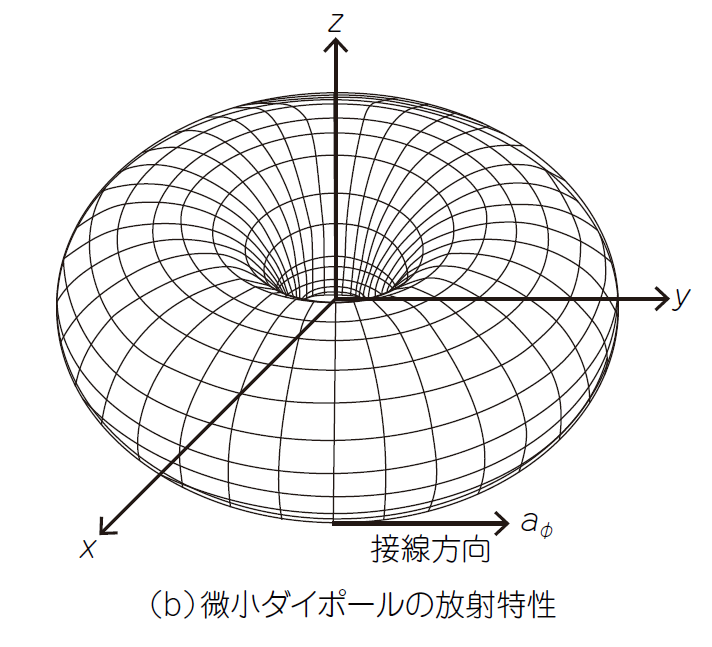 |
|---|
| 図A 電磁界シミュレータ(有限要素法タイプ)は伝送線路を微小なダイポール・アンテナが集まったものと見なして電磁界分布を計算する |
微小ダイポール・アンテナとは,波長よりも十分に短い線路です.微小なダイポール・アンテナとして働きます.微小ダイポール・アンテナを多数集めて解析する手法を「モーメント法」と呼び,メジャーな電磁界解析法のひとつになっています.
微小な長さ$l$の線路に,RF電流($I$)を流したときに,微小ダイポール・アンテナからの距離r,角度$\theta$,$\phi$の点での電界$E$と磁界$H$は,次のように求まります.これらは,マクスウェルの方程式から導き出されるものです.
\begin{align}
E &= -\frac{j\xi Il}{2\pi k}
\left( \frac{jk}{r^2}+\frac{1}{r^3}\right)
e^{-jkr} a_r\cos\theta \nonumber\\
&\quad +\frac{j\xi Il}{4\pi k}
\left( \frac{k^2}{r}-\frac{jk}{r^2}-\frac{1}{r^3}\right)
e^{-jkr}a_\theta\sin\theta \\
H &= \frac{1}{4\pi}
\left( \frac{jk}{r} + \frac{1}{r^2} \right)
e^{-jkr} a_\phi \sin \theta
\end{align}
ただし,$E$:観測点の電界,$H$:観測点の磁界,$I$:微小ダイポール・アンテナに流れる電流,$l$:微小ダイポール・アンテナの長さ,$r$:微小ダイポール・アンテ ナから観測点までの距離,$\theta$:微小ダイポール・アンテナと観測点を結ぶベクトルの$z$軸に対する角度,$a_\phi$:磁界の単位ベクトル,$a_r$:$r$方向の電界の単位ベクトル,$a_\theta$:$\theta$方向の電界の単位ベクトル,$c$:光速,$\lambda$:波長($=c/f$),$\xi$:波動インピーダンス($=120\pi$),$k$:定数($=2\pi/\lambda$)とします.
前述のように,モーメント法では伝送線路を微小ダイポール・アンテナが無数に集まったものと見なします.微小ダイポール・アンテナから一定の距離にある点で観測される電界の分布は,これらのセグメントのすべてから放射された電界を積分すると求まります.
空間や基板上の任意の位置での電磁界分布は,プリント基板上を流れるRF電流と線路の形状がわかれば求まります.さらに「電界の方向は金属表面に対して必ず垂直になる」などの既知の条件を合わせて利用すれば,プリント・パターンの形状と信号源の電圧から基板上のすべての電流密度を求めることができます.
式(14)と式(15)は,電磁界($E$と$H$)は,プリント基板上のRF電流の向きと大きさだけで計算できると言っています.つまり,RF電流の向きと大きさを決める作業,すなわちプリント基板の設計いかんによって,ディジタル信号の伝送波形品質に加え,EMC(Electro-Magnetic Compatibility),クロストーク,放射ノイズなど,製品の生命線である「品質」を決めている,とも言っているのです.コンピュータの進化と優れたシミュレータの誕生によって,高周波回路設計は勘に頼るのではなく,パソコンで正確に予測できる,と技術者は気づかされました.
微小ダイポール・アンテナからの距離と電界レベルの関係
図Bに示すのは,コラムA 式(14)の距離($r$)を変えたときの電界レベルの変化です.波長$1\lambda$のときの電界を0dBとして計算しました.
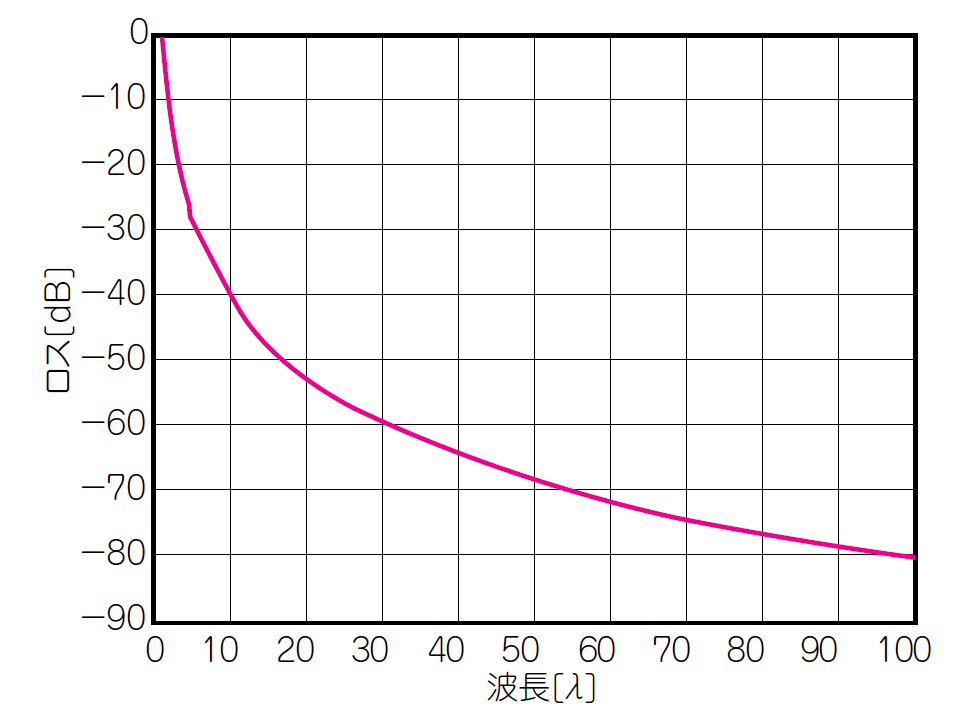 |
|---|
| 図B 電磁波の発生源からの距離($r$)と強さ(ロス) |
| コラムAの式(14)の$\theta=0$としてプロットした結果.近傍では2乗($1/r^2$)や3乗($1/r^3$)で急減衰するが,遠方では$1/r$でゆっくり減衰する.電波が意外と遠くに飛ぶように感じる理由はここにある |
近傍では,コラムAの式(14)の$1/r^2$と$1/r^3$の項が効くため,線路に近づくほど急激に電界が増します.このことから,電流は電磁界に比例しますから,進行電流の近くにリターン電流が集まってくる現象が起きる説明が付きます.つまり,「進行電流が流れる」→「その付近のグラウンド上に電界が発生する」→「グラウンド上の電界の強いところに電流が流れる」→「進行電流とリターン電流の経路が形成される」というロジックです.
遠方では($r$が大きいとき),$1/r^2$や$1/r^3$の項はほぼゼロになり,$1/r$の項だけが残ります.電磁波が思いのほか遠くまで届く理由は,$1/r$で減衰するからです.電波は空間に分散されていきますが,なんとなく2次元(面)で広がっていくため2乗で減衰しそうですが,実際には電磁波は円板状に広がっていて,その円周が増しているだけなので,1次関数$1/r$)で減衰するのでしょう.
5.高周波信号用伝送線路の適材適所
ベテランの間でも意見が分かれる
マイクロストリップ線路,ストリップ線路,差動線路,コプレーナ線路など,高周波信号の伝送線路にはさまざまなものがあります.
周波数や引き回す配線の長さ,使うデバイスの入出力仕様(差動かシングルエンドか),クロストークを減らしたいのか,減衰を抑えたいのか,ディジタル信号なのかアナログ信号なのかなど,さまざまな条件によって最適な線路は違います.非常にパラメータが多いため,最適な線路を選ぶためには,多くの経験で養われるセンスが重要になる場面が少なくありません.ベテランの間でも意見が分かれます.
ここでは,ミリ波5G対応アップ・ダウン・コンバータ MZ-mmCon1(写真A,ラジアン)を例に,どのような視点で伝送線路を使い分けたのかを紹介します.
差動線路の使いどころ
差動線路は,次のようなメリットがあります.
- ノイズに強い
- 放射が小さい
- クロストークが発生しにくい
- ベタ・グラウンドの連続性を維持しなくていい(電気的に異なるベタ・パターンをまたいでもOK)
一方で,配線を引き延ばすと,ペア線を流れる信号の位相差が$180^{\circ}$(逆位相)からずれて特性インピーダンスが変化し,反射や減衰,クロストークが発生します.つまり,差動線路として機能しなくなります.
正しく機能している状態
図Cに示すのは,差動線路の正常な動作状態です.
互いに結合したペア線路の位相が逆になっている状態を「奇モード励振」と言います.正負が逆で,かつ強さが等しいので,ペア線路の中間面の電圧は$0\mathrm{V}$です.つまり,仮想的なグラウンドと見なすことができます.
この仮想グラウンド面をグラウンドと考えて設計した,特性インピーダンスが$50\Omega$のシングルのストリップ線路は,$100\Omega$の差動線路として機能します.
図C 差動線路が正しく機能している状態(奇モード励振)互いに結合したペア線路の位相が逆になっている
機能していない状態
ペア線を伝送する信号の位相がずれてくるとどうなるでしょうか.ペア線を伝送する信号の位相がそろった極端な例で説明します.この状態を「遇モード励振」と言います(図D).
両線路の電圧は極性も強さも等しいため,電界は結ばれません.ペア線の中間にあった仮想グラウンドは消滅して遠方界がグラウンドになります.つまり,容量が減って特性インピーダンスは,図Cよりも大きくなります.
このように差動信号間の位相がずれると,電界や磁界の分布状況とともに特性インピーダンスが変化します.干渉に強いという差動線路の特徴も失われます.
図D 差動線路が機能していない状態(遇モード励振)ペア線を伝送する信号の位相が逆になっていない.図は位相がそろっている極端な例
位相がずれる理由
差動線路の位相がずれる理由は,線路の曲がりや基板の物理的な不均一性です.この位相のずれを「スキュー」(skew)と言います.スキューは,$10\mathrm{cm}$ほど配線を引き回すと数$\mathrm{ps}$以上発生し,線路が長くなるほど増します.
許容できるキューは,使用する帯域や伝送速度によります.アナログ・ベースバンド信号($I/Q$信号)では,数$%$の振幅誤差や数$°$の位相誤差が無視できません.帯域が$500\mathrm{MHz}$以上では,配線長$10\mathrm{cm}$は長いと考えなければなりません.
MZ-mmCon1の場合
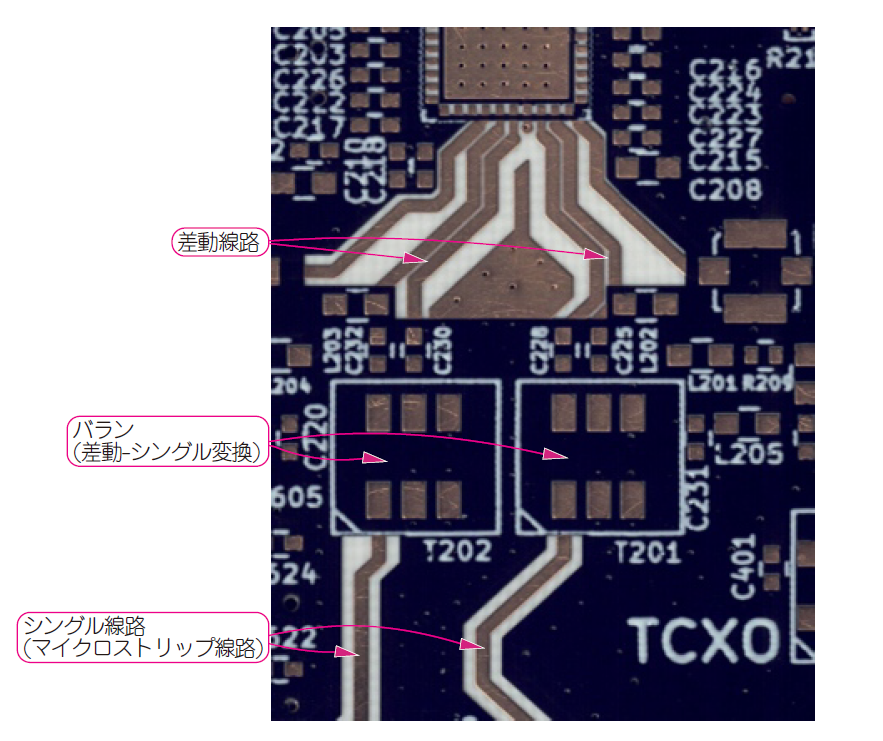
差動タイプのGHz帯のRFデバイス間(MZ-mmCon1のADMV1013やADMV1014)の配線はできるだけ短くします.MZ-mmCon1のベースバンドの入出力信号は帯域が$6\mathrm{GHz}$と広いため,長さが$10\mathrm{mm}$以内の差動線路で接続しています(図E).
「RFデバイスの入出力回路が差動型でせっかく高$SN$比が得られるのだから,そのまま同軸ケーブルでも伝送したい」と考える方もいますが,同軸ケーブルはたいていシングルエンド伝送用です.もし同軸ケーブルを使って差動信号を伝送すると,大きなスキューが発生します.それでも同軸ケーブルで差動信号を伝送したいときは,ベースバンドの信号処理によって調整しなければなりません.
MZ-mmCon1では,バランを使って,シングルエンドのベースバンド入力信号を差動に,差動のベースバンド出力信号をシングルエンドに変換して,同軸ケーブルで伝送しています.
図E MZ-mmCon1のベースバンド信号(帯域$6\mathrm{GHz}$)のプリント・パターンは$10\mathrm{mm}$以下の短い差動線路になっている
コプレーナ線路の使いどころ
MZ-mmCon1では,ミリ波の送受信伝送路はコプレーナ線路です(図F).
$27\mathrm{G}~43\mathrm{GHz}$のミリ波帯では,グラウンド層の入れ替えに利用するビア(VIA)の影響を極力抑えなければなりません.ビアは特性インピーダンスを乱すからです.MZ-mmCon1では,表層にグラウンドが通るコプレーナを選択しました.
線路を挟むベタ・グラウンドには,表層グラウンドと内層グラウンドの間に波長よりもずっと狭い間隔でできるだけ多くのビアを打ち共振の発生を避けます.特定の周波数で共振が発生すると,信号が消失してしまいます.
図F MZ-mmCon1のミリ波($24\mathrm{G}~43\mathrm{GHz}$)の伝送路はコプレーナ線路線路を挟むベタ・グラウンドにはたくさんのビアを打って,共振を抑えている
マイクロストリップ線路の使いどころ
RFデバイスはシングルエンド入出力品が多いため,同じくシングルエンドタイプの線路を選ぶことが多くなります.
図Gに示すのは,アンプ(LO AMP)から抵抗分岐を経て,ミリ波ダウン・コンバータIC(ADMV1014)に至る$6.8\mathrm{G}~10.75\mathrm{GHz}$のローカル信号が伝える線路です.ADMV1014のローカル入力(LO)の反射特性が良くないため,アッテネータ(ATT)を挿入して,その影響を抑えています.
PLLシンセサイザ ADF5356の出力は,$6.8\mathrm{GHz}$以下は差動が選べますが,$6.8\mathrm{G}~13.6\mathrm{GHz}$はシングルエンド出力しかありません.そこで,ADMV1014のローカル信号(LO)入力はシングル入力モードに設定し,ローカル信号(LO)を送信側(TX)と受信側(RX)に分岐する電力分配用の配線には,マイクロストリップ線路を利用しました.
コプレーナ線路でもかまいませんが,前述のようにたくさんのビアを打つことになり,内層の配線の自由度がありません.ビアを使わない配線の自由度の高いマイクロストリップ線路が使えるならそうしたほうが合理的でしょう.
図G ローカル・アンプから抵抗分岐,LO入力にかけての伝送路はマイクロストリップ線路
関連製品・記事
- [KIT]ミリ波5G対応アップ・ダウン・コンバータ MkⅡ(mz-mmcon1後継機)
- [KIT]ミリ波5G対応アップ:ダウン・コンバータ(生産終了品)
- [KIT]実験用800M~6GHz 広帯域90°ハイブリッド
- [KIT]実験用27.5G-29.5GHzバンド・パス・フィルタ
- [KIT]実験用28GHzミリ波パッチ・アンテナ
- [VOD/KIT]GPSクロック・ジッタ・クリーナ
- [VOD]MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
- [VOD/KIT]3GHzネットアナ付き!RF回路シミュレーション&設計・測定入門
- [VOD/KIT]3GHzネットアナ付き!初めてのIoT向け基板アンテナ設計
- [VOD/KIT]初めてのソフトウェア無線&信号処理プログラミング 基礎編/応用編
- [VOD]Pythonで学ぶ マクスウェル方程式 【電場編】+【磁場編】
- [VOD]Pythonで学ぶ やりなおし数学塾1【微分・積分】
- [VOD]Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
- 超長距離無線LoRaからローカル5Gまで!GNU Radio×USRPで作るソフトウェア無線機
DTP:ふじむぅスタジオ
(c)Takashi Kato All Right Reserved.