[技術連載]
5G時代の先進ミリ波ディジタル無線実験室
[Vol.4 信号が減衰しない基板]

次世代高速移動通信と高分解能レーダのキー・テクノロジ

• 著者・講師：株式会社ラジアン（加藤 隆志/Takashi Katou）
• 企画編集・主催： ZEPエンジニアリング株式会社


• 関連製品：［KIT］ミリ波5G対応アップ・ダウン・コンバータ MkⅡ（mz-mmcon1後継機）
• 関連製品：［KIT］ミリ波5G対応アップ：ダウン・コンバータ（生産終了品）
• 関連製品：［KIT］実験用800M～6GHz 広帯域90°ハイブリッド
• 関連製品：［KIT］実験用27.5G-29.5GHzバンド・パス・フィルタ
• 関連製品：［KIT］実験用28GHzミリ波パッチ・アンテナ
• 関連製品：［VOD/KIT］GPSクロック・ジッタ・クリーナ
• 関連製品：［VOD］MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
• 関連製品：［VOD/KIT］3GHzネットアナ付き！RF回路シミュレーション＆設計・測定入門
• 関連製品：［VOD/KIT］3GHzネットアナ付き！初めてのIoT向け基板アンテナ設計
• 関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング 基礎編/応用編
• 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
• 関連記事：超長距離無線LoRaからローカル5Gまで！GNU Radio×USRPで作るソフトウェア無線機

【Index】

• Vol.1　ミリ波の性質と広帯域通信の実験環境
• Vol.2　反射の起こらない線路を作る
• Vol.3　電磁波の漏れが少ない伝送線路
• Vol.4　信号が減衰しない基板
• Vol.5　高周波センスを磨く！スミス・チャート
• Vol.6　部品や伝送線路の入出力特性モデル「$S$パラメータ」
• Vol.7　高速データ伝送 成功の鍵「群遅延」
• Vol.8　初めての28GHzミリ波伝搬実験
• Vol.9　帯域優先？精度優先？2種類の周波数変換方式

超低$C/N$！mz-mmcon1 後継機 z-mmcon2 誕生

写真Aに示すのは，1台でミリ波を使ったディジタル無線通信が可能な$I/Q$変調＆周波数コンバータ“z-mmcon2”(開発：ラジアン)です．ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1の後継機です．

スペック

1. 送信周波数範囲：24.0G～44.0GHz
2. 送信出力範囲：+10～-29dBm（信号の条件 CW）
3. 送信ゲイン範囲：+20～-19dB（$I/Q$動作時）
4. 受信周波数範囲：24.0G～44.0GHz
5. 受信入力範囲-：10dBm以下（信号の条件 CW）
6. 受信ゲイン範囲：+12～-9dB（$I/Q$動作時）
7. 受信雑音指数：10dB以下
8. ベースバンド周波数範囲：DC～100kHz（内蔵D-Aコンバータ，外部アクセス不可）
9. ベースバンド・レベル範囲：0dBm以下（内蔵D-Aコンバータ，外部アクセス不可）
10. IF周波数範囲：1G～6GHz（本体背面のSMA端子）
11. IFレベル範囲：0dBm以下（本体背面のSMA端子）
12. 電源：付属のACアダプタ（DC6V，2A）
13. 消費電流：1.5A（通常動作時）
14. 基板サイズ：128×93×1.6mm（基材はRogers4350B）
15. ケース・サイズ：$W$=140mm $D$=129mm $H$=40mm（フランジ含む）

従来品 ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1からの改善点

z-mmcon2（写真A ）は，従来機のmz-mmcon1から，下記の点が改良されています．

1. 周波数範囲の拡大（27GHz～43GHz → 24GHz～44GHz）
2. シンセサイザICの変更（ADF4372）に伴う$C/N$の大幅改善
3. 制御をWindowsアプリからターミナルに変更（FTDIドライバに起因するトラブル回避）
4. 外部機器との接続をIF（1G～6GHz）だけに変更
5. 放熱ケース採用とファンレス化，ケースの大型化
6. USBマイクロをUSB-Bに変更（コネクタ破壊対策）

高周波信号の伝送は「マッチング」と「減衰対策」

インピーダンス・マッチング処理がなされていない伝送線路では，信号のエネルギが負荷端で吸収されずに反射して送信端に戻ります．受信端もマッチングしていない場合は，そのエネルギは反射を繰り返します．

反射を発生させないためには，送端の出力インピーダンス，受端の入力インピーダンス，および線路の特性インピーダンスを等しくする「マッチング」を施します．この処理をすることで，高周波電力が効率最大で伝わるようになります．

この処理は高周波電力伝送の基本ですが，どんなに完璧にマッチングをしても，「信号の減衰」だけは食い止めることはできません．この減衰は周波数が高くなるほど増して，マイクロ波以上ではマッチング不良よりも問題になることがあります．

減衰の原因は主に次の2つです．

1. 金属の表皮効果による損失
2. 誘電体による損失

これらの損失は，負荷に届く前に線路や誘電体内部で消費され熱に変わります．伝送線路が長くなるほど損失は増し，伝送効率低下の支配的な要因になります．例えば，FR-4基板を伝わる$2\mathrm{G}～3\mathrm{GHz}$の高周波電力は，わずか$10\mathrm{cm}$の線路で$1\mathrm{dB}$以上減衰して無視できません．

損失と反射を小さく抑えることができれば，高周波電力を効率よく伝送できるだけでなく，高速ディジタル信号の波形の乱れを最小限にし，伝送信号の品質指標である「アイ開口」を確保することができます．

本技術解説シリーズ Vol.4では，伝送線路の損失発生のメカニズムとその対策を解説します．

高周波信号の損失要因①「DC抵抗」

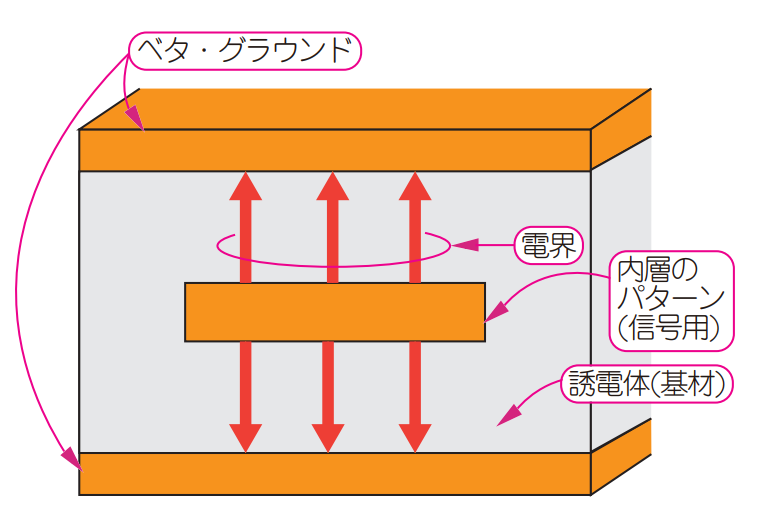
本稿では，ベタ・グラウンドに挟まれた内層に配線されたストリップ線路(図1)を例にして解説します．特に，USBなど，高速ディジタル信号に利用される長めの伝送線路を想定しています．

電源などの低周波回路で，効率を悪化させる「DC抵抗」は，次に説明する表皮効果によってより大きな損失となります．

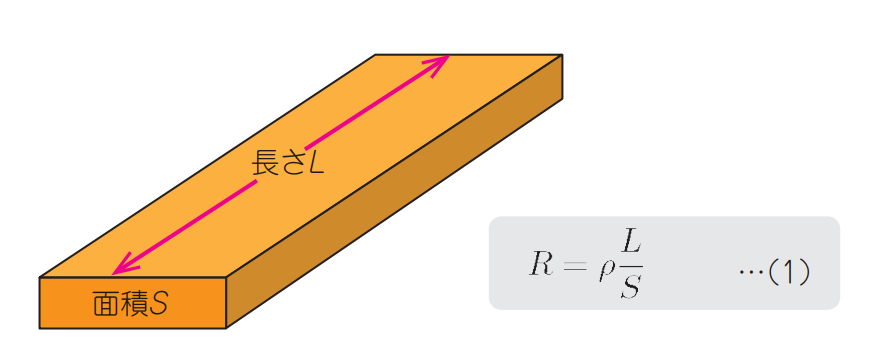
図2に示すのは，断面積$S$ [$\mathrm{m^2}$]，長さ$L$ [$\mathrm{m}$]の金属板で，プリント・パターンを想定しています．

次式は，両断面間の抵抗値を求める式です．

\begin{equation} R=\rho\frac{L}{S} \end{equation}

$\rho \mathrm{[Ωm]}$は，$1$立方メートルあたりの抵抗値「電気抵抗率」です．断面積で割って，長さを掛ければさまざまな形状の抵抗値を計算できます．

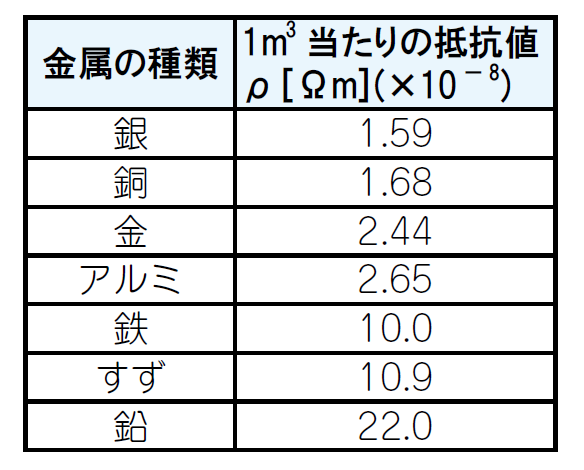
線路幅$0.1\mathrm{mm}$で箔厚$18μm$，長さ$100\mathrm{mm}$のストリップ線路のDC抵抗値は$1\mathrm{Ω}$近くあります．表1に示すように，電気抵抗率は，金属の種類によって固有の値を取ります．プリント・パターンは銅なので，$1.68 \times10^{-8} \mathrm{Ωm}$です．

高周波信号の損失要因②「表皮効果」

減衰の一番の要因

高周波電流は，金属の表面に沿って流れる性質があります．

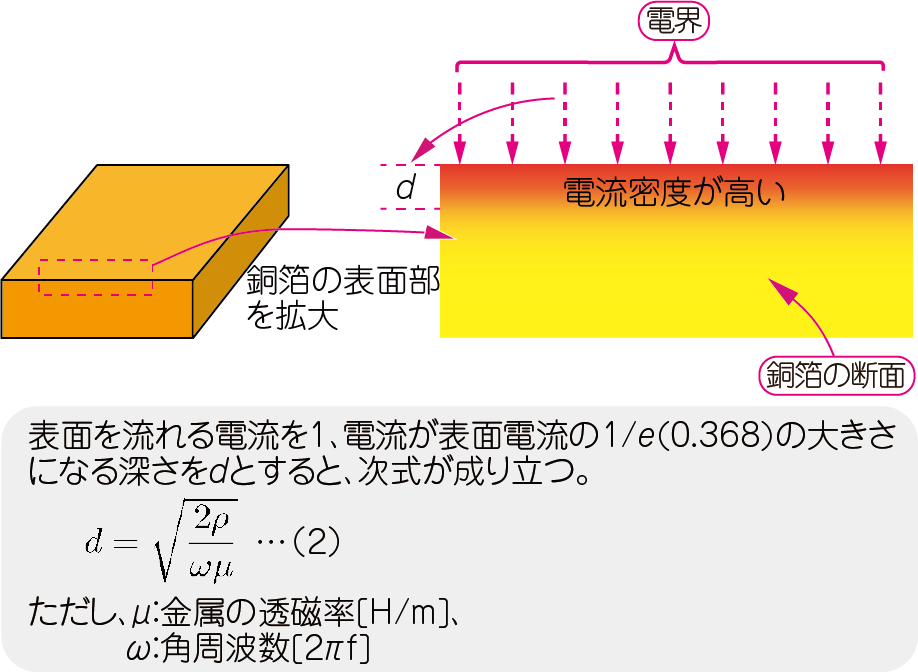
図3に示すのは，高周波電流が流れている金属の表面のようすです．電流は，金属表面に集まり，電界に沿うように分布します．このように高周波では，電界と電流はセットになっています．

電流の密度は表面が一番濃く，金属の内部に入るほど薄まります．この偏りを表す指標を「表皮効果の深さ」と呼び，電流密度が表面の$1/e(=0.368$倍)に薄まる深さで定義します．

表皮効果の深さ($d$)は，次式で表されます．

\begin{equation} d=\sqrt{\frac{2\rho}{\omega\mu}} \end{equation}

$ω=2\pi f$($f$は周波数)ですから，表皮効果の深さ($d$)は周波数の平方根の逆数に比例し，周波数が高くなるほど等価的な断面積($S$)が小さくなって，抵抗値が上がります．

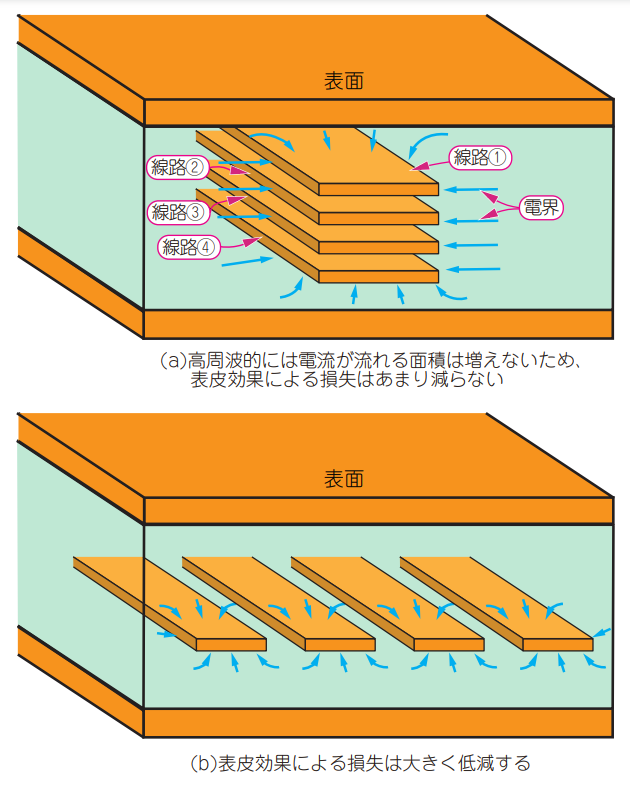
表皮効果による損失は，線路幅を広くすれば表面積が増えるので小さくなります．ただし，図4(a)に示すように，内層の線路を縦積みにしたのでは，DC抵抗は下がっても，電界が存在する面積が増えないので，表皮効果の改善効果は限定的です．線路幅を広くするなら，図4(b)に示すように，電界が存在する面積が増えるように横並びにしたほうがよいでしょう．

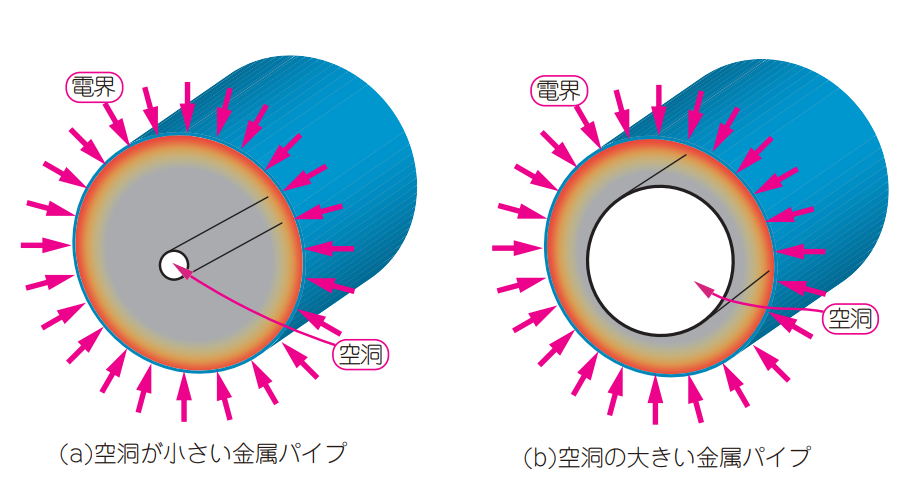
図5に示すのは銅パイプの例です．図5(b)に示すように，空洞を減らして導体部のボリュームを増すとDC抵抗は下がりますが，電界が存在する面積が増えないので表皮効果の改善効果はほとんどありません．

表皮効果は10MHz以上で現れる

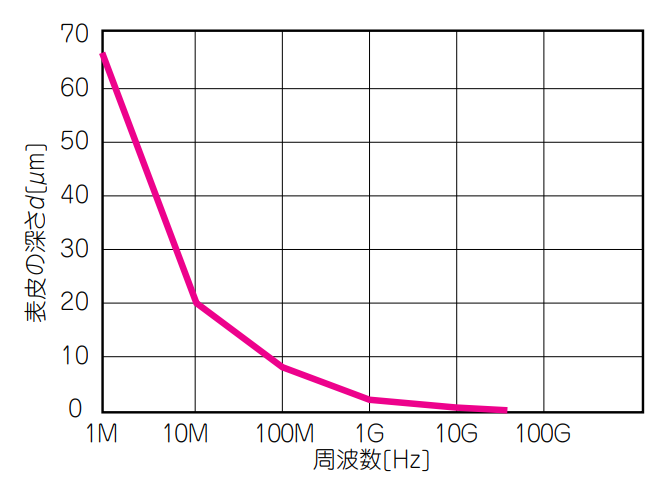
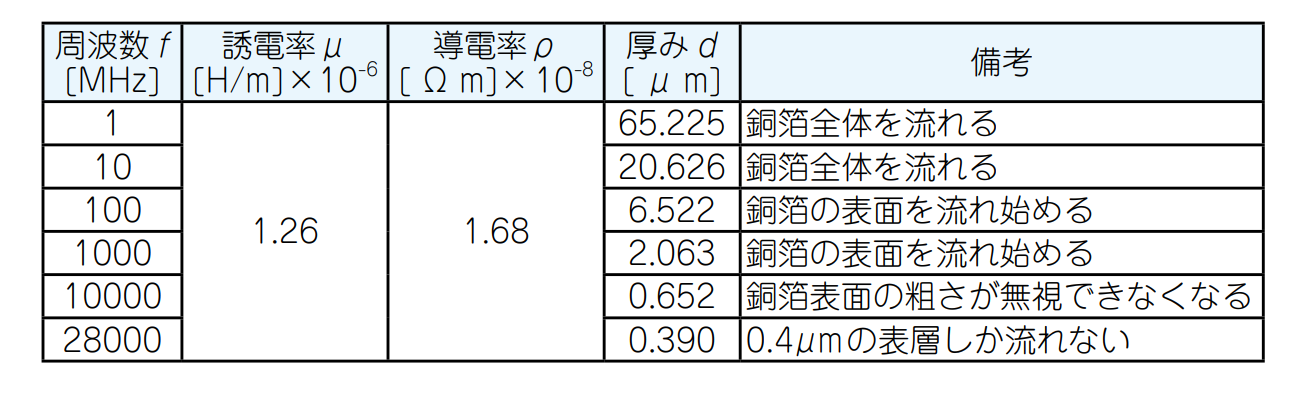
図6と表2に示すのは，表皮効果の深さと周波数の関係です．

$10 \mathrm{MHz}$以下の電流は，$20\mathrm{μm}$以上の深さを流れます．通常，プリント基板の銅箔の厚みは$18 \mathrm{μ}$ ～ $35 \mathrm{μm}$ですから，電流は銅箔の断面全体をほぼ一様に流れます．

$1 \mathrm {GHz}$を超えると表皮効果が顕著になり，電流は表面から$2 \mathrm{μm}$以下の部分に集中します．

$28 \mathrm{GHz}$では，わずか$0.4 \mathrm{μm}$の深さに電流が集中しますから，金属表面の傷や荒れが損失に効いてきます．無電解金フラッシュは，金の厚さが約$0.03 \mathrm{μm}$ととても薄く，$28 \mathrm{GHz}$程度の高周波電流であれば，金の層を無視して全体が銅でできていると考えて計算しても問題ないでしょう．

減衰量は周波数の平方根に比例して増える

次に示すのは，周波数$f[\mathrm {GHz}]$での減衰量$[\mathrm{dB}]$を求める近似式です．なお，$R_{DC}$は線路のDC抵抗$[Ω]$で，$Z_0$は特性インピーダンス$[\mathrm{Ω}]$，$t$は線路の厚さ$[\mathrm{mm}]$，$f$は周波数$[\mathrm{GHz}]$とします．

\begin{equation} L_m=-2.08 \times 10^6 \times \frac{R_{DC}}{Z_0}t\sqrt{f} \end{equation}

式(3)から，銅箔の厚さ($t$)が大きいほど減衰が増すように見えますが，$R_{DC}$は$t$に反比例するため，$t$は打ち消されます．

$R_{DC}$＝$\rho/(Wt)$と書き換えると，次のようになります（ただし，$t\gg d$とする）．

\begin{eqnarray} L_m=-2.08 \times10^6 \times \left(\frac{\rho L \sqrt{f}}{Z_0W}\right) \end{eqnarray}

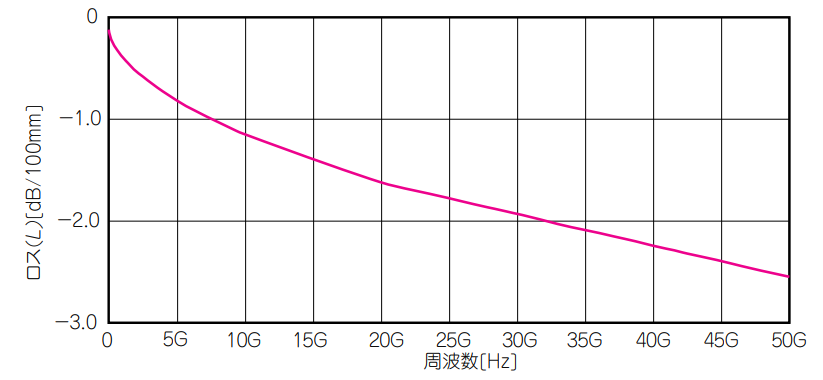
図7に，表皮効果による線路長$100 \mathrm{mm}$あたりの減衰量の周波数特性を示します．このように減衰量は，周波数の平方根に比例して増します．

高周波信号の損失要因③「誘電損失」

誘電体の寄生抵抗成分による損失

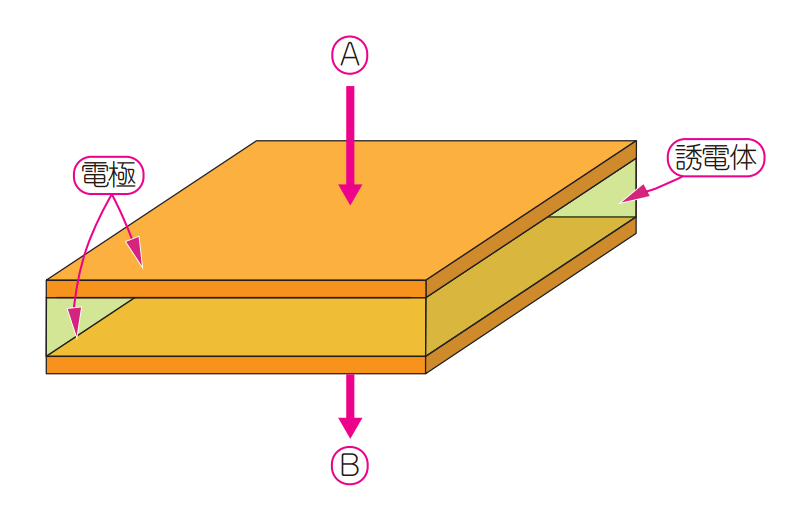
図8に示すベタ・グラウンドがはさむ誘電体が理想的ならば，このプリント基板は純粋なリアクタンス性を示します．まったくエネルギを消費せず，損失はゼロです．これは理想的なコンデンサやインダクタと同様です．

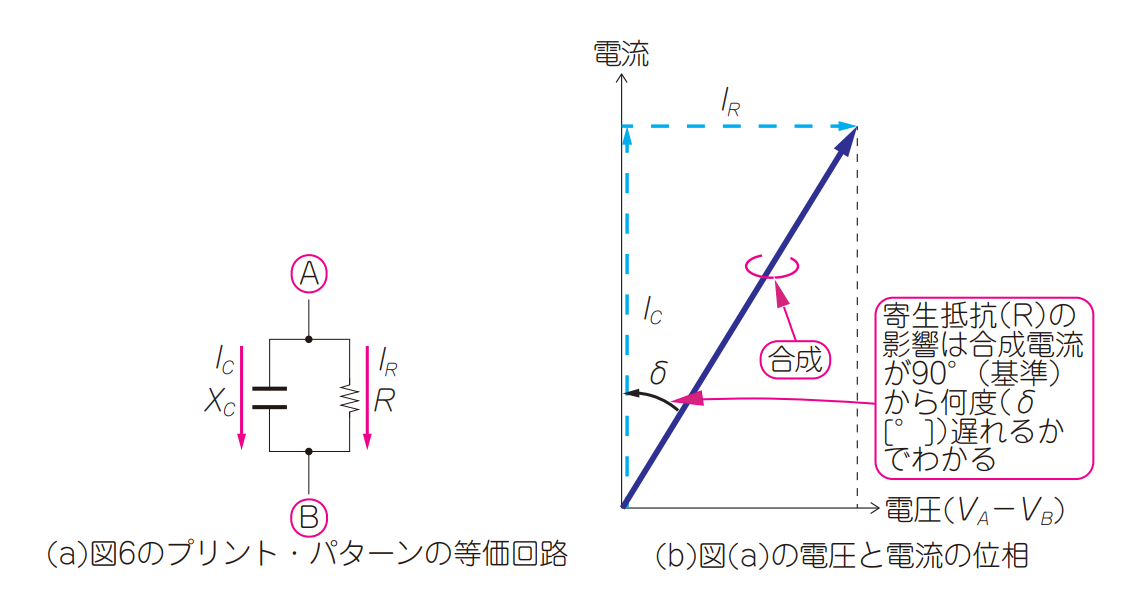
実際の基板は，図9(b)の等価回路で表され，リアクタンス成分($X_C$)と並列に抵抗成分($R$)が寄生しています．この抵抗成分($R$)を誘電損失と呼び，損失の要因になります．コンデンサの寄生抵抗($R$)は，等価直列抵抗($ESR$，Equivalent Series Resistance)と呼ばれていて，周波数によってその値が変動します．

図9(a)のリアクタンス($X_C$)に流れる電流($I_C$)は，入力電圧に対して$90^{\circ}$位相が進みますが，寄生抵抗($R$)を流れる電流($I_R$)は電圧と同相です．

実際に流れる電流は，$I_C$と$I_R$が合成されたもので，$\delta[^{\circ}]$位相が遅れます．$\delta$の正接($\tan$)を誘電正接と呼びます(タンデルタとも言う)．式で表すと次のようになります．

\begin{equation} \tan{\delta}=\frac{I_R}{I_C}=\frac{X_C}{R}=\frac{1}{Q} \end{equation}

これはコンデンサやインダクタの性能を表すパラメータ「クオリティ・ファクタ($Q$)」の逆数です．最も広く利用されているプリント基板の材料 FR-4の$\tan(\delta)$は，$0.01$です．「純粋なリアクタンス成分$1$に対して，抵抗成分による影響(アドミタンス)が$0.01(=1％)$あり，位相が $\delta=\arctan(0.01)＝0.57^{\circ}$ 遅れる」と考えます．

減衰率を求める式

次に示すのは，ストリップ線路の誘電損失による減衰率$[\mathrm{dB/m}]$を求める近似式です．これに長さ$L[\mathrm{m}]$を乗じると，減衰量$[\mathrm{dB}]$が得られます．

\begin{equation} L_d=-91 \tan{\delta} \sqrt{\varepsilon_r}f \end{equation}

式(7)から，誘電損失は誘電正接($\tan(\delta)$)と周波数($f$)に比例し，誘電率($\varepsilon$)の平方根に比例することがわかります．

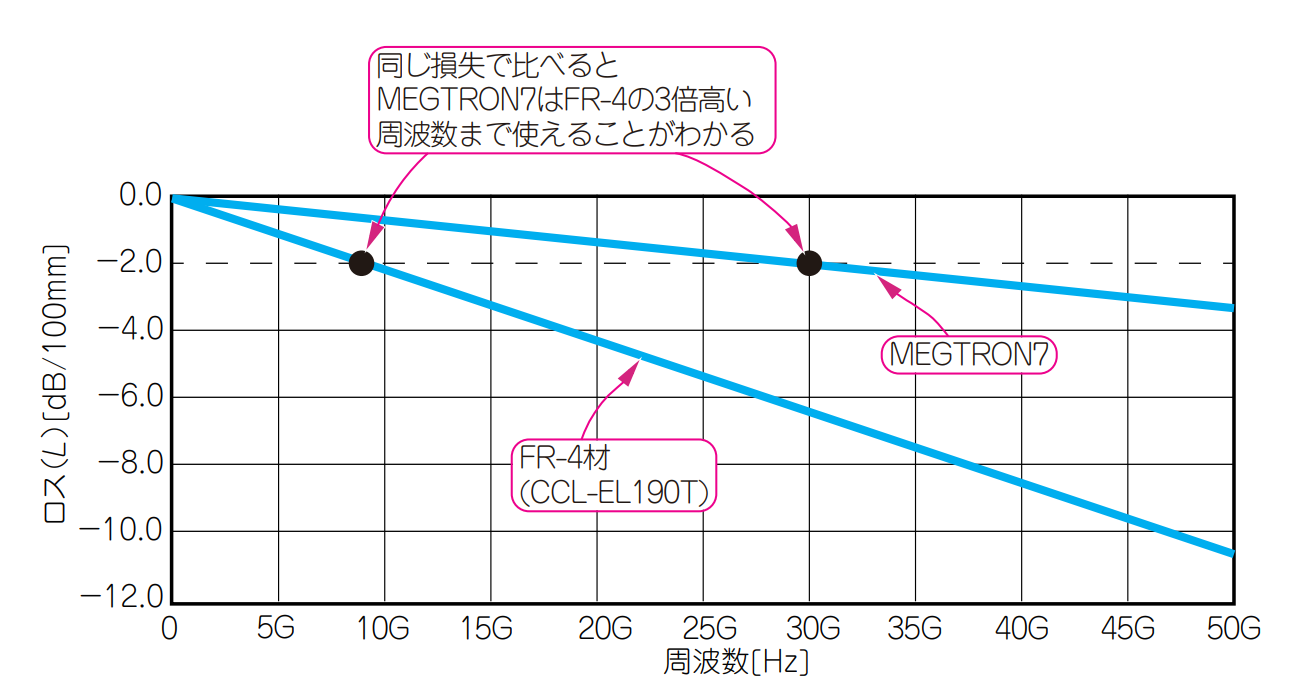
図10に示すのは，$2$種類のプリント基板(FR-4材とMEGTRON7材)の誘電損失の周波数特性です．MEGTRON7は，ミリ波などの高周波基板に利用されている低誘電率材で，誘電正接($\tan(\delta)$)はFR-4の$1/10$です．

誘電正接($\tan(\delta)$)や比誘電率($\varepsilon_r$)には周波数特性があるため，カタログに掲載されている特性グラフを外挿(捕外)して，数値を推測しました．

MEGTRON7は，同じ損失で比べると，FR-4の3倍も高い周波数まで使えることがわかります．式(7)から明らかになように，この違いの要因は．誘電率ではなく誘電正接($\tan(\delta)$)です．MEGTRON7の誘電正接($\tan(\delta)$)は$0.001～0.002$で，FR-4($0.01～0.04$)の$1/10$です．一方誘電率は，FR-4が$4.5～4$，MEGTRON7が$3.3～3.5$で，あまり変わりません．

表皮効果による損失と誘電損失の合算

低誘電率材MEGTRON vs 汎用材 FR-4

図11に示すのは，表皮効果による損失$[\mathrm{dB}]$と誘電損失$[\mathrm{dB}]$を合算した損失の周波数特性です．誘電率は，線路幅によって変わるので，FR-4もMEGTRON7も線路幅($W$)を$0.1\mathrm{mm}$として比べました．MEGTRON7はFR-4より圧倒的に低損失です．

層間の厚さを一定，かつ特性インピーダンス $50\mathrm{Ω}$という現実的な条件で比較すると，低誘電率のMEGTRON7はFR-4よりパターン幅が広くなってDC抵抗が下がり，FR-4より有利です．

汎用材「FR-4」は何Hzまで使える？

許容できる損失や扱える上限周波数は，配線長によって変わります．

図11から，伝送線路長が$10～20\mathrm{cm}$で，損失を$1\mathrm{dB}$(電圧振幅で$10\%$減衰)まで許容するなら，周波数の上限は$1\mathrm{G}～2\mathrm{GHz}$です．

これは経験からも妥当な数字で，ある程度の大きさの基板($20\mathrm{cm}$以上)では，$1\mathrm{GHz}$以上の周波数を扱うときは，FR-4ではなく，MEGTRON6/MEGTRON7(パナソニック製)，RO4350(Rogers製)を使っています．

ディジタル信号の伝送波形をExcelで予測

無線よりもディジタル伝送のほうが基板ロスの周波数特性の影響が大きい

図11に示すように，プリント基板のロスの周波数特性は，縦軸をログ・スケール$[\mathrm{dB}]$としたとき，右肩下がりの直線になります．

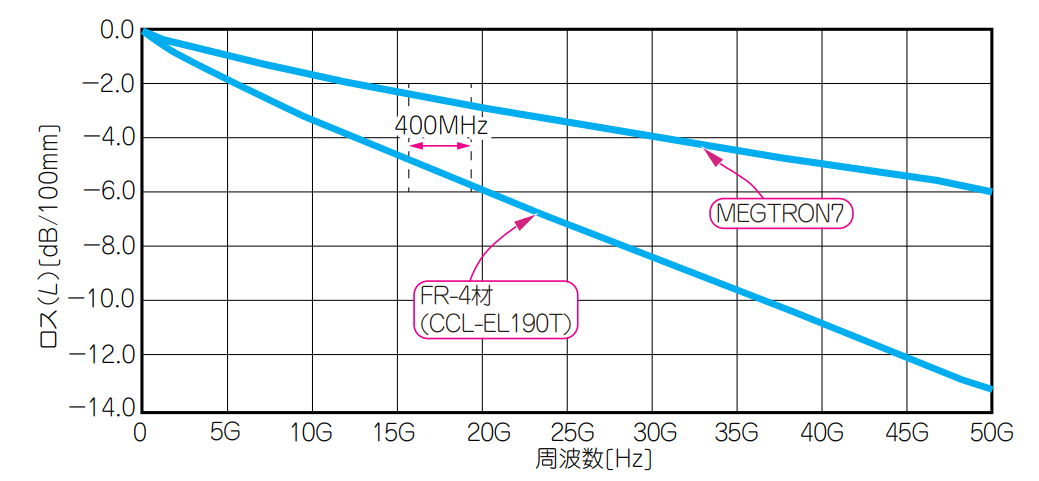
無線通信システムは，キャリア周波数(中心周波数)が数十$\mathrm{GHz}$と高くとも，帯域はせいぜい数百$\mathrm{MHz}$です．これを図11のプリント基板のロスの周波数特性に照らすと，数百MHz程度の帯域では基板のロスの影響をあまり受けないことがわかります．次世代5Gが超広帯域($400\mathrm{MHz}$)だといっても，その周波数範囲でのロスの周波数変化はなく，一定値と考えても問題ありません．

ところが，$\mathrm{Gbps}$クラスの高速ディジタル信号は，DC付近から数十$\mathrm{GHz}$にまで，スペクトルが広帯域に分布するため，右肩下がりの周波数特性の影響を強く受けます．具体的には，ディジタル信号の波形が鈍って波高値が下がり，結果としてアイ開口が狭くなり，$BER$(Bit Error Rate)が悪化します．

基礎知識…矩形波の周波数成分

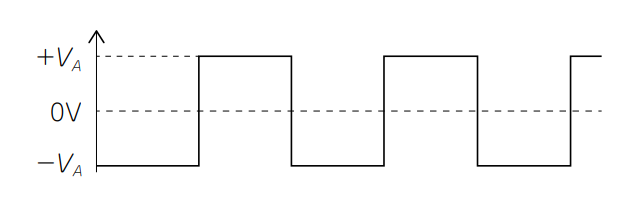
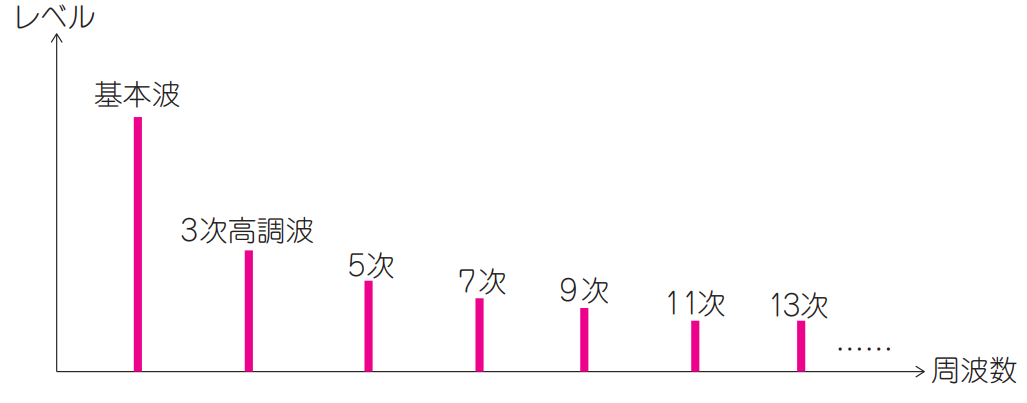
次式のように，図12に示す矩形状のディジタル信号は，周波数成分の合成で表すことができます．この式をフーリエ級数展開と呼び，繰り返し波形ならどんなに複雑でも，正弦波の合成で表すことができます．図で表すと図13のようになります．

\begin{equation} y(t)=\frac{4A}{\pi}\left( \sin{(\omega t)}+\frac{1}{3}\sin{(3\omega t)}+\frac{1}{5}\sin{(5\omega t)…}\right) \end{equation}

逆に言えば，高次高調波のレベルを調節することで，どんな波形も合成できます．実際，Excelに式(8)を入力して，高次高調波を加算してみると，図12の矩形波が合成されます．$2$次以上の高調波のレベルを変えると，矩形波は三角状になったり，スパイク状になったりします．また，偶数次高調波を加えると，上下非対称の波形になります．

基板のロスの影響は伝送波形に現れる

伝送線路の周波数特性がわかっていれば，矩形波を入力したとき，どんな波形になって出てくるかを計算で予測することができます．

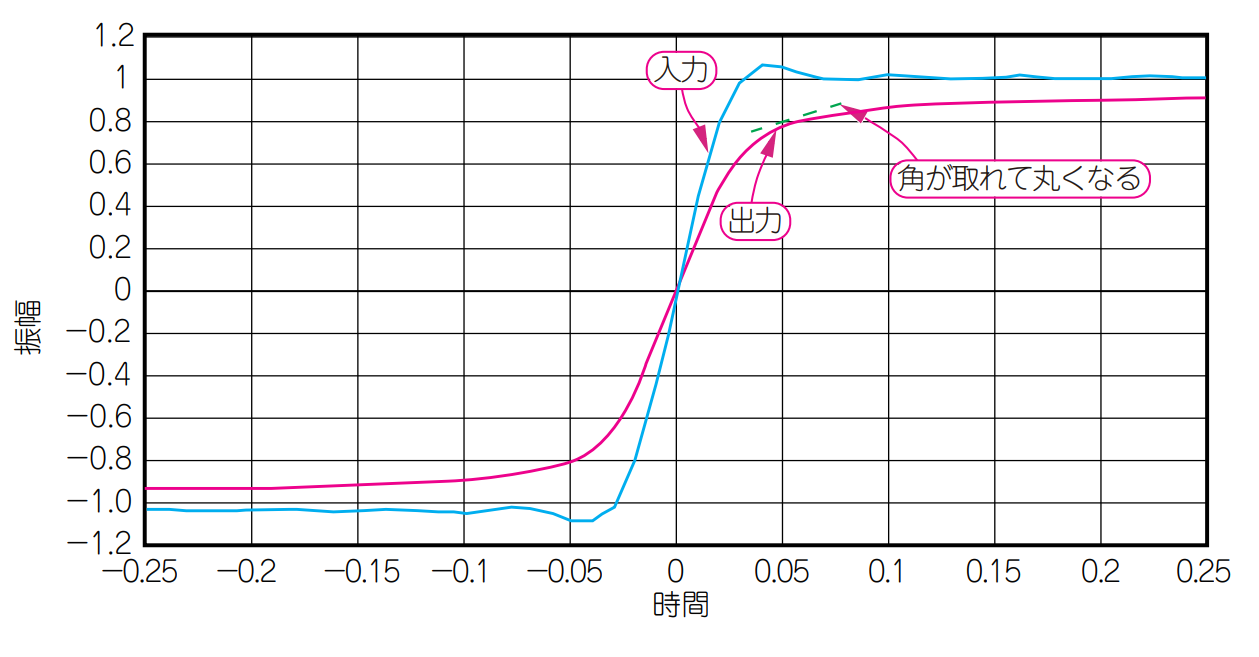
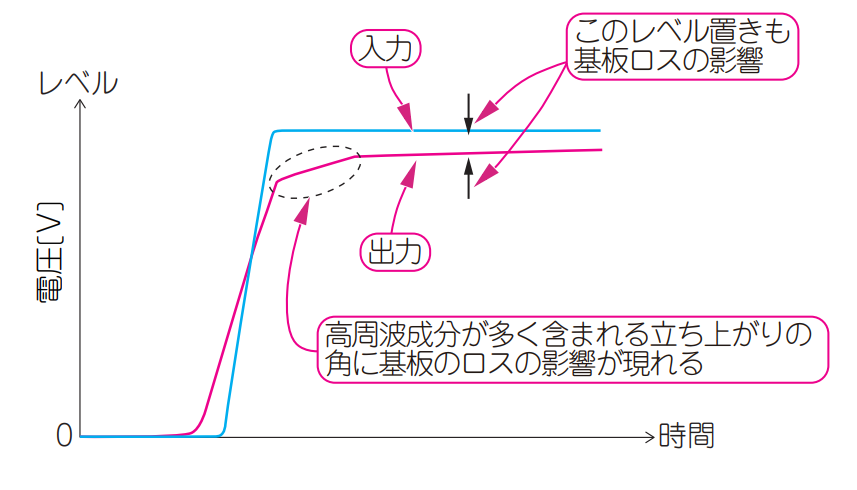
図14に示すのは，ある伝送線路にステップ信号を入力し，出力される波形をExcelで計算した結果です．図15は，この波形の特徴を強調して模式的に表したものです．

実際，図14の入力信号が図11に示したロス特性をもつ伝送線路(FR-4，長さ$100\mathrm{mm}$)を通過すると，同じく図14の出力信号のような波形に変化します．この出力信号は，入力ステップ信号の高調波スペクトルの係数(信号の大きさ)と，図11で求めたFR-4(長さ$100\mathrm{mm}$)の各周波数の減衰率を乗算し，新たな高次高調波と基本波を加えて求めました．

図14の出力信号を見ると，入力信号より立ち上がり時間($t_R$)と立ち下がり時間($t_F$)が長くなっています．よく見ると，立ち上がりの角が切り取られたような形状になっていて，波高も$100\%$に届かず，$90\%$に収束しています．

このことから，基本波($3\mathrm{GHz}$)での伝送ロスが$1\mathrm{dB}$($10％$)あることがわかります．実際に基板を製作して，高速ディジタル信号を評価すると，上記の計算結果に近い波形が観測されるはずです．

このように，基板のロスの影響は，伝送線路を通過した信号の立ち上がりの角と波高に現れます．

[参考]図14の入力のステップ信号の合成方法

ここで，図14の入力信号をどのようにして合成したのか説明しましょう．

シャープなステップ波形を得るためには，無限次までの高調波を加算すればよいのですが，現実的ではありませんから，$15$次以下の高調波を加算しました．

さらに，単純な加算では$20\%$もの大きなリンギングが生じるため，コサイン型のナイキスト・フィルタを掛けて抑え込みました．このフィルタは，基本波で$1$を，$17$次で$0$を乗算する窓関数です．合成されたステップ信号は，$15$次までの高調波を含んでいます．図13の基本波の周波数を$3\mathrm{GHz}$とすると，$15$次は$45\mathrm{GHz}$にもなります．

なお，図14に示す波形は計算で得たものですが，これを測定器を使って精度良く観測するためには，分解能が数$\mathrm{ps}$，帯域が約$100\mathrm{GHz}$のサンプリング・オシロスコープが必要です．しかし，そのような高価な測定器がなくても，Excelを使って波形を予測し，マッチングをとることは可能です．ただし，実際の伝送線路は，反射の影響が大きいため，最終的なアイ開口までは求められません．

(c)Takashi Kato