5G時代の先進ミリ波ディジタル無線実験室[Vol.6 部品や伝送線路の入出力特性モデル「$S$パラメータ」]
次世代高速移動通信と高分解能レーダのキー・テクノロジ
- 著者・講師:株式会社ラジアン(加藤 隆志/Takashi Katou)
- 企画編集・主催: ZEPエンジニアリング株式会社
【Index】
- Vol.1 ミリ波の性質と広帯域通信の実験環境
- Vol.2 反射の起こらない線路を作る
- Vol.3 電磁波の漏れが少ない伝送線路
- Vol.4 信号が減衰しない基板
- Vol.5 高周波センスを磨く!スミス・チャート
- Vol.6 部品や伝送線路の入出力特性モデル「$S$パラメータ」
- Vol.7 高速データ伝送 成功の鍵「群遅延」
- Vol.8 初めての28GHzミリ波伝搬実験
- Vol.9 帯域優先?精度優先?2種類の周波数変換方式
ミリ波通信実験用アップ・ダウン・コンバータ mz-mmCon1を例に,$27\mathrm{G}~40\mathrm{GHz}$の超高周波「ミリ波」を伝送する基板や回路の設計技術を解説します.〈ZEPマガジン〉
[PR]従来の測定器でミリ波実験!周波数変換アダプタ・キット z-mmcon2
写真Aに示すのは,1台でミリ波を使ったディジタル無線通信が可能な$I/Q$変調&周波数コンバータ“z-mmcon2”(開発:ラジアン)です.ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1の後継機です.
<a “=”” href=”https://www.zep.co.jp/wp-content/uploads/2026/01/p0.png”>  |
|---|
| 写真A 1台でローカル5Gのミリ波無線通信の実験が可能なアップ・ダウン・コンバータ z-mmcon2(mz-mmcon1のC/Nを大幅に改善した後継機 (開発:株式会社ラジアン) |
- 送信周波数範囲:24.0G~44.0GHz
- 送信出力範囲:+10~-29dBm(信号の条件 CW)
- 送信ゲイン範囲:+20~-19dB($I/Q$動作時)
- 受信周波数範囲:24.0G~44.0GHz
- 受信入力範囲-:10dBm以下(信号の条件 CW)
- 受信ゲイン範囲:+12~-9dB($I/Q$動作時)
- 受信雑音指数:10dB以下
- ベースバンド周波数範囲:DC~100kHz(内蔵D-Aコンバータ,外部アクセス不可)
- ベースバンド・レベル範囲:0dBm以下(内蔵D-Aコンバータ,外部アクセス不可)
- IF周波数範囲:1G~6GHz(本体背面のSMA端子)
- IFレベル範囲:0dBm以下(本体背面のSMA端子)
- 電源:付属のACアダプタ(DC6V,2A)
- 消費電流:1.5A(通常動作時)
- 基板サイズ:128×93×1.6mm(基材はRogers4350B)
- ケース・サイズ:$W$=140mm $D$=129mm $H$=40mm(フランジ含む)
1.定石!$S$パラメータで回路や部品をモデリング
理由1:動作条件による回路や部品の特性変化が大きい
バイポーラ・トランジスタを使った昔ながらの低周波用ディスクリート・アンプは,バイアス電流の設定値によって,周波数特性やゲイン,ひずみ,入力レンジなどの基本性能が大きく変化します.この初期設定による特性の変化の問題を解決したのがOPアンプです.10石以上のトランジスタを組み合わせて,100dB以上のゲインをもつアンプを構成し,フィードバックをかけることで,電源電圧や電源雑音の影響を受けにくい,使い勝手の良さを実現しています.
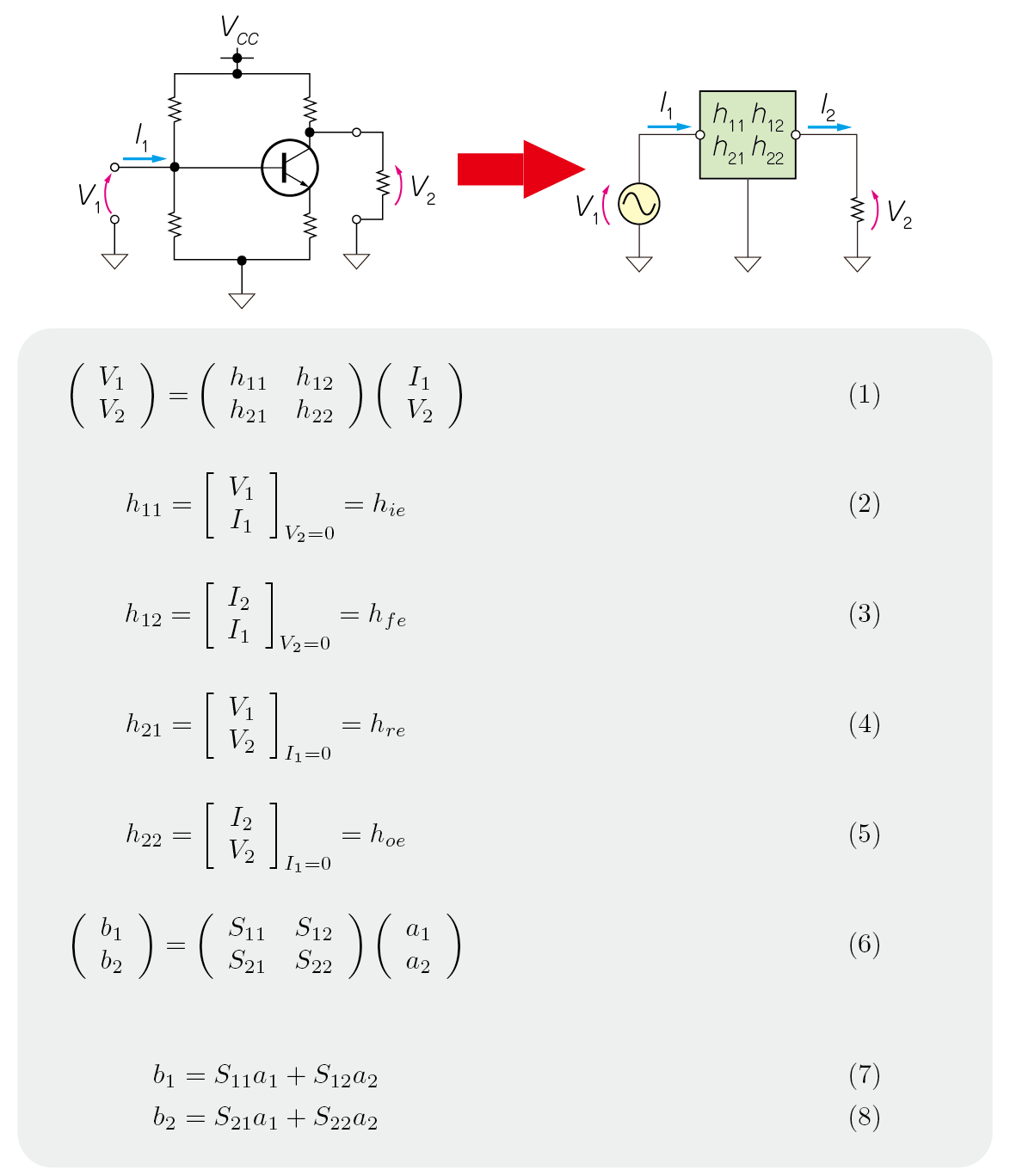
OPアンプがなかった時代は,トランジスタ回路の入出力特性をパラメータ($h$パラメータなど)でモデル化して,計算による設計をしていました(図1).高周波では,トランジスタのゲインが大きくとれないため,OPアンプのように使える便利なICはなく,電源電圧などの初期条件によって回路や部品の特性が大きく変化します.そこで,低周波のディスクリート・アンプのように,4つのパラメータ($S$パラメータ)を使って,デバイスや回路をモデリングしています.
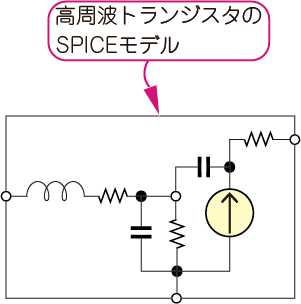
インターネット普及前,メーカは分厚いデータブックにデバイスのスペックを掲載していましたが,現実,使える用紙に限度があるため,示されているのは特定の動作条件における特性値だけでした.4.2Vの電源電圧で使用したいけれど,5Vのときの特性しか掲載されていないときは,ベクトル・ネットワーク・アナライザなど大がかりな測定器や整合用の基板をわざわざ作って$S$パラメータを測定しなおし,等価回路を導いて(図2),計算による精度の高い設計を試みていました.しかし,$S$パラメータの測定には,同軸コネクタとデバイスをインターフェースする基板を製作し,その基板の特性分を測定結果から差し引くなど,その作業は困難を極めます.
現在は,RFデバイスのデータシートに,さまざまな初期条件における$S$パラメータが掲載されています(後述の表1).自分の使用条件に合った$S$パラメータを探して回路シミュレータにモデルとして取り込んで計算すれば,簡単に精度の高い特性予測が可能です.
 |
|---|
| 図2 高周波デバイス・メーカが提供する特性データが十分でなかった時代は,自分で$S$パラメータを実測して等価回路を導いていた |
| 今は,メーカがさまざまな条件(周波数や電源電圧)における詳細な$S$パラメータがテキスト・データで提供されている(表1).現代は,シミュレータ(無料で実用性の高いものも多い)に,これらの$S$パラメータを読み込んで設計するべき |
理由2:電流と電圧の比であるインピーダンスに位相が必要になるぁら
電子部品の大きさが信号の波長より十分小さい低周波でも,回路や部品に信号が入射すると,わずかな時間差で反射は発生しています.しかし信号が変化する時間が,反射波の影響がでる時間より十分に長いため,回路や部品の内部では進行波も反射波も交じり合い安定していて進行波と反射波が瞬時に定常状態に落ち着くため,電圧と電流が一様になっています.そのため,定常化した電圧と電流の比,つまり「インピーダンス」で,部品や回路の特性を表わすことができます.
高周波では,信号の波長(位相)に対して,部品や回路内部の大きさが無視できません.すると部品や回路内部の電圧と電流が一様ではなくなり,前述の直流的なインピーダンスでは,部品や回路の特性を表すことができません.高周波では,入力と出力の進行波と反射波の振幅と位相の関係を表す$S$パラメータで,部品や回路の固有の特性を表すのが定石です.
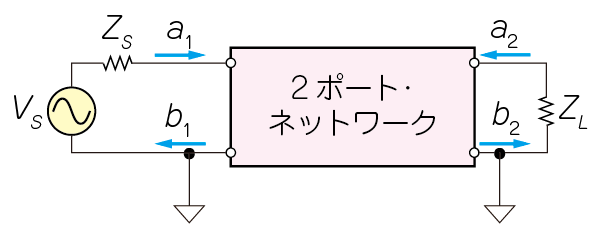
図3に示すように,2つの進行波 $a_1$,$a_2$と反射波$b_1$,$b_2$を考え,進行波と反射波の関係を図中の式(A)のように表します.
 |
|---|
| 図3 $S$パラメータは入力と出力の進行波と反射波の関係を表す |
| 回路の物理的なサイズに対して波長が無視できない高周波では,信号が変化する時間が,反射波の影響がでる時間より短いため,回路や部品,伝送線路の内部で,進行波と反射波が分離している |
2ポート・ネットワークのインピーダンスを$Z_L$に一致させると,終端の反射がなくなります.つまり$a_2=0$となって,$S_{11}$=$b_1$/$a_1$と求まります.このように,2ポート・ネットワークの両側の回路のインピーダンスによって,反射波の大きさが変わるので,$S_{11}$~$S_{22}$の$S$パラメータは,低周波のように部品単体ではなく,周辺の回路に左右されます.
Vol.6は,この$S$パラメータの実際の使い方を実験を交えて解説します.〈ZEPマガジン編集部〉
前回(Vol.5)は,高周波における回路や部品のインピーダンス「特性インピーダンス」や「反射」の影響を定量的に捉えるツール「スミス・チャート」が,高周波信号を効率よく伝えるためにいかに有効なツールかを示しました.この便利なチャートがパフォーマンスを発揮するのは,信号源と部品や回路のインピーダンスが既知なことが前提です.
高周波ではどんなICも部品も,メーカが公開しているインピーダンスは「$S$パラメータ」で表されています.低周波のICや部品のように,位相情報をもたない入力インピーダンスとか出力インピーダンスではありません.高周波シミュレータが備えるモデルの特性も,$S$パラメータで表現されています.
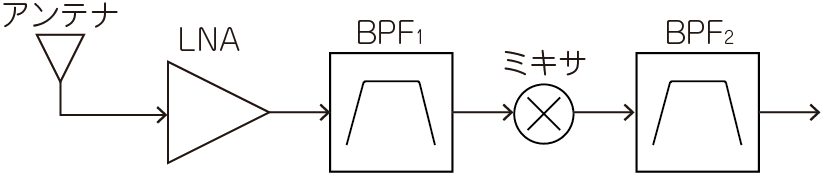
実際,アンテナやアンプ,フィルタ,ミキサ,伝送路,コネクタなど,高周波システムを構成する全要素を$S$パラメータでモデリングしてシミュレーションすることで,実際の回路の特性を予測することができます(図4).最近は,チップ・インダクタやチップ・キャパシタのような表面実装部品まで$S$パラメータが公開されているので,容易に精度の高い設計が可能です.
2.$S$パラメータの基礎
$S$パラメータの値の基準は50Ω
$S$パラメータを利用するのは,一般にUHF(300MHz)以上です.この周波数帯では,基準となるインピーダンスを50Ωに統一して測定するのが定石です.
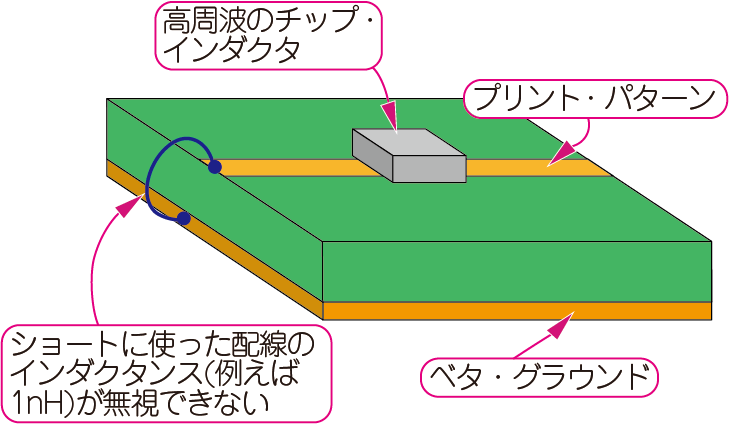
低周波回路では,ショートやオープンなど極端な条件下で動かしてパラメータを測定しますが(図1),GHzを超える高周波では,少しの配線が無視できないインダクタンスをもっているため,そのような極端なインピーダンスを実現できません(図5).これが50Ωなどのインピーダンスを基準にする理由の1つです.本連載が扱うミリ波でも50Ωを基準に,この値からの差分を設計に利用します.
50Ωが選ばれた理由は,ポリエチレン(比誘電率は2.2)を絶縁層にした同軸ケーブルの表皮効果による損失がもっとも小さくなる特性インピーダンスが51Ωだからと言われています.
 |
|---|
| 図5 GHzを超える高周波ではショート(0Ω)やオープン(∞Ω)という極端な条件を実現できないため,50Ωを基準に設計するのが常識である |
| 高周波では,正確なオープン条件やショート条件を実現することは不可能である |
$S$パラメータの定義式
$S$パラメータは,50Ωで整合された信号源や負荷を回路(ブラックボックス)に接続し,回路を通過する信号や入力端で反射する信号の振幅と位相を調べます(図6).この測定をポートをさまざまに組み合わせて,周波数ごとに並べたものが$S$パラメータです.
2ポート・ブラックボックスの$S$パラメータ($S_{11}$,$S_{21}$,$S_{12}$,$S_{22}$)は,次のように表すことができます.ポート数が増えても同様です.仮に3ポートの$S$パラメータの場合,3×3の行列 $S_{11}$~$S_{33}$になります.
ここで,$a_1$は$\mathrm{P}_1$に入力される信号の振幅,$a_2$は$\mathrm{P}_2$に入力される信号の振幅,$b_1$は$\mathrm{P}_1$から出力される信号の振幅,$b_2$は$\mathrm{P}_2$から出力される信号の振幅です.
$S_{11}$は,入力側の反射の度合いを意味しており,小さいほど望ましいパラメータです.$S_{21}$は,アンプなら通過ゲインを意味し,必要な値に近いほど望ましいパラメータです.$S_{12}$は,アイソレーションを意味し,小さいほど望ましいパラメータです.$S_{22}$は,出力側の反射を意味し,小さいほど望ましいパラメータです.
$S$パラメータの測定と意味
$S_{11}$と$S_{21}$
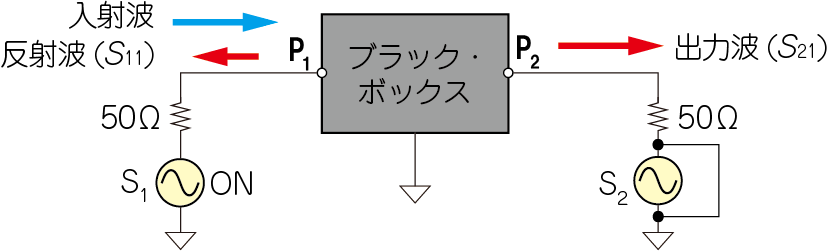
図7に示すように,信号源$\mathrm{S}_1$から,連続波(CW,Constant Wave),またはチャープ信号(周波数スイープ信号)を出力し,$\mathrm{S}_2$は停止させます.$\mathrm{P}_1$と$\mathrm{P}_2$における信号の振幅と位相を同時に測定します.
 |
|---|
| 図7 入力の反射率($S_{11}$)とゲイン($S_{21}$)の測定回路 |
| 信号源$\mathrm{S}_1$をON,$\mathrm{S}_2$をショートして,$S_{11}$と$S_{21}$の振幅と位相を測定する |
$S_{11}$は,進行波を除いて反射して戻ってきた信号だけの振幅と考えることができ,$\mathrm{P}_1$の位置で,不整合による反射波の振幅と位相の比を測ると求まります.$\mathrm{P}_2$の位置で,通過した信号の振幅と位相を測ると,$S_{21}$が求まります(図7).
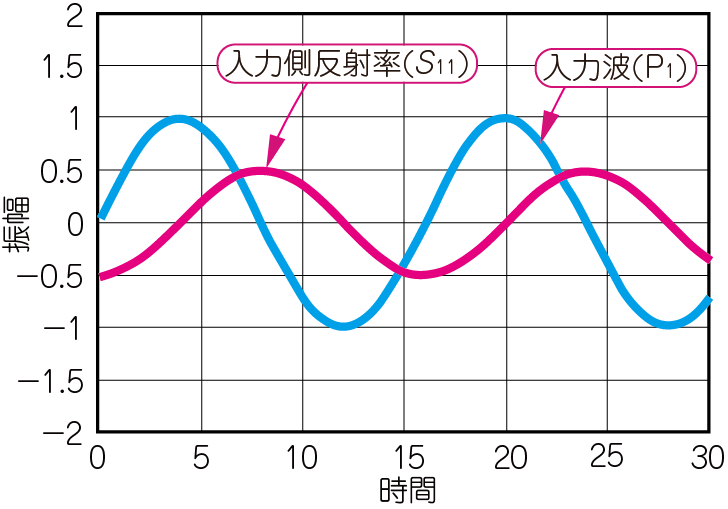
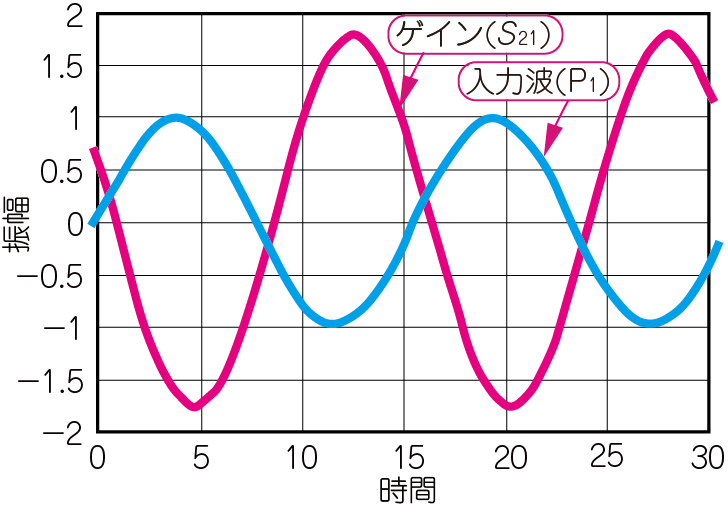
図8に$S_{11}$と$S_{21}$の測定結果を示します.
図8(a)の$S_{11}$の波形を見ると,$\mathrm{P}_1$の位置の電圧は$\mathrm{S}_1$の出力振幅の半分,位相は90°遅れています.この結果から,$\mathrm{P}_1$から見たこのデバイスは容量性であることがわかります.この状態は整合がとれていません.整合を完全に取ると,$S_{11}$の振幅はゼロになります.
図8(b)の$S_{21}$の波形を見ると,振幅は信号源$\mathrm{S}_1$の出力電圧の2倍に,位相は180°反転しています.この結果から,ブラックボックスの中身は,反転型アンプだろうと推定できます.
GHz帯の高周波回路の$S_{11}$を実際に測定するときは,マイクロストリップ・ラインを使った方向性結合器で進行波と反射波を分離します.
$S_{12}$と$S_{22}$
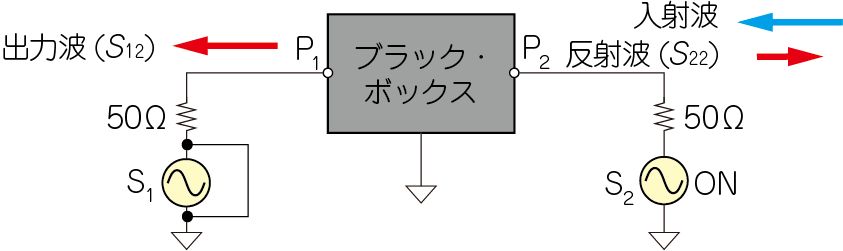
図9に示すように,信号源$\mathrm{S}_2$から,連続波(CW,Constant Wave),またはチャープ信号(周波数スイープ信号)を出力し,$\mathrm{S}_1$は停止させます.$\mathrm{P}_1$と$\mathrm{P}_2$における信号の振幅と位相を同時に測定します.
 |
|---|
| 図9 アイソレーション($S_{12}$)と出力の反射率($S_{22}$)の測定回路 |
| 信号源$\mathrm{S}_2$をON,$\mathrm{S}_1$をショートして,$S_{12}$と$S_{22}$の振幅と位相を測定する |
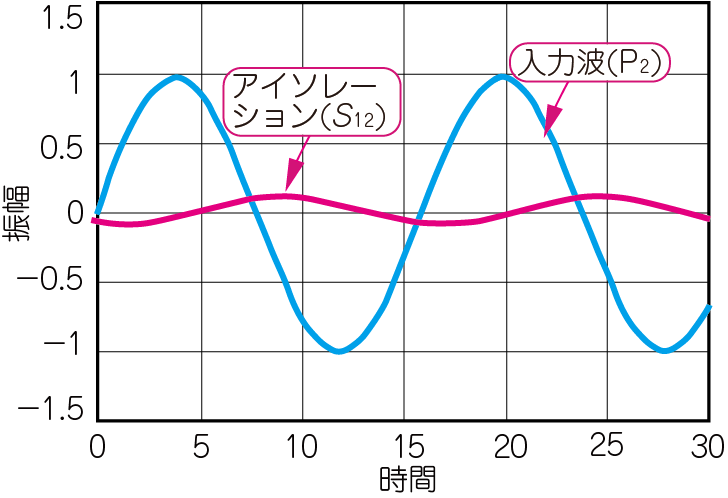
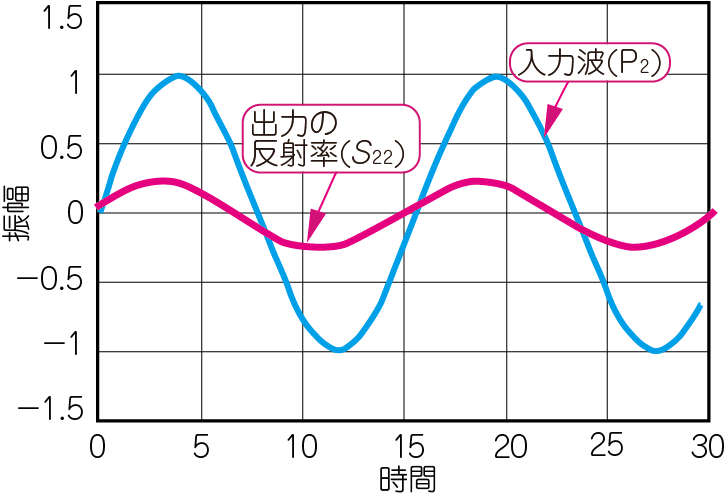
$S_{22}$は,$\mathrm{P}_2$の位置で,不整合による反射波の振幅と位相の比を測ると求まります.$\mathrm{P}_1$の位置で,通過した信号の振幅と位相を測ると,$S_{12}$が求まります.
$S_{22}$と$S_{12}$を測定するときは,$\mathrm{S}_2$を信号源とし,$\mathrm{S}_1$を停止させます(図9).図10に実際に測定した$S_{12}$と$S_{22}$の波形を示します.
3.高周波アンプを評価する
ウェブサイトから$S$パラメータをダウンロードしてシミュレータに組み込む
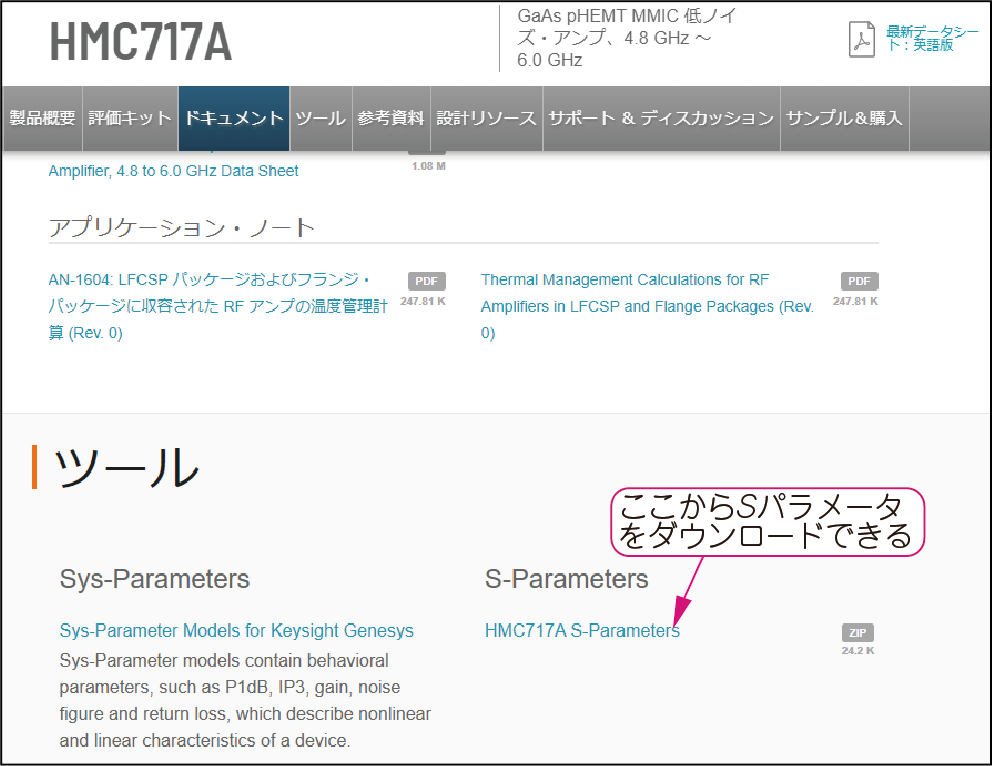
最近のたいていの高周波デバイス・メーカは,ウェブサイトで$S$パラメータを公開しています(図11).
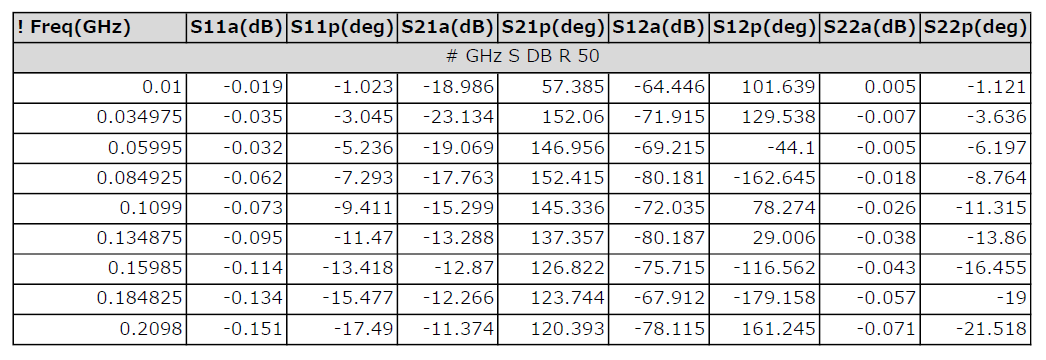
表1に示すのは,HMC717A(アナログ・デバイセズ)という低雑音アンプの$S$パラメータの抜粋です.電源電圧3.0V,$R_{bias}$=5.76kΩ,バイアス電流 29mA,動作温度+25℃の条件下での,さまざまな周波数の$S_{11}$~$S_{22}$の振幅[dB]と位相[°]が示されています.
 |
|---|
| 図11 $S$パラメータは,メーカのウェブサイトからダウンロードできる |
| 低雑音アンプ(LNA,Low Noise Amplifier) HMC717A(アナログ・デバイセズ)の例.今どきは,詳細な$S$パラメータが公開されていないデバイスは敬遠される |
この中から,自分の使用条件に合った$S$パラメータを選び,高周波シミュレータに読み込ませると特性を予測できます.
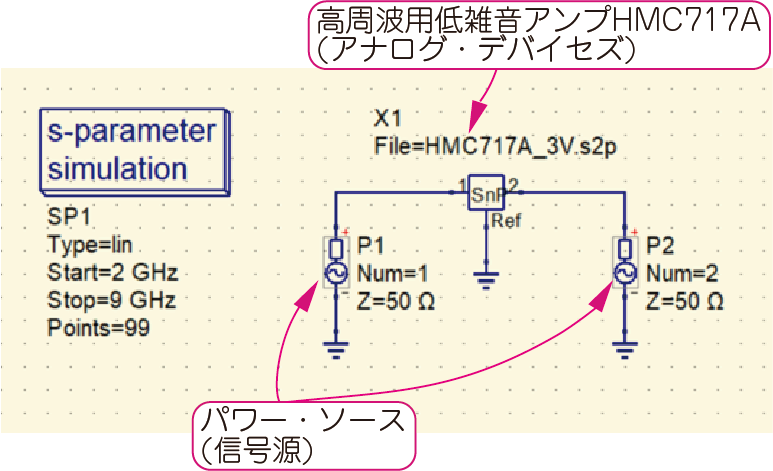
電子回路シミュレータ Qucsを使って,この$S$パラメータを読み込みます(図12).
$\mathrm{S}_1$と$\mathrm{S}_2$用の信号源モデル“Power Source”を2個用意します.
HMC717Aの$S$パラメータは「S parameter file」というコンポーネントを使って設定します.[Parameter File=]で,ファイル名を指定すると,$S$パラメータが読み込まれます.また,“S parameter simulation”で周波数範囲を指定すると,$S$パラメータが表示されます.
 |
|---|
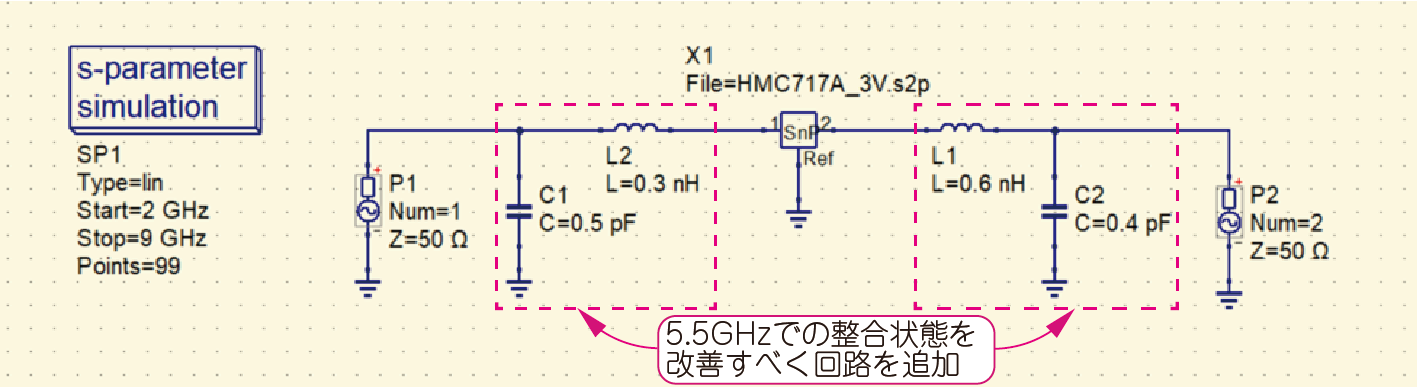
| 図12 高周波アンプ HMC717Aの$S$パラメータを回路シミュレータに入力(整合回路なし) 使用したシミュレータはQucs |
| HMC717Aの裸の特性を確認する.5.5GHzで50Ωに整合して使いたい |
アンプ単体の整合状態
このHMC717Aを5.5GHzで整合させる回路を求めてみます.
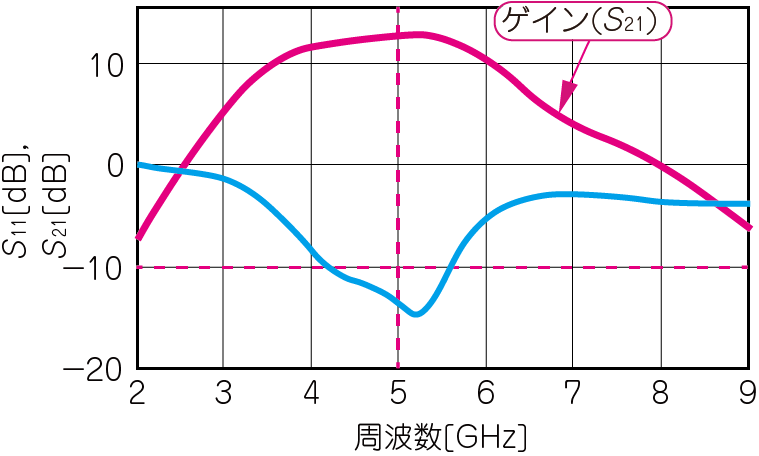
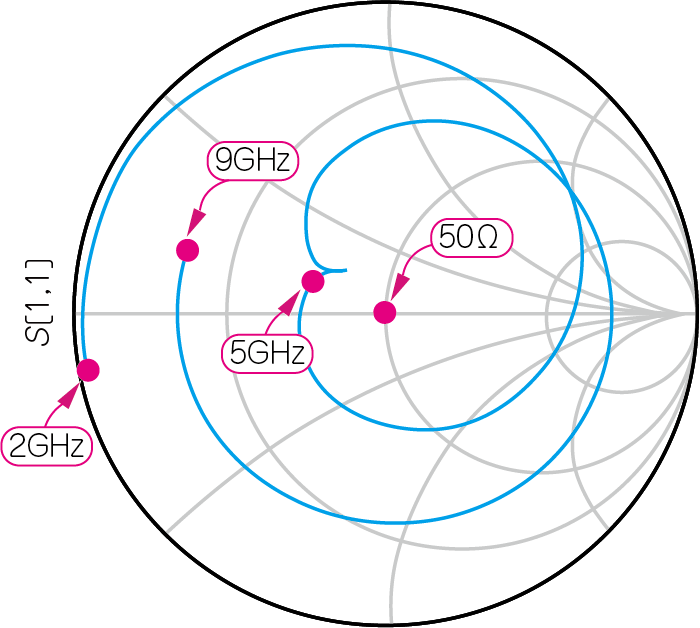
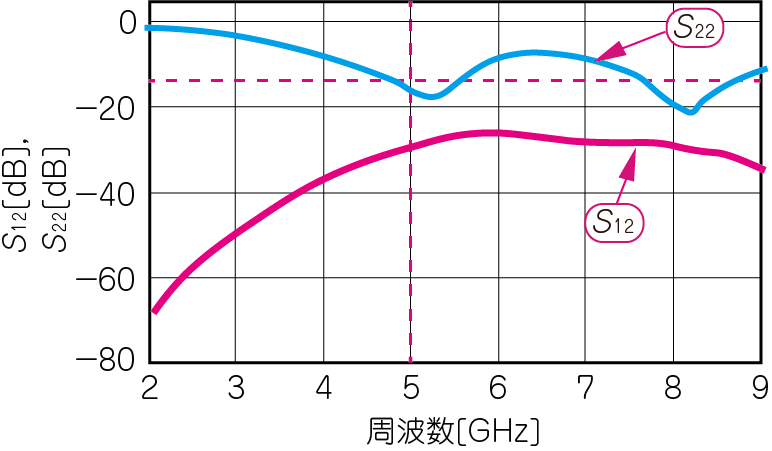
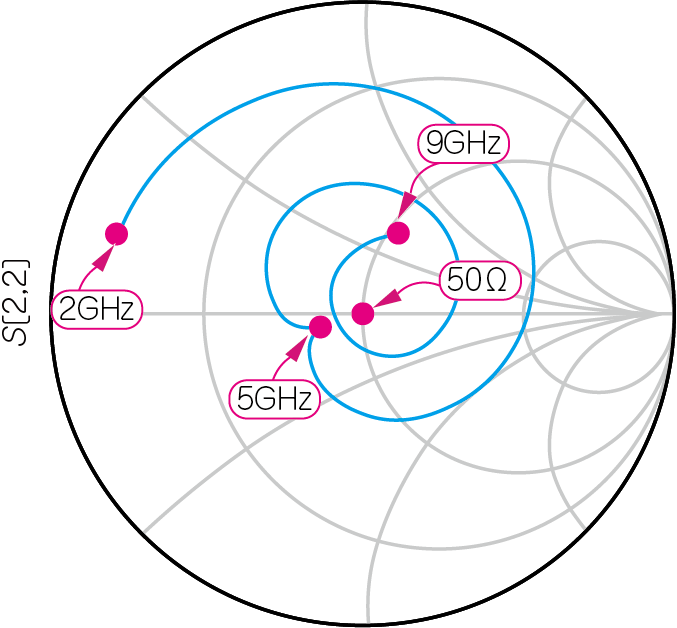
図13と図14に,図12の回路の$S_{11}$,$S_{21}$,$S_{12}$,$S_{22}$をシミュレーションした結果を示します.
反射($S_{11}$や$S_{22}$)は,-10dB以下であれば用途によっては問題にはなりませんから,HMC717Aは,整合回路なしでも5GHz付近でなら使えそうです.
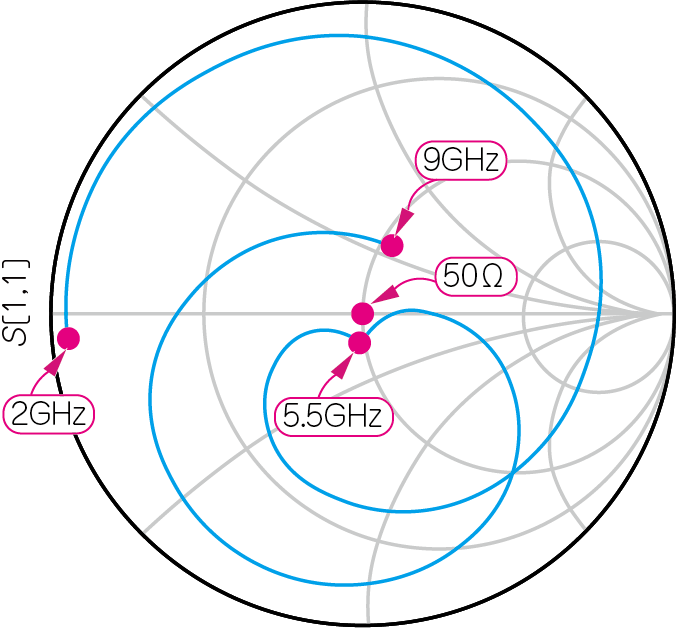
5.5GHzで使おうとすると,反射が悪化し始めるため,改善が必要そうです.図13(b)の5GHz付近のインピーダンス軌跡を右下に動かせば,$S_{11}$は50Ωに近づき整合が改善されます.また図14(b)から,5GHz付近のインピーダンス軌跡を右上に少し移動すれば,$S_{22}$は50Ωに近づき,整合が改善されます.
マッチング回路を追加して整合帯域を広げる
図15に示すのは,HMC717Aの前後にインダクタとキャパシタを追加して,5.5GHzでの整合を改善した回路です.図16と図17にシミュレーション結果を示します.
 |
 |
|---|---|
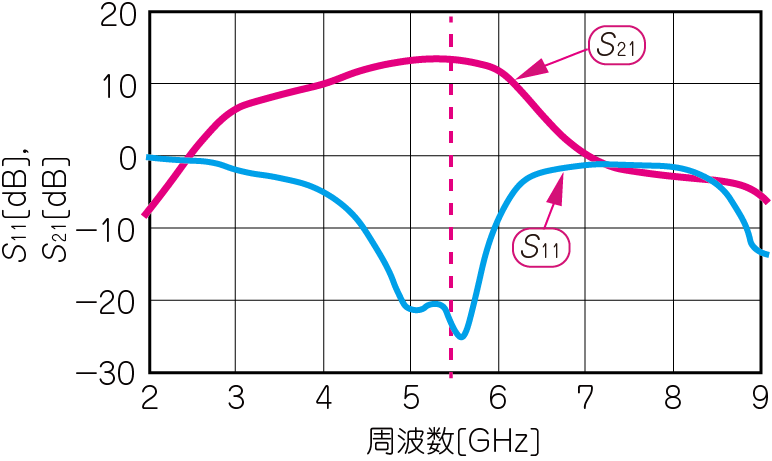
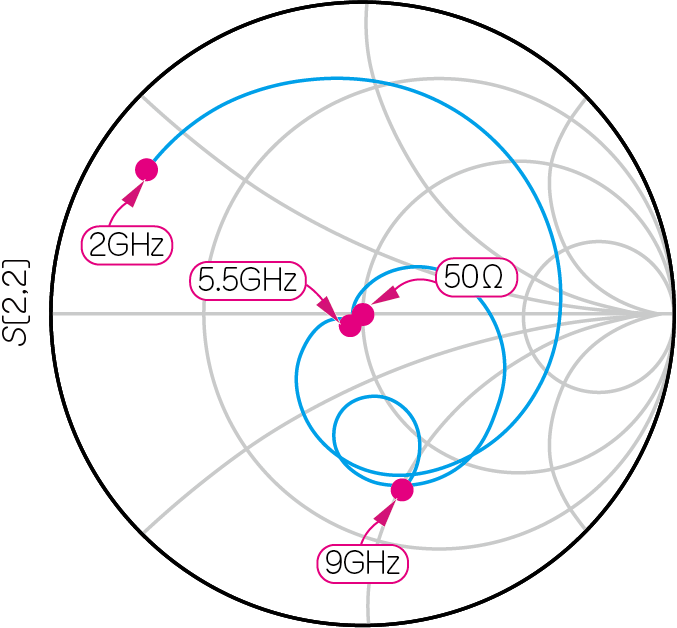
| (a)入力の反射率($S_{11}$)とゲイン($S_{21}$)の周波数特性 | (b)入力の反射率($S_{11}$)のスミス・チャート表現 |
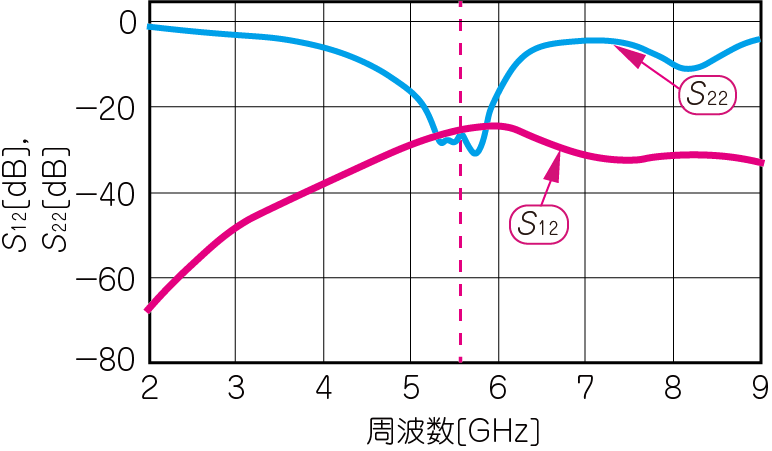
| 図17 図15の回路の$S_{12}$,$S_{22}$の振幅の周波数特性と,整合度を示す目標インピーダンス50Ωと$S_{22}$の位置関係 | |
| $S_{11}$は,5.5GHzを中心に,1GHzの広い周波数範囲において-20dB以下で,整合状態は良好 | |
図16(a)からわかるように,5.5GHz周辺の$S_{11}$は-20dBを下回っています.これは,反射がほぼ存在しないと考えられるレベルです.整合回路の働きによって,図13(a)の$S_{21}$と比べてゲインがフラットな範囲が6GHzまで広がっています.また,図17(a)から,$S_{22}$も5.5GHzを中心に広い範囲で-20dB以下に抑えられています.広い帯域で整合が取れるほど,ばらつきに対するマージンに余裕があり望ましいです.
今回は話を簡単にするため集中定数を使いましたが,実際のGHz帯のRF回路では,定数が極めて小さく寄生成分が目立つため,集中定数で設計すると特性の再現性が良くありません.実際に回路を設計するときは,等価著列抵抗($ESR$,Equivalent Series Resitance)や等価直列インダクタンス($ESL$,Equivalent Series Inductance)などの寄生成分もモデルに含める必要があります.あるいは,マイクロストリップ・ラインを使えば再現性の良いスマートな回路になるでしょう.
4.実測と合うまで!高周波回路はシミュレータで設計する
スミス・チャートを使って手計算や実測で,整合する昔ながらのやり方は,1回で最適な特性を得ることができません.
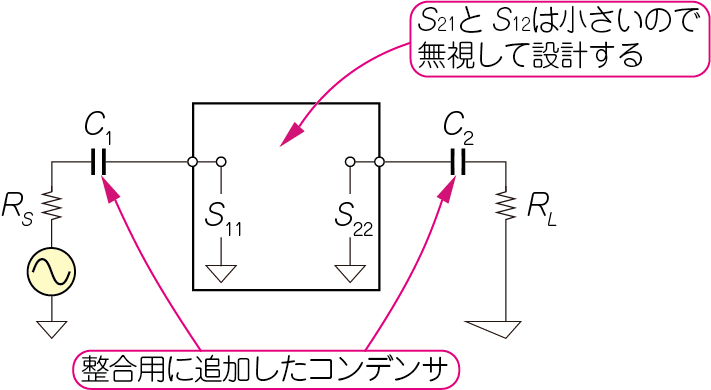
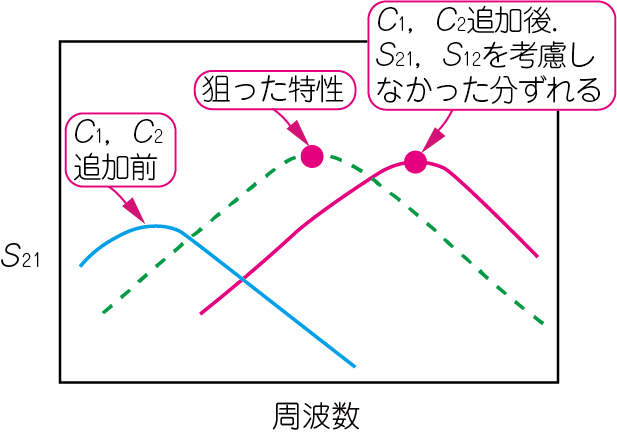
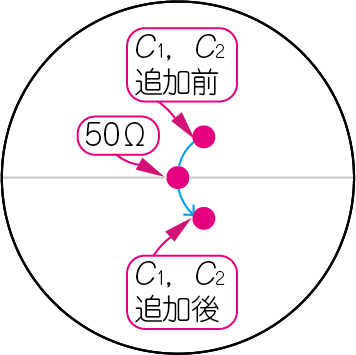
図18に示すように,整合回路の定数を手計算で求めるときは,$S_{11}$と$S_{12}$だけを使います.影響の小さい$S_{21}$と$S_{12}$も含めて計算したいところですが,とても煩雑な作業になるため,これらの影響を無視するのが定石です.しかしその分の誤差が必ず出て,1回目の整合回路では,狙ったポイントから少しずれます.2回,3回と計算をやりなおして微調整する作業が必ず発生します.
高周波シミュレータは,$S_{21}$と$S_{12}$に影響も含めて仕上がりの特性を算出してくれるので,一発で狙いどおりの整合回路を設計することができます.
メーカが公開している$S$パラメータを使ったシミュレーション結果は,周辺回路や伝送路のモデルの精度が高ければ,かなり正確に特性を予測できます.
ただし,シミュレータに頼ってやみくもにカット・アンド・トライを繰り返すと,部品点数が無駄に多い効率の悪い回路ができ上がったり,大きな問題点や最適な答えを見落としたりします.スミス・チャート上で$S$パラメータの軌跡をイメージできるようになることで初めて,早く問題点を見つけ出し,最良の対策を打ち出せるようになるでしょう.
関連製品・記事
- [KIT]ミリ波5G対応アップ・ダウン・コンバータ MkⅡ(mz-mmcon1後継機)
- [KIT]ミリ波5G対応アップ:ダウン・コンバータ(生産終了品)
- [KIT]実験用800M~6GHz 広帯域90°ハイブリッド
- [KIT]実験用27.5G-29.5GHzバンド・パス・フィルタ
- [KIT]実験用28GHzミリ波パッチ・アンテナ
- [VOD/KIT]GPSクロック・ジッタ・クリーナ
- [VOD]MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
- [VOD/KIT]3GHzネットアナ付き!RF回路シミュレーション&設計・測定入門
- [VOD/KIT]3GHzネットアナ付き!初めてのIoT向け基板アンテナ設計
- [VOD/KIT]初めてのソフトウェア無線&信号処理プログラミング 基礎編/応用編
- [VOD]Pythonで学ぶ マクスウェル方程式 【電場編】+【磁場編】
- [VOD]Pythonで学ぶ やりなおし数学塾1【微分・積分】
- [VOD]Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
- 超長距離無線LoRaからローカル5Gまで!GNU Radio×USRPで作るソフトウェア無線機
DTP:ふじむぅスタジオ
(c)Takashi Kato All Right Reserved.
« ZEPマガジン前の記事「5G時代の先進ミリ波ディジタル無線実験室[Vol.5 高周波センスを磨く!スミス・チャート]」
ZEPマガジン次の記事「5G時代の先進ミリ波ディジタル無線実験室[Vol.7 高速データ伝送 成功の鍵「群遅延」]」 »