[技術連載]
5G時代の先進ミリ波ディジタル無線実験室
[Vol.7 高速データ伝送成功の鍵「群遅延」]

次世代高速移動通信と高分解能レーダのキー・テクノロジ

著者・講師：株式会社ラジアン（加藤隆志/Takashi Katou）
企画編集・主催： ZEPエンジニアリング株式会社

関連製品：［KIT］ミリ波5G対応アップ・ダウン・コンバータ MkⅡ（mz-mmcon1後継機）
関連製品：［KIT］ミリ波5G対応アップ：ダウン・コンバータ（生産終了品）
関連製品：［KIT］実験用800M～6GHz 広帯域90°ハイブリッド
関連製品：［KIT］実験用27.5G-29.5GHzバンド・パス・フィルタ
関連製品：［KIT］実験用28GHzミリ波パッチ・アンテナ
関連製品：［VOD/KIT］GPSクロック・ジッタ・クリーナ
関連製品：［VOD］MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
関連製品：［VOD/KIT］3GHzネットアナ付き！RF回路シミュレーション＆設計・測定入門
関連製品：［VOD/KIT］3GHzネットアナ付き！初めてのIoT向け基板アンテナ設計
関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング基礎編/応用編
関連製品：［VOD］Pythonで学ぶマクスウェル方程式【電場編】＋【磁場編】
関連製品：［VOD］Pythonで学ぶやりなおし数学塾1【微分・積分】
関連製品：［VOD］Pythonで学ぶやりなおし数学塾2【フーリエ解析】
関連記事：超長距離無線LoRaからローカル5Gまで！GNU Radio×USRPで作るソフトウェア無線機

【Index】

超低$C/N$！mz-mmcon1 後継機 z-mmcon2 誕生

写真Aに示すのは，1台でミリ波を使ったディジタル無線通信が可能な$I/Q$変調＆周波数コンバータ“z-mmcon2”(開発：ラジアン)です．ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1の後継機です．


写真A　1台でローカル5Gのミリ波無線通信の実験が可能なアップ・ダウン・コンバータ z-mmcon2（mz-mmcon1のC/Nを大幅に改善した後継機 (開発：株式会社ラジアン）

スペック

送信周波数範囲：24.0G～44.0GHz
送信出力範囲：+10～-29dBm（信号の条件 CW）
送信ゲイン範囲：+20～-19dB（$I/Q$動作時）
受信周波数範囲：24.0G～44.0GHz
受信入力範囲-：10dBm以下（信号の条件 CW）
受信ゲイン範囲：+12～-9dB（$I/Q$動作時）
受信雑音指数：10dB以下
ベースバンド周波数範囲：DC～100kHz（内蔵D-Aコンバータ，外部アクセス不可）
ベースバンド・レベル範囲：0dBm以下（内蔵D-Aコンバータ，外部アクセス不可）
IF周波数範囲：1G～6GHz（本体背面のSMA端子）
IFレベル範囲：0dBm以下（本体背面のSMA端子）
電源：付属のACアダプタ（DC6V，2A）
消費電流：1.5A（通常動作時）
基板サイズ：128×93×1.6mm（基材はRogers4350B）
ケース・サイズ：$W$=140mm $D$=129mm $H$=40mm（フランジ含む）

従来品ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1からの改善点

z-mmcon2（写真A ）は，従来機のmz-mmcon1から，下記の点が改良されています．

周波数範囲の拡大（27GHz～43GHz → 24GHz～44GHz）
シンセサイザICの変更（ADF4372）に伴う$C/N$の大幅改善
制御をWindowsアプリからターミナルに変更（FTDIドライバに起因するトラブル回避）
外部機器との接続をIF（1G～6GHz）だけに変更
放熱ケース採用とファンレス化，ケースの大型化
USBマイクロをUSB-Bに変更（コネクタ破壊対策）

波形品質を決めるハードウェア性能「群遅延」

次世代5G通信システムの本命，28GHzミリ波通信のベースバンド信号の帯域は400MHzあります．このように広い帯域の周波数成分で構成される信号の波形を乱すことなく伝送することが，低エラーレートかつ伝送速度の高速化に欠かせません．

今回は，フィルタの伝送路の良し悪しを判断する指標「群遅延」の意味やシミュレーション解析の方法を紹介します．全周波数成分の遅延時間が一定の，すなわち群遅延一定の伝送路や回路を設計することが，400MHzというこれまでにない超広帯域通信に成功するかぎです．

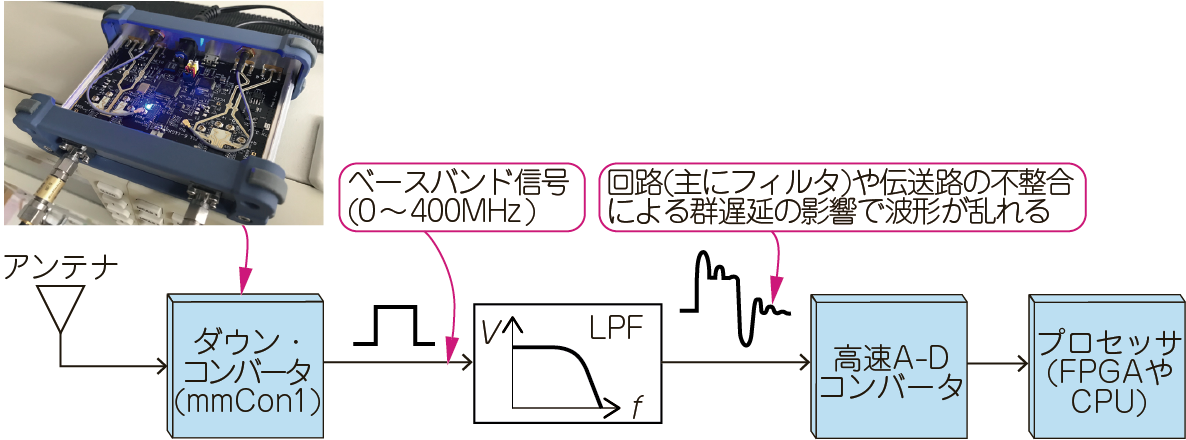
主に，LPFの位相変化が，群遅延特性を悪化させます(図1)．逆にこれらの群遅延の総合特性が実用的な帯域を決定します．〈ZEPエンジニアリング〉


図1　高速通信システムを設計するときは，不整合部(基板のビアなど)やLPFなど，広帯域信号の波形を乱す箇所を把握して対処する必要がある

広帯域伝送性能が求められる高速通信機の性能指標「群遅延」

今回のねらい

本連載 Vol.5とVol.6では，「スミス・チャート」や「$S$パラメータ」という便利なツールを利用して，高周波回路のインピーダンス整合などを設計しました．このときは「振幅」と「位相」の2つのパラメータを使いました．

しかし，400MHzという広い帯域の周波数成分で構成された信号の波形を変化させず伝送するディジタル変調では，この2つのテクニックでは不足です．加えて「群遅延」という指標を使って，伝送路や回路を評価する必要があります．

今回は，広帯域信号を伝送する線路の位相遅延と群遅延，波形ひずみの関係を整理します．

広帯域という言葉の整理

「広帯域」という言葉は，2つの意味で使われています．1つは，単に周波数が広いと意味です．

2つ目は「比帯域が大きい」ということです．本質的にはこちらの意味で広帯域という言葉を使うほうがよいと思います．比帯域($k_B$)とは，キャリアの中心周波数($f_0$)と通信帯域($f_{BW}$)の比です．式で表すと次のようになります．

\begin{equation} k_B=\frac{f_{BW}}{f_0} \end{equation}

本稿では，3オクターブ以上を「広帯域」と定義します．

ミリ波5Gのキャリアの中心周波数は28GHz，帯域は400MHzです．400MHzは，一般的に見て相当に広い帯域ですが，比帯域は他の通信規格と同程度です．ただし，ベースバンドは，$f_B$(Low IFのセンタ周波数)±200MHzなので超広帯域信号として扱います．

ディジタル回路でおなじみの“1”と“0”のデータ信号は広帯域信号

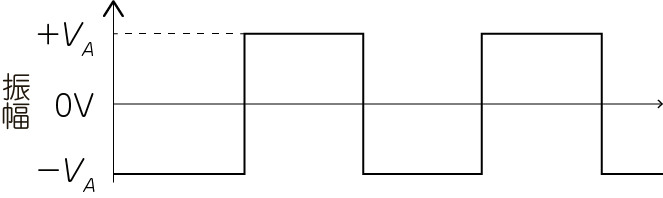
正弦波の周波数は単一です．一方，図2に示す矩形波は，周波数の異なる(奇数次)多くの一周波数の正弦波がたくさん足し合わされてできています．つまり，広い帯域にわたる信号を含んでいます．


図2　ディジタル回路で扱うデータ信号は広帯域信号
通信の高速化には，ディジタル信号の波形が乱れない伝送路の設計技術が必要

式で表すと次のようになります．

\begin{equation} y(t)=\frac{4A}{\pi} \left[ \sin(\omega t) + \frac{1}{3} \sin(3 \omega t) \frac{1}{5} \sin(5 \omega t) + \cdots \right] \end{equation}

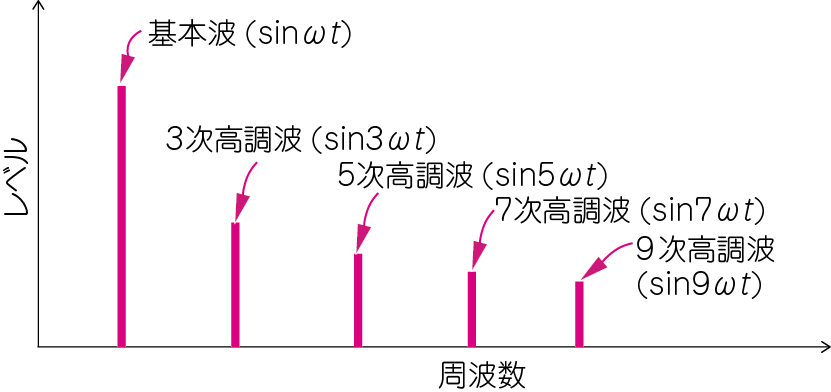
この式は「位相の揃った奇数次高調波を加算すると矩形波になる」と言っています．逆に，矩形波をスペクトルに分解すると，図3のようになります．


図3　矩形波はたくさんの単一周波数正弦波で構成された広帯域信号である

矩形波は，見慣れたデータ信号の波形です．高調波を含んだとても帯域の広い信号なので，伝送路や回路を通過するうちに，特に周波数の高い成分の遅延が変化したり減衰したりして波形が乱れてきます．

すべての周波数成分を遅延時間一定で伝送したい

周波数成分によって遅延量が同じなら波形は保たれる

矩形波を用意する

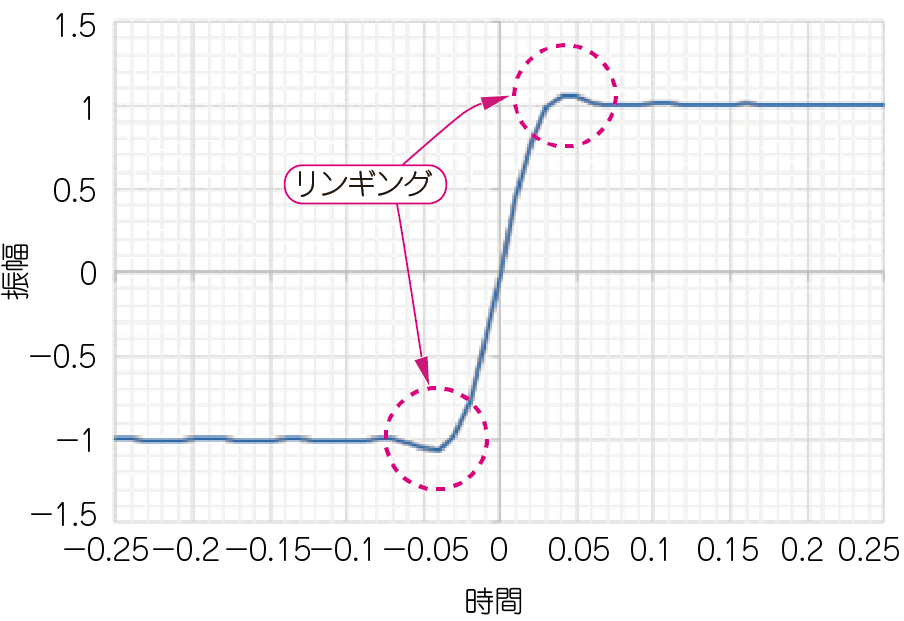
図4(a)に示すのは，式(2)を使って，15次高調波までの単一周波数の正弦波を足し合わせた波形です．この波形は，矩形波をLPFに通して15次以上の高調波を取り除いたものです．

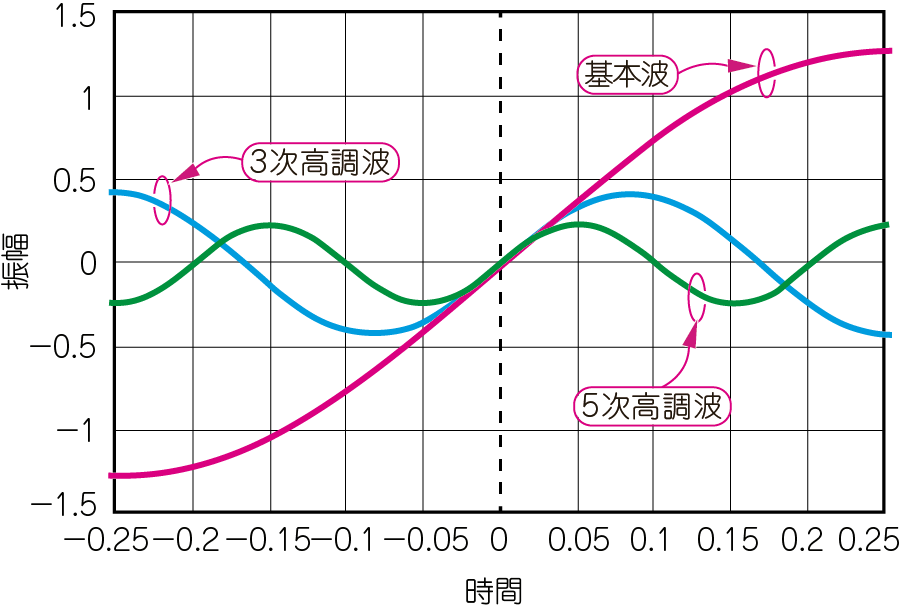
図4(b)に示すのは，この矩形波を構成する単一周波数の正弦波(1次，3次，5次)に分解した波形群です．見やすくするために5次までを表示しました．いずれの波形も，時間0を起点にして変化しており，位相が揃っています．


(a)1～15次の周波数成分を足し合わせた波形	(b)図(a)の矩形波を構成する単一周波数の正弦波群(5次以下の高調波だけを表示)
図4　15次高調波までの単一周波数の正弦波を足し合わせた波形
Excelに式(2)を入力して，15次高調波まで計算．横軸の1は基本波の周期を正規化した値．基本波が1GHzの場合は，±1は±0.25nsを意味する

群遅延一定の伝送路を通過させてみる

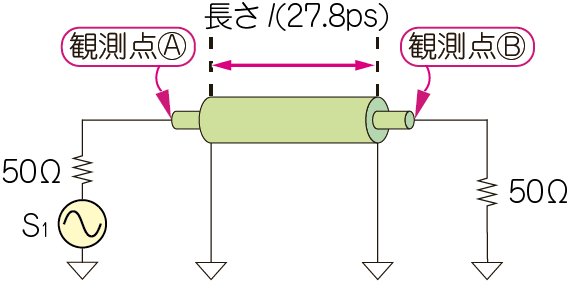
この矩形波を図5に示す伝送路に通します．この伝送路は，送信インピーダンス，受信インピーダンス，そして伝送路の特性インピーダンスはすべて50Ωです．広帯域信号を入力すると，そのまま周波数特性がフラットな状態で通過します．


図5　$Z_0$=50Ω，遅延時間27.8psの伝送路

一般に伝送路の長さは遅延時間で表します．

この伝送路の長さは27.8psです．この伝送路を通過するのに，どんな周波数も27.8ps要します．

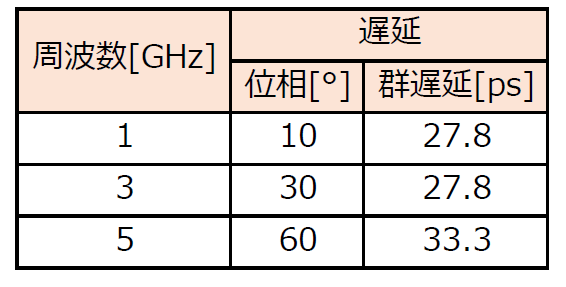
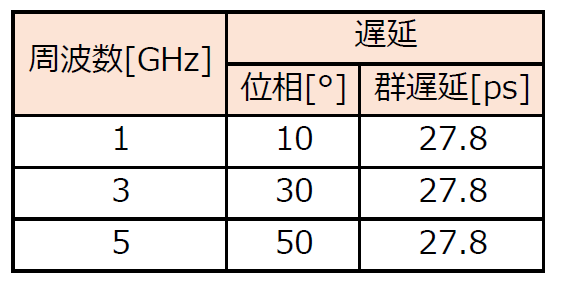
27.8psを位相[°]で表すと，1GHzの正弦波の場合「10°の遅れ」です．物理的な長さ($l$)でいうと，比誘電率$\varepsilon_r=$1(空気)のとき約8.3mmです．3次高調波(3GHz)の遅れは30°，5次高調波(5GHz)の遅れは50°です(表1)．


表1　図5の伝送路に1GHz，3GHz，5GHzを入力したときの遅延量
1GHzを入力すると，位相で10°，時間で27.8ps遅れて出力される．3GHzを入力すると位相で30°，時間で27.8ps遅れて出力される

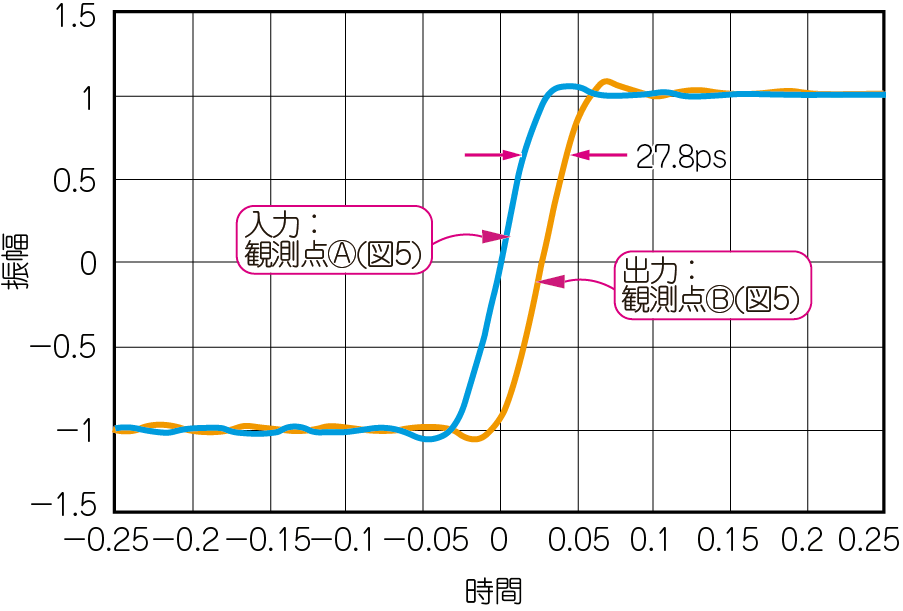
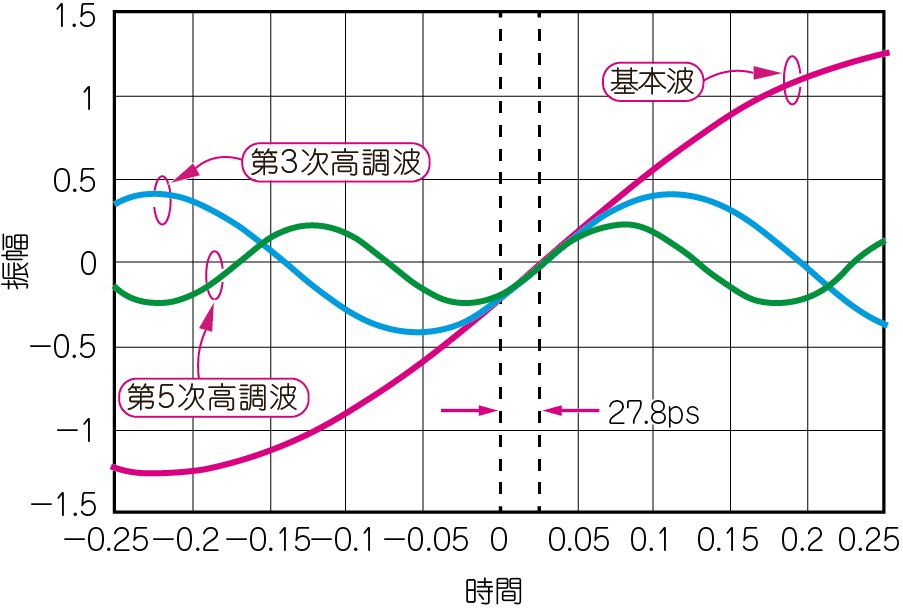
図6(a)に示すのは，図4の矩形波をこの伝送路に入力したときの応答です．27.8ps遅延していますが，波形はきれいに保たれています．図6(b)に示すのは，図6(a)の波形を周波数分解した単一周波数の正弦波群です．全体的に27.8psだけオフセットしていますが，各正弦波の相対的な位相関係は図4(b)と同じです．


(a)1～15次の周波数成分を足し合わせた波形	(b)図(a)の矩形波を構成する単一周波数の正弦波群(5次以下の高調波だけを表示)
図6　矩形波(図4)を図5の伝送路に入力したときの応答波形

群遅延一定の線路は波形を乱さない

群遅延とは，周波数によって変化する位相を微分したものです．式で表すと次のようになります．

\begin{equation} \tau_g==-\frac{d\phi}{d\omega}=-\frac{\Delta \phi}{\Delta \omega} \end{equation}

周波数による位相の変化(相遅延という)が1次関数的なら，群遅延は一定の値を取ります．

表1に示した群遅延は全て同じ値になります．このとき波形はひずまず，図6のような遅延だけが起こります．

周波数成分によって遅延量が違うと波形が乱れる

周波数による遅延量が一定でない伝送線路は矩形波をひずませる

次に，表2に示すように，位相遅延が1次関数的に変化しない伝送路を用意します．1～3次高調波の位相は1次関数的に，3～15次高調波の位相は2次関数的に変化させます．


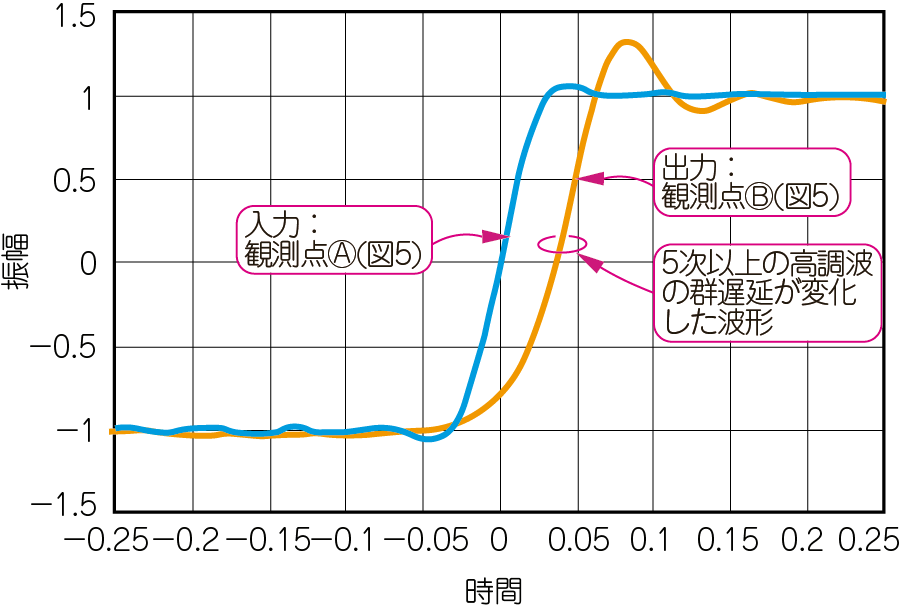
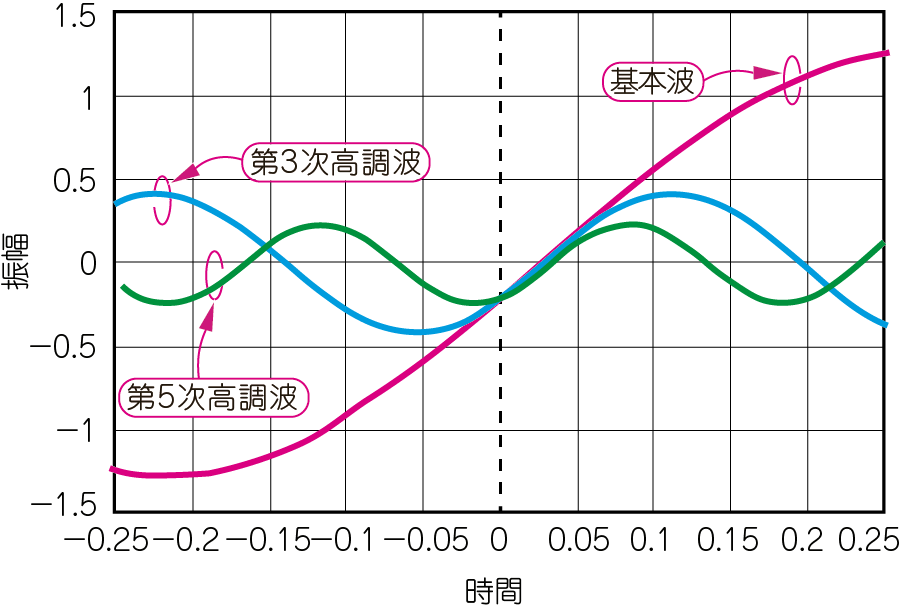
表2　1～3次高調波の位相は1次関数的に，3～15次高調波の位相は2次関数的に変化させる伝送路を用意して，矩形波を入力してみる
図5の伝送路の群遅延特性を変える

この伝送路に，同じく図4の矩形波を入力すると，伝送路の出口(図5の観測点B)の信号の波形が，図7(a)のように大きくひずみます．図7(b)は周波数成分に分解した結果です．5次高調波の遅延が，基本波と3次高調波よりも大きいことがわかります．


(a)1～15次の周波数成分を足し合わせた波形	(b)図(a)の矩形波を構成する単一周波数の正弦波群(5次以下の高調波だけを表示)
図7　表2の伝送路に，矩形波(図4)を入力すると大きくひずむ
Excelに式(2)を入力して，15次高調波まで計算．横軸の1は基本波の周期を正規化した値．基本波が1GHzの場合は，±1は，±0.25nsを意味する

以上のように群遅延が一定の値を取らない周波数域に信号を通すと，波形がひずみます．

このような伝送線路にディジタル信号が通過すると，アイ開口が狭くなって，ビットエラー率($BER$，Bit Error Rate)が悪化し，復調後のシンボルの位置ずれ「エラー・ベクトル振幅($EVM$，Error Vector Magnitude)」が大きくなり，高速通信は望めなくなります．

優れた広帯域伝送路は，周波数によらず群遅延の値が一定なのです．

なお，伝送路ではなく，回路が大きな群遅延の悪化要因になることがよくあります．特にアナログ・フィルタは，カットオフ周波数付近で大きく群遅延を変化させます．精度の高い波形が要求されるときは，信号帯域とカットオフ周波数を離したり，群遅延特性に優れるベッセル・フィルタを採用する例もあります．

まとめ：矩形波がひずむかどうかの重要な指標「群遅延」

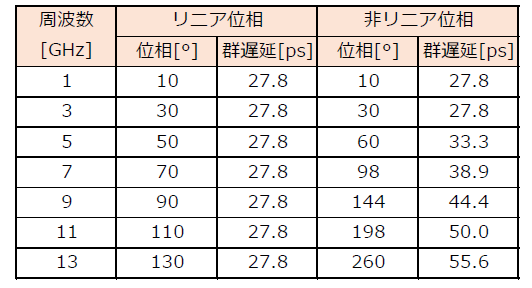
表3に示すように，

1次関数的に位相遅延が変化するリニア位相タイプ
1～3次高調波の位相は1次関数的に変化するが，3次以上の高調波の位相は2次関数的に変化する非リニア位相タイプ

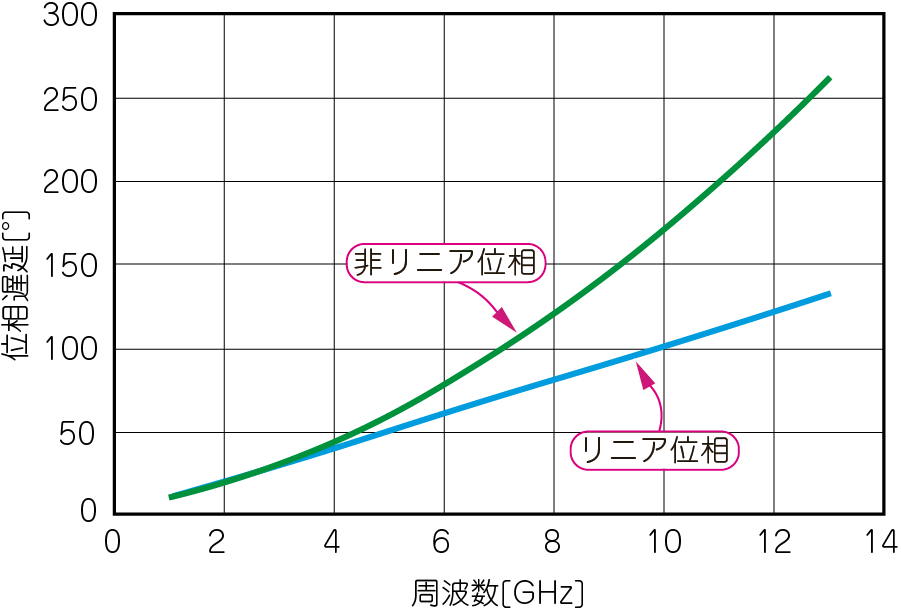
の2つの伝送路を用意します．図8に示すのは，これらの伝送路の周波数応答をグラフで表したものです．


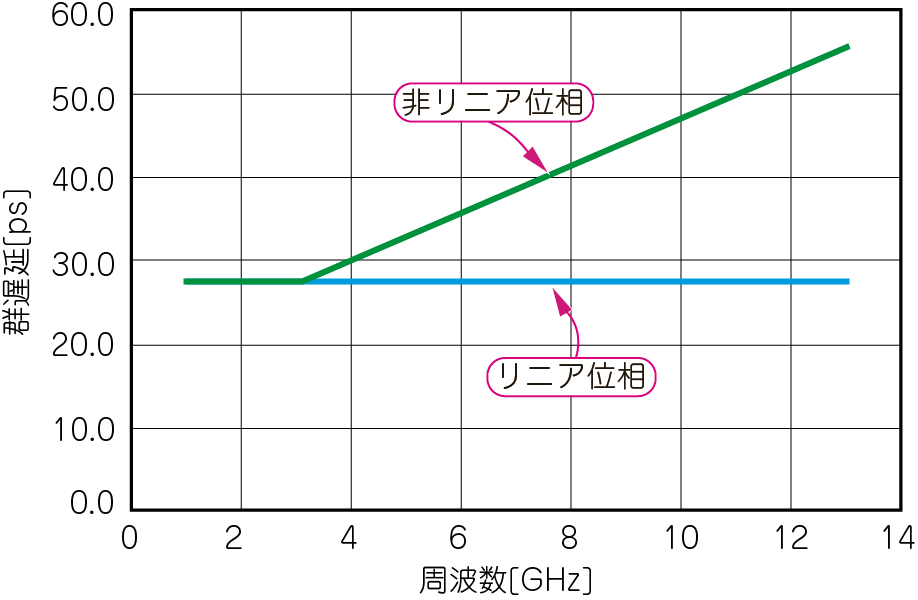
表3　位相遅延を1次関数的に変化させる伝送路と，3次以上で2次関数的に変化させる伝送路があったとする


(a)縦軸を位相遅延[°]とする	(b)縦軸を群遅延（位相遅延の微分)[ps]とする
図8　表3の2つの伝送路の遅延特性をグラフ化するとこうなる
図(b)の表現法のほうが，波形への影響の度合いを判断しやすい

縦軸が位相遅延の図8(a)からは，何次の高調波から波形ひずみに影響するのかはっきりと判別できませんが，縦軸が群遅延の図8(b)からは，3次(3GHz)以上の高調波がひずみに影響を与えることが明示的です．

特に，位相回転が大きい長い伝送路や大規模回路では，リニア位相と非リニア位相を区別しにくくなりますから，相遅延ではなく群遅延を利用価値を感じるでしょう．

メーカ製LPFの群遅延を評価してみる

遅延の周波数特性をシミュレータで解析

メーカから$S$パラメータをダウンロード

デバイスの群遅延は，ネットワーク・アナライザで測定したり，デバイス・メーカが公開している$S$パラメータから算出することができます．実際にやってみましょう．

高周波回路も解析できるフリーのアナログ電子回路シミュレータ“Qucs Studio”を使って市販フィルタの群遅延特性を求めてみます．

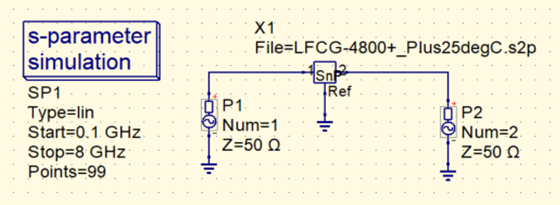
図9に示す2ポートのシミュレーション回路を用意します．次のウェブサイトから表面実装型のチップLPF(LFCG-4800+，ミニサーキッツ製)の$S$パラメータをダウンロードします．

https://www.minicircuits.com/WebStore/dashboard.html?model=LFCG-4800%2B


図9　電子回路シミュレータを使って，実際のデバイス(LFCG-4800+)の群遅延特性を解析してみる

位相遅延の周波数応答

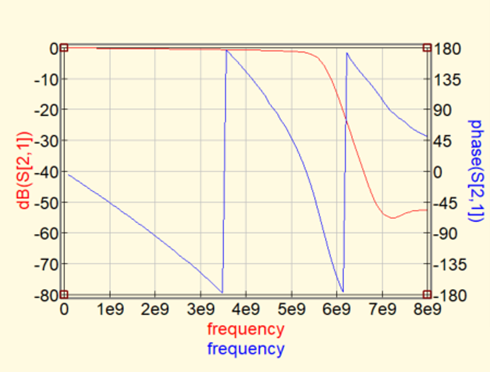
図10に示すのは，LFCG-4800+の通過特性($S_{21}$)の振幅と位相を計算した結果です．


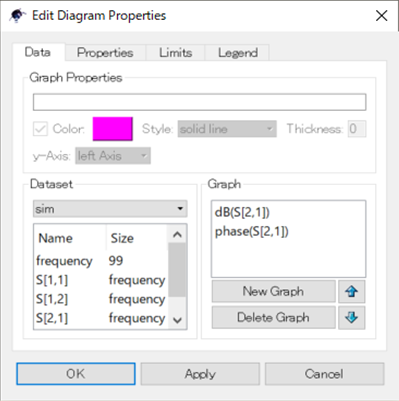
(a)$S_{21}$のゲインと位相の周波数特性	(b)シミュレーションの設定
図10　図9の回路のゲインと位相の周波数特性(縦軸は位相[°])
5G～6GHzの部分で位相の回転が激しくなっているが，何Hz以下なら問題ないかを判断するのは難しい

カットオフ周波数(5.5GHz)付近で位相の変化が激しくなり，傾きが急峻になっています．このグラフからは，このLPFがどの周波数まで使えるのかを判断できません．

図10(a)に示すように，縦軸を位相にするグラフが有効なのは，周波数による位相の変化が小さい応用です．例えば次のような場合です．

差動トランス(バランなど)の位相差が180°確保できる周波数範囲を確認したい
アンプの入出力位相差を確認したい

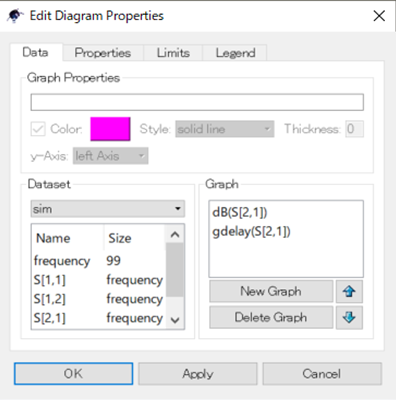
Qucsで振幅と位相を表示させるためには，Edit Diagram Propatiesで次のように記述します[図10(b)]．

振幅：dB(S[2,1])
位相：phase(S[2,1])

群遅延の周波数応答

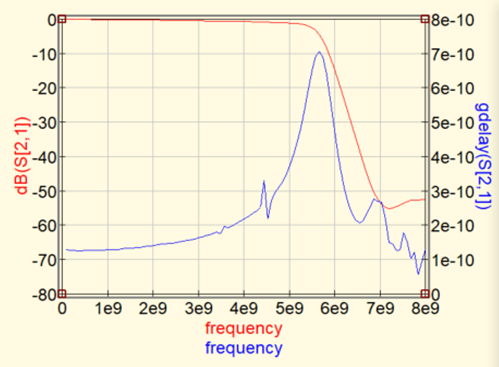
図10の縦軸の設定を群遅延に変更すると，図11(a)のようなグラフが表示されます．


(a)$S_{21}$のゲインと位相の周波数特性	(b)シミュレーションの設定
図11　図9の回路のゲインと位相の周波数特性(縦軸は群遅延[ps]
何Hzまで使えそうか判断がしやすい

振幅と位相を表示させるためには，Edit Diagram Propatiesで次のように記述します．

振幅：dB(S[2,1])
位相：gdelay(S[2,1])

このグラフから，広帯域信号がひずみなく通せる範囲はだいたい4GHz以下と判断できます．許容できる群遅延は，求められる波形の精度によります．

なお，4GHz以下の10nsの群遅延が問題になる場合は，この部分は経時変化が少ないと仮定して，信号処理で補正をかけるとよいでしょう．ただし，個体ばらつきや経時変化の影響を受けるLPFのカットオフ周波数付近の位相変化は，信号処理による補正でも対処できないでしょう．カットオフ周波数と信号帯域をできるだけ離すしか対策はありません．

Excelに計算式を入れて$S$パラメータから群遅延を求めると同じ結果が得られる

図9～図11では，LFCG-4800+の$S$パラメータから群遅延を算出する処理を電子回路シミュレータQucsに任せました．ここでは，$S$パラメータから群遅延を手計算で算出してみます．

メーカのサイトからダウンロードされる$S$パラメータは，テキスト・ファイルです．これをExcelに読み込んで，次式を使って群遅延を求めてみます．

\begin{equation} H =2\pi f_n \end{equation} \begin{equation} \Delta\theta = \frac{\pi}{180} \left( \theta_{n+1} - \theta_n \right) \end{equation} \begin{equation} \Delta \omega = \omega_{n+1} - \omega_n \end{equation} \begin{equation} \tau_g = \frac{\Delta \theta}{\Delta \omega} \end{equation}

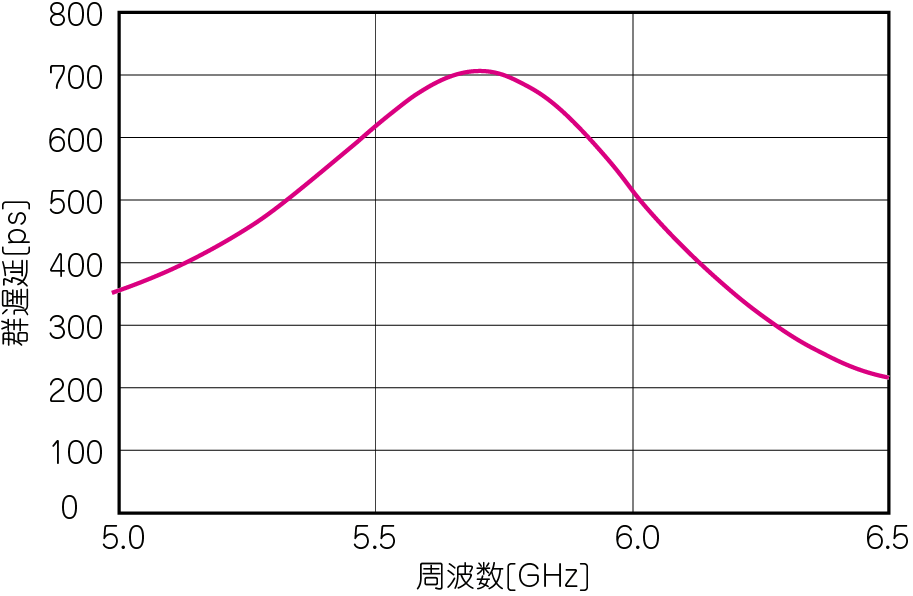
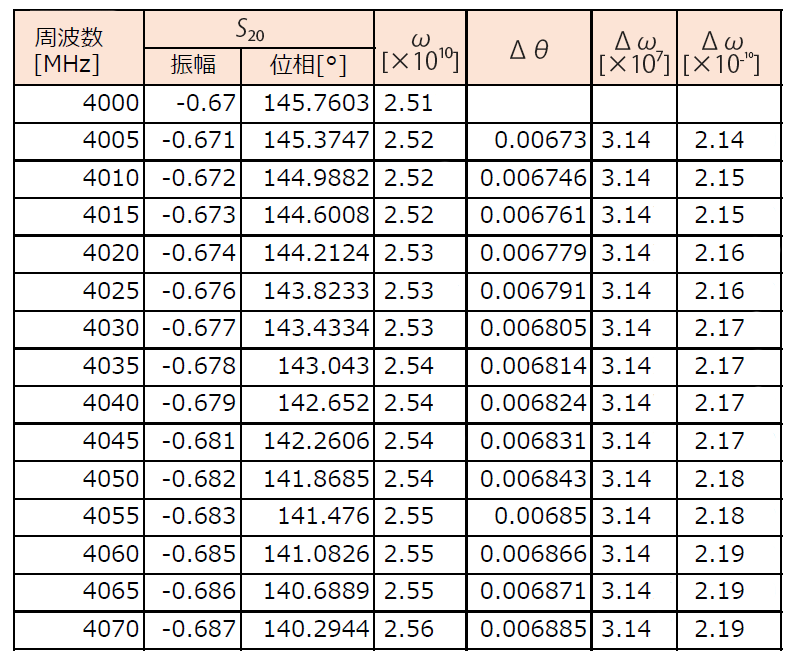
表4に計算の一部を抜粋して示します．$S_{21}$の振幅と位相は$S$パラメータの値そのままです．図12に示すのは，LFCG-4800+のカットオフ周波数付近(5G～6.5GHz)の群遅延の周波数応答です．図11(a)と見比べてみてください．同じ結果が得られています．


表4　メーカ製LPF(LFCG-4800+)の$S$パラメータ・ファイル(テキスト・データ)からExcelを使って群遅延を算出してみた
ダウンロードした$S$パラメータから得られる「振幅」と「位相」から群遅延を求める


図12　表4のデータをグラフ表示すると図11(a)と同じ結果が得られる

コラム
オーディオ・アンプの周波数特性は振幅だけじゃない

今回紹介した，矩形波を使った群遅延の評価方法は，高周波回路だけでなく多くの電子回路の広帯域の周波数応答を調べるのに有効です．例えば，アクティブ電源の負荷に矩形波状の電流負荷を与えると，その出力電圧波形から応答性能を評価できます．リンギングの発生状況から位相余裕や収束時間など，多くの情報が得られます．

オーディオ・アンプの性能を正確に評価したいならば，振幅だけでなく群遅延の周波数応答も測定すべきでしょう．アンプに矩形波を加え，抵抗性や誘導性の負荷をかけて出力波形を観測して，振幅の周波数特性以外に，群遅延による応答性能を調べます．周波数によって遅延時間に差があれば，耳に聞こえる音色にも変化があると予想されます．

なお，群遅延だけでなく，振幅の周波数特性も矩形波の波形ひずみに影響することは，本連載第4回のコラムで解説ずみです．〈加藤隆志〉

コラム
アナログの限界をディジタルで克服！
広帯域ディジタル変調技術“OFDM”

本文で解説したように，周波数によって群遅延が変化すると，波形がひずみます．このことから，帯域の広いディジタル信号の波形を保って伝送するのは至難の業であることがわかります．

ディジタル通信システムの中の群遅延を変化させる主要因は，帯域制限のためのアナログ・フィルタです．キレの良い多段フィルタほど大きな群遅延を発生させます．

同じフィルタでも，通信の帯域自体が狭ければ群遅延の変化は小さくなります．直交周波数分割多重(OFDM，Orthogonal Frequency Division Multiplexing)通信方式は，狭帯域の信号(サブキャリア)をびっしり周波数方向に並べて広帯域化したものです．各サブキャリアは狭帯域なので，各サブキャリア単体で見たら群遅延の変化が小さくなります．

400MHzの帯域を実現するミリ波5G通信や帯域528MHzのUWB(Ultra Wide Band)通信では，アナログ回路の制約を受けずに広帯域化できるOFDM方式を採用しています．

多数の狭帯域サブキャリアをリアルタイムに信号処理するためには，超高速ASIC(Application Specific Integrated Circuit)やFPGA(Field-Programmable Gate Array)を使ったSDR(Software Defined Radio)技術が必須です．OFDMは，デバイスの進化によって実現できるようになった技術といえるでしょう．〈加藤隆志〉

[技術連載] 5G時代の先進ミリ波ディジタル無線実験室 [Vol.7 高速データ伝送 成功の鍵「群遅延」]